Bootstrap Your Own Latent: A New Approach to Self-Supervised Learning(2020)

관련 링크 : https://arxiv.org/abs/2006.07733

딥러닝을 이용한 컴퓨터 비전 분야에서, 어떤 종류의 Task에서도 좋은 성능을 발휘하는 Representation을 내놓는 모델을 찾는것은 중요하다. Self-Supervised Learning은 이와 관련된 가장 촉망받는 분야 중 하나로, 최근까지도 활발히 연구되고 있다. 오늘 이야기 할 논문은 이런 SSL 방법 중 하나로, Self-Training과 Self-Supervised Learning을 러프하게 결합한 듯 보이는 BYOL(Bootstrap Your Own Latent)를 제안한다.

위 성능 그래프를 살펴보면, 이전 SSL 방법들과 비교해 봐도 압도적인 성능을 보이면서 Supervised Learning에 거의 근접한 성능을 보인다. 그럼 BYOL에 대해 알아보자.

Bootstrap Your Own Latent

최신 연구들은 공통적으로 한 이미지의 여러 변형된 형태들은 유사한 Representation을 가진다고 생각하고 이미지들을 이용해 Representation을 예측하도록 모델을 학습시킨다. 하지만 다른 이미지들과의 비교 없이 한 이미지의 변형된 형태들(Positive Pairs)만 고려한다면, 모델은 모든 이미지들을 하나의 representation으로 예측해 버릴 것이다. 따라서 대부분의 연구들은 많은 수의 다른 이미지들(Negative Pairs)을 이용해 위의 예측 문제를 두 Pairs들의 차이를 구별하는 문제로 우회시킨다. 이때 Negative Pairs는 보통 Batch에서 가져오거나 별도의 Memory Bank를 만들어서 보관하는데, 문제의 난이도를 높이는 Negative Pairs이지만 의미상으로 같은 이미지들이 학습에 포함되도록 Negative Pairs의 크기를 가능한 키워준다.

하지만, BYOL는 기존 최신 방법들과 달리 Negative Pairs를 사용하지 않는다. 그 대신에 매우 천천히 변하는 Target Network와 BackProp을 통해 학습되는 Online Network를 이용한다. 학습 방법은 다음 그림과 같다.

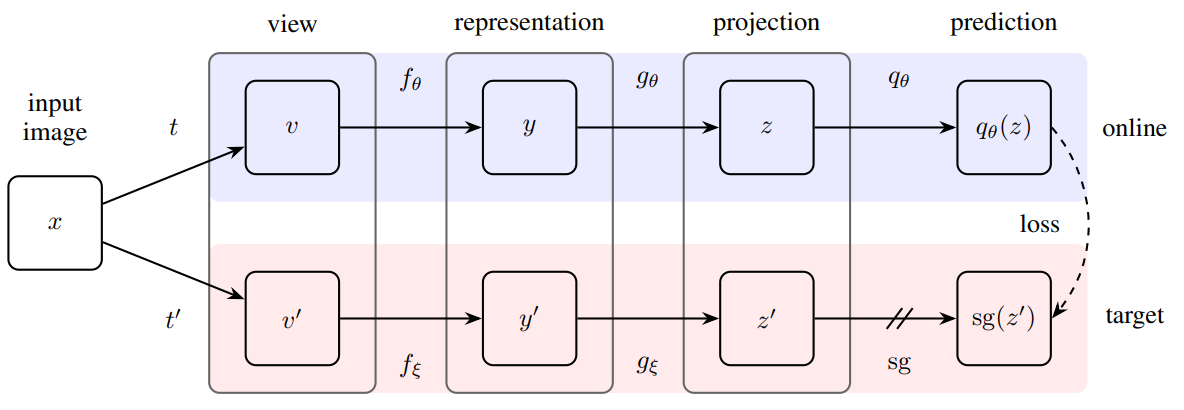
1. 먼저 입력 이미지를 Augmentation $t$, $t’$를 통해 $v$, $v’$을 얻는다.

2. 이를 동일한 구조를 가진 모델에 넣어 $z$, $z’$를 얻는다.

   이때 Online의 파라미터는 $\theta$, Target은 $\xi$이다. $\mathrm{sg}$는 Stop Gradient를 뜻하고, Target은 학습이 되지 않음을 의미한다.

3. $z$를 predictor $q_\theta$에 넣어 $q_\theta(z)$를 얻고, $z’$와 MSE Loss $\mathcal{L}{}^\mathrm{BYOL}_\theta$를 계산한다.

4. $v$와 $v'$를 바꿔서 2-3을 수행해 $\mathcal{\overset{\sim}{L}}{}^\mathrm{BYOL}_\theta$, $\mathcal{L}{}^\mathrm{BYOL}_\theta+\mathcal{\overset{\sim}{L}}{}^\mathrm{BYOL}_\theta$를 구한다.

5. Loss를 이용해 Online Network를 학습시키고, Target Network는 $\theta$를 이용해 업데이트한다.

   $\xi$는 Online 파라미터 $\theta$의 지수 이동 평균으로 $\xi\leftarrow \tau\xi+(1-\tau)\theta$를 이용해 업데이트한다. 이때 $\tau \in[0,1]$이다.

6. 위 과정을 반복(Bootstrap)하고, 학습이 끝나면 최종적으로 $f_\theta$를 제외한 나머지는 제거한다.

BYOL은 왜 성능이 좋을까?

그런데, 왜 BYOL은 앞서 언급한 문제에 직면하지 않을까? 논문상에는 그냥 직관적인 방법이라고만 설명하는데, 나름대로 추론해봤다. 먼저 Representation 공간에서 생각해보자. 처음에 Target을 무작위로 초기화하므로 시각적으로 다른 이미지들은 공간상에서 거리가 멀게, 유사한 것들은 가깝게 임베딩 될 것이라고 가정할 수 있다.

여기서 기존 방법인 SimCLR은 동일한 이미지의 변형들(Positive Pairs)은 가깝게하면서 앞서 언급한 문제를 피하기 위해 다른 이미지의 변형들(Negative Pairs)과는 멀어지게 했다. 이와 달리 BYOL은 Target을 학습시키지 않고 Online의 학습을 위한 라벨을 만드는데 사용한다. 게다가 Target은 매우 느리게 변화한다. 따라서 Online이 학습되도 그 결과물들은 공간상에서 Target의 초기 위치와 크게 다르지 않을 것이고, 앞서 언급한 모든 이미지들을 하나의 Representation으로 예측하는 문제를 예방할 수 있다.

하지만, 문제는 예방 할 수 있어도 그렇게 얻은 Representation이 좋은 성능을 보일까? 저자들은 이를 증명하기위해 무작위로 초기화 시킨 두 네트워크로 위 과정을 한 번만 수행했고, 그렇게 얻은 모델로 ImageNet Linear Classification 성능을 측정했다.

여기서 Linear Classfication은 SSL에서 성능 측정을 위해 자주 사용되는 방법으로, Feature Extractor의 역할을 수행하는 선 학습된 모델은 고정시키고 뒤에 선형 분류기만 학습시켰을때의 성능을 말한다.

놀랍게도 이때 top-1 정확도가 $18.8\%$로, 무작위로 초기화한 모델의 성능인 $1.4\%$보다 월등하다. 따라서 저자들은 이 방식을 반복하면 성능이 개선될 것이라고 생각하고, BYOL을 제안한다.

BYOL이 어느정도 좋은 성능을 보장하는 근거는, SimCLR과 BYOL이 사용하는 수식을 비교에서도 확인할 수 있다.

\[\mathrm{InfoNCE}_\theta \triangleq \frac{2}{B}\sum^B_{i=1}S_\theta(v_i,v'_i)-\beta\cdot\frac{2}{B}\sum^B_{i=1}\ln\left(\sum_{j\not = i}\exp\frac{S_\theta(v_i,v_j)}{\alpha}+\sum_{j}\exp\frac{S_\theta(v_i,v'_j)}{\alpha}\right) \tag 3\]

SimCLR에서 사용하는 InfoNCE는 (3) 식에서 $\beta=1$일때로 간단히 다음과 같다. 첫번째 항은 Postive Pairs, 두번째 항은 Negative Pairs에 관한 식이다.

\[\frac{2}{B}\sum^B_{i=1}S_\theta(v_i,v'_i)-\cdot\frac{2}{B}\sum^B_{i=1}\ln\left(\sum_{j\not = i}\exp{S_\theta(v_i,v_j)}+\sum_{j}\exp{S_\theta(v_i,v'_j)}\right)\]

BYOL은 (3) 식에서 $\beta=0$일때로 다음과 같다.

\[\frac{2}{B}\sum^B_{i=1}S_\theta(v_i,v'_i)\]

Negative Pairs에 관한 식이 없고, 두 식에서 같은 표기인 $S_\theta$를 사용했지만 내부적으로 다른데, 여기서 $S_\theta$는

\[S_\theta(u_1, u_2)\triangleq\frac{\left\langle\phi(u_1),\psi(u_2)\right\rangle}{\|\phi(u_1)\|_2\cdot\|\psi(u_2)\|_2}\]

으로, 처음 소개한 그림의 모델을 기준으로 $z_\theta=g_\theta(f_\theta)$라 할 때 SimCLR의 경우는 Target Network와 Predictor가 없으므로 $\phi(u_1)=z_\theta(u_1)$, $\psi(u_2)=z_\theta(u_2)$이고, BYOL의 경우는 둘다 있으므로는 $\phi(u_1)=q_\theta(z_\theta(u_1))$, $\psi(u_2)=z_\xi(u_2)$이다. 결과적으로, 좋은 성능을 보였던 SimCLR의 변형이 BYOL이라 좋은 성능을 보인다고도 볼 수 있다.

Ablation Studies

기존 연구들은 Negative Pairs를 많이 사용해야 했기때문에 Batch size의 영향을 많이 받았고, SImCLR의 경우는 모델이 각 사진의 Color Histogram을 이용해 유용한 정보를 학습하지 않고도 예측을 할 수 있어 색상에 관한 Augmentation이 없으면 성능 하락이 심했다. 하지만 BYOL은 Negative Pairs를 사용하지 않으면서 Target의 출력을 예측하도록 Online을 학습시키므로 Color Histogram도 추가적인 정보로 이용한다. 따라서 두 요소들에 상대적으로 덜 민감하고, 실혐 결과도 다음과 같이 나타났다.

이 외에도 Target을 Online의 지수이동평균으로 사용했는데, 이때 그 정도를 결정하는 파라미터 $\tau$와 앞서 설명한 (3)식에서 $\beta$, 또 학습시 Target Network과 Predictor, Bootstrap 사용 여부의 영향도 비교했다.

왼쪽 표부터 살펴보면 Target을 아예 업데이트 하지 않는것보다 아주 적더라도 업데이트 해주는게 성능이 좋음을 알 수 있다. 저자들은 이에 관해서는 자세히 설명하진 않고, Target이 $\tau$가 0일때는 Online과 동일하고, 1보다 작을때는 Online의 좀 더 안정된 버전을 나타낸다고만 말하고 넘어갔다.

오른쪽 표를 살펴보면 Negative Pairs를 사용하지 않을때($\beta=0$) 성능이 좋은것은 BYOL뿐임을 알 수 있다. 또한 여섯번째 행의 결과인 SimCLR에서 Target Network를 사용한 결과를 보면 Target을 사용하더라도 Bootstrap과정, 즉 반복적으로 학습을 시켜주지 않으면 처참한 성능을 보임을 알 수 있다.

결론

BYOL은 대부분의 SSL 성능 평가에서 기존 방법들보다 뛰어난 성능을 보이지만, 여전히 Vision을 제외한 다른 분야에선 적절한 Augmentation을 찾이 못해 적용하기 어렵다. 하지만 각 분야에 따른 Augmentation 방법만 연구된다면 충분히 응용가능한 방법이다.

개인적으로 덧붙이면 대용량의 Batch Size를 이용하지 못하는 환경에서도 동작하면서 기존 방법보다 뛰어난 성능을 보이는게 큰 장점으로 느껴졌고, ImageNet Classification with Noisy Student의 핵심 방법인 Self-Training을 SSL에 가져온 방식으로 보였다. Noisy Studnet와 이 논문모두 기존 방법보다 뛰어난 성능을 보였는데, 그 이유를 설명할 수 있게되면 또 다른 발전이 가능하지 않을까?