RandAugment: Practical automated data augmentation with a reduced search space

관련 링크 : https://arxiv.org/abs/1909.13719

• 기존 AutoAugment 계열의 방식들의 두 개의 Search Phase(Proxy/Larger)를 하나로 줄임
• Operation 종류, 적용 확률과 적용 정도를 모두 무작위로 바꾸어서 Search Space를 줄임

Intro

데이터 도메인에 맞는 Data Augmentation(DA)을 얻기 위해서는 도메인에 관련된 전문 지식이 요구된다. 따라서, DA들도 AutoML 방식으로 디자인하는 연구들이 나타나기 시작했다. AutoAugment로 대표되는 이 방식은 NAS에서 모델을 찾는 것 처럼 데이터셋에 적합한 DA들을 찾아낸다. 하지만 이 방식은 너무 방대한 Search Space를 탐색하기 때문에 많은 연산량을 요구하므로, 적합한 DA를 찾길 원하는 데이터셋 전체를 이용해 찾지 않고, 샘플링한 작은 데이터셋에 대해서 찾고 이를 전체에 적용한다.

결과적으로, Search Phase가 이 후 Proxy Task라 칭할 작은 데이터셋에서 적합한 DA를 찾는 과정과, Larger Task라 칭할 전체 데이터셋에서 DA의 성능을 확인하는 과정으로 나뉘게 된다. 이런 과정이 만들어진 이유는 연산량 때문이지만, 이렇게 만들어진 과정이 받아들여 지는 이유는 Proxy Task에서의 결과가 Larget Task의 성능을 대변할 만한 근거라는 가정 때문이다.

오늘 소개할 논문에서 저자들은 바로 위의 가정에 의문을 품는다. 아무리 생각해봐도 학습 과정에 가장 적절한 DA이 모델과 데이터셋의 크기에 무관하다는 것은 말이 안되기 때문이다. 1000장의 데이터셋에서 가장 좋은 성능을 내는 DA이 50000장의 데이터셋에서 가장 좋은 성능을 내는 DA와 같을 수 있을까? 작은 크기의 모델에서 가장 좋은 성능을 내는 DA가 큰 모델에서도 가장 좋을까? 두 질문에 대한 정확한 답은 수 많은 실험으로 연역적으로만 알 수 있겠지만, 경험적으로 답은 아니라고 느껴진다.

따라서, 저자들은 Proxy Task가 Sub-optimal하다고 보고 이를 제거하고 이전 연구들의 실험들을 근거삼아 Search Space를 극도로 줄인다. Search Space가 이전 연구들에 비해 엄청나게 줄어서 Search Algorithm으로는 간단한 Grid Search를 사용한다.

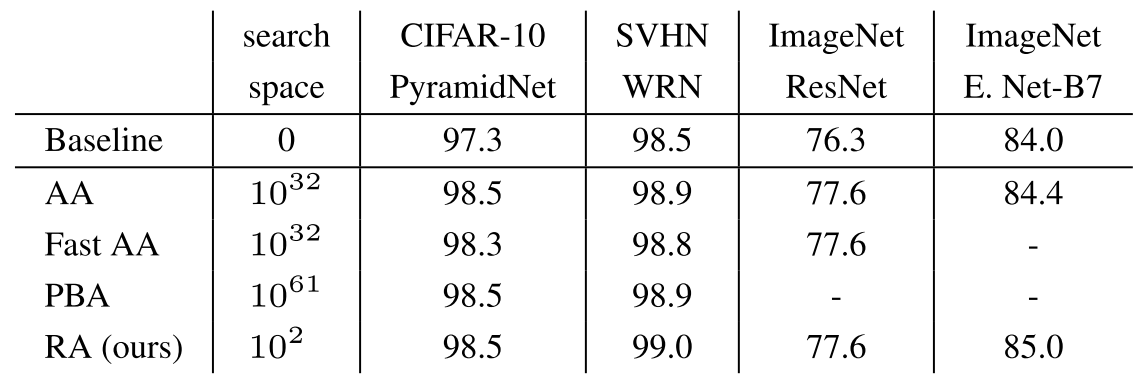
RandAugment

About Magnitude

Proxy Task가 Sub-optimal함을 보이는 실험을 하기 전에, 이 실험의 배경이 되는 Search Space에 대한 이야기를 먼저 해보자.

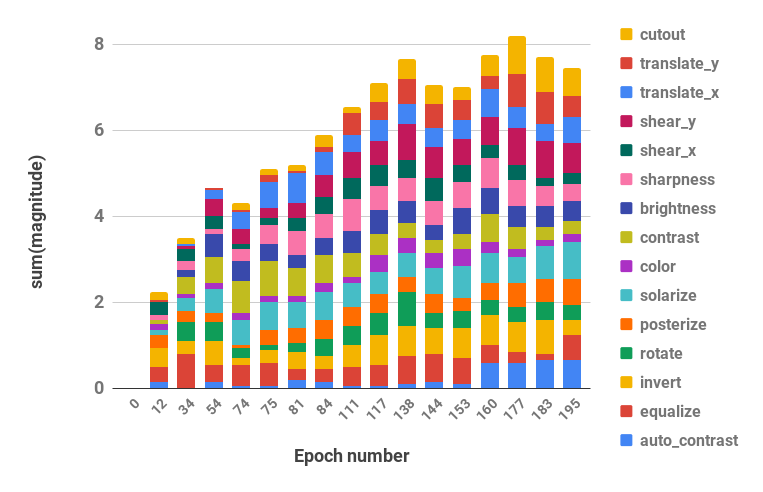
이전 연구인 AutoAugment에서 Operation의 적용 정도인 Magnitude(Mag)와 적용 확률 Probability(Prob)를 모두 무작위로 주었을 때 성능이 낮아졌고, 낮아진 수치가 Operation까지 무작위로 주었을 때와 거의 차이가 없다는 점을 발견했다. 이는 Mag와 Prob가 중요한 역할을 함을 보여주었다. 그 다음 연구에서 Operation의 적용 정도인 Magnitude가 학습이 진행될 수록 커지는 경향이 있음을 발견했다. Epoch에 대한 Mag의 그래프인 위 그림을 보면 학습이 진행 될 수록 Mag의 총합이 커진다.

저자들은 이를 Mag에 대한 적절한 Scheduling만 있으면 모든 Operation에 대해 Mag를 구할 필요가 없지 않을까 하는 가능성으로 보았다. 그래서 예비실험으로 두 값 사이에서 무작위로 뽑기, 값 하나로 고정, 선형적으로 증가, Upper Bound를 증가시키는 무작위 뽑기 중에서 비교했고, 네 가지 경우가 거의 차이가 없어 최종적으로 하나의 고정값을 따르는 것으로 Search Space를 줄였다.

About Operation and Probability

또, 저자들은 모든 Operation에 동일한 Mag를 주는 것 외에도 Operation의 종류와 Prob도 건드렸다. 이전 연구들은 Operation의 종류와 Prob를 모두 찾았는데, 저자들은 **$K$개의 Operation들이 있을 때 모든 Operation에 $\frac{1}{K}$의 확률을 부여하고 찾을 DA에 몇 개의 Operation을 적용할지 정하는 파라미터 $N$을 두어 생성될 이미지의 종류를 $K^N$로 다양하게 하면서 Search Space를 줄였다. **즉, 이전에는 Operation의 개수 $K$와 각 Operation의 Prob(이산적으로 $P$ 단계)를 구해야 했으므로 한 Operation을 위해 $K\times P$의 Search Space를 뒤져야 했지만, 저자들은 이를 $N$의 Search Space만 뒤지도록 했다.

AutoAug는 $N=2$(Subpolicy의 Operation 수)로 고정하고 $K\times P$를 뒤진 반면 RandAug는 $K\times P$를 놔두고 $N$을 찾는 방식이다.

그런데 이렇게 했을 경우 성능에 영향이 없을까? 먼저 Operation을 무작위로 택한다는 사실에 주목해 보자. 사실 데이터셋에 따라 효과적인 DA들이 다르다는건 당연하다. SVHN 같은 숫자 위주의 데이터셋은 당연히 기하학적 변형이 효과적일테고, CIFAR은 그것들 보다는 색 변형이 효과적이다. 그렇기 때문에 AutoAugment도 효과적인 Policy를 찾기 위해 적절한 Operation들도 찾았다. 저자들도 이를 의식했는지 RandAugment의 Operation들의 개수에 따른 성능 비교를 수행했다.

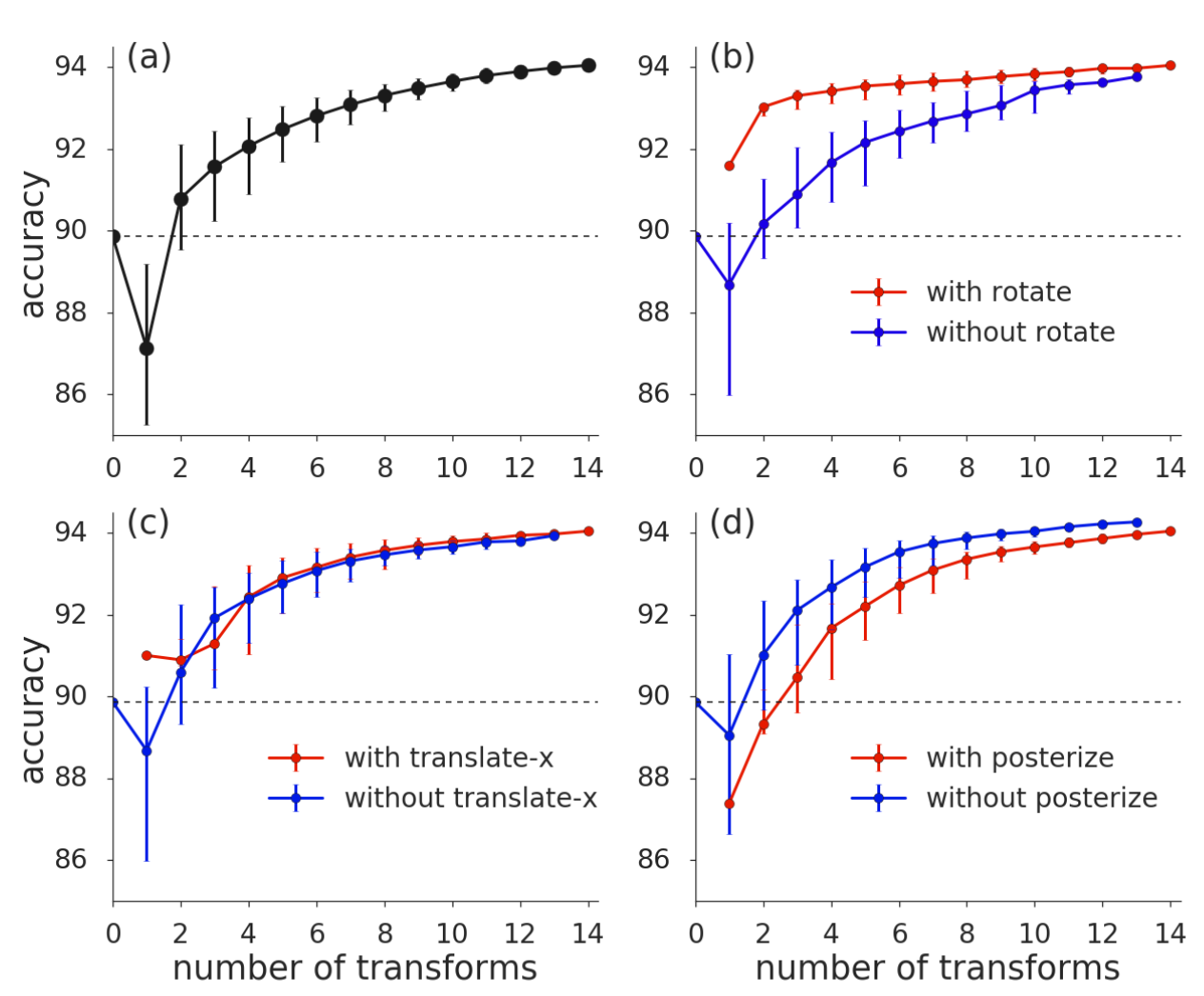
CIFAR 10에서 $N=3, M=4$로 실험을 진행했다. 점선은 No Augmentation의 성능이다

앞선 연구들처럼 효과적인 DA도 존재하고 효과가 떨어지는 DA도 존재함이 확인된다. 하지만 Operation의 개수가 많아지면 거의 비슷한 성능을 내는 것을 볼 수 있다. 따라서 Search Space를 줄이는 것에 비해 성능 손실이 미미하므로 효과적인 디자인이다.

다음으로는 Prob가 Uniform하다는 점을 주목해 보자. 앞서 이전 연구에서 Mag와 Prob가 성능에 영향을 주는 요소임을 밝혔다. 따라서 모든 Operation들을 어떻게 뽑을지도 상당히 중요할 것이다. 저자들은 이와 관련된 실험으로 몇 몇 미분가능한 DA들에는 학습 가능한 적용 확률을 추가해 학습시켰다.

이때 사용된 방법은 Fast AutoAugment에서 사용한 Density Matching이라고 하는데, 자세한건 논문을 참조

결과를 보면 RandAug보다 좋지만 많이 높진 않다. 이 방식은 이미지 크기가 커지면 계산량이 너무 많아져서 실 적용은 쉽지 않다고 하므로, RandAug처럼 Uniform하게 추출하는게 효과적으로 보인다.

Methods

결과적으로 AutoAugment에서 $3\times 10^{32}$에 육박하던 Search Space가 $10^2$까지 줄이면서, 기존 SOTA와 비견할 만한 성능을 보인다. 또 구현도 간단 해진다.

transforms = [
  'Identity', 'AutoContrast', 'Equalize', 'Rotate', 'Solarize', 'Color', 'Posterize', 
  'Contrast', 'Brightness', 'Sharpness', 'ShearX', 'ShearY', 'TranslateX', 'TranslateY'
]
def randaugment(N, M): 
  """
  Generate a set of distortions.
  Args: 
    N: Number of augmentation transformations to apply sequentially.
    M: Magnitude for all the transformations. 
  """
  sampled_ops = np.random.choice(transforms, N) 
  return [(op, M) for op in sampled_ops]

Separate Proxy Task is Sub-optimal

RandAug의 Search Space에 대해 충분히 이야기 했으니, 앞선 연구들의 Proxy Task에 Optimal한 DA들이 Larger Task에서는 Sub-optimal함을 보이자. 이는 매우 간단하다. RandAugment가 Search Space를 극단적으로 줄이긴 했으나, 결과 Policy의 다양성은 비슷하기 때문에, 여러 모델과 데이터셋 크기에 대해 찾아야 하는 파라미터 Mag가 달라진다면 Proxy Task의 DA가 Sub-optimal함이 증명된다.

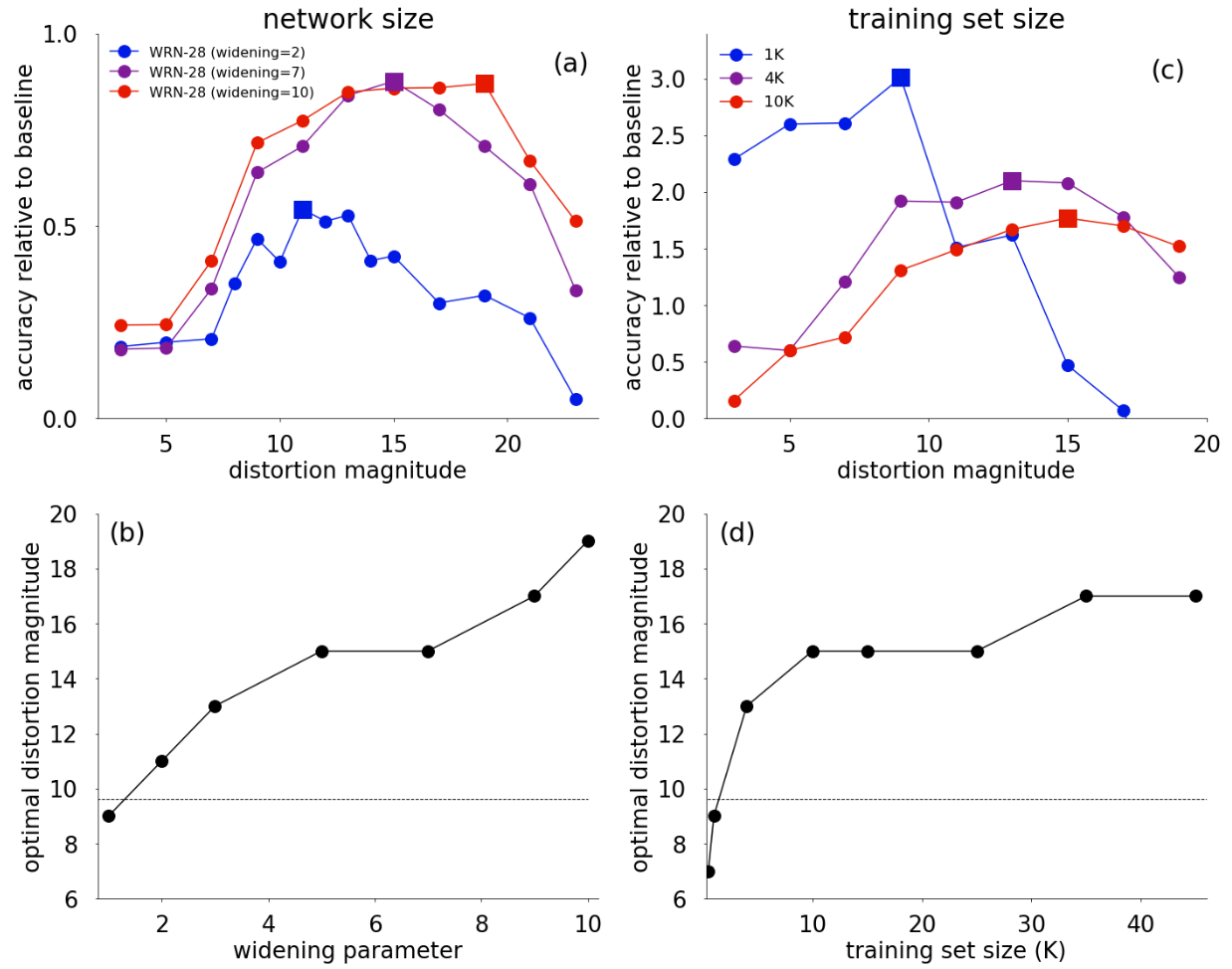
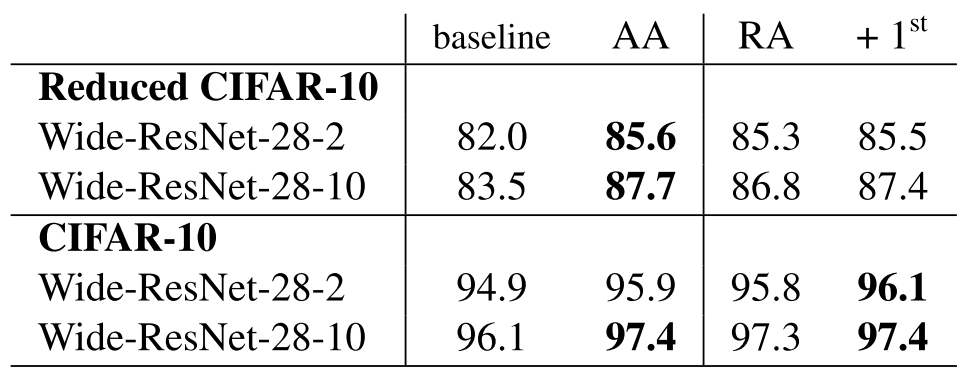
첫 번째 행에서는 모델의 크기와 데이터셋의 크기에 따라 Optimal Mag가 다름을 보여준다. DA가 하나의 규제이고 Mag가 규제의 정도라고 생각해 보면 (a)는 Variance가 큰 모델에 강한 규제, 작은 모델에 약한 규제가 걸어줘야 함을 생각했을때 합당해 보인다. (b)는 의아할 수 있는데, 데이터셋이 작을수록 강한 Mag로 Aug를 강하게 해야 할 것 같지만 오히려 약한 Mag가 Optimal함을 보여준다. 저자들은 이를 작은 데이터셋에 강한 Mag는 낮은 신호대잡음비를 이끌 수 있기 때문이라고 추측한다.

두 번째 행의 결과들은 Proxy Task에서 찾은 Optimal Mag와 Larger Task에서 찾은 Optimal Mag가 다름을 보여준다. 즉, Proxy Task의 Optimal DA가 Sub-optimal 하다는 결정적 증거이다.

Remarks

최근 관심있게 본 논문들이 모델에 추가적인 규제를 넣는 의미로 RandAugment를 많이 사용해서 보게된 논문이다. 바로 보니 와닿지가 않아서 AutoAugment부터 보게 됬는데, NAS 관련 논문을 재밌게 읽어서 그런지 흥미로운 내용이 많은 것 같다. 제안한 방법은 간단한데 방법을 도출하게 된 근거들이 인상깊은 연구인듯.