Swin Transformer: Hierarchical Vision Transformer using Shifted Windows

관련 링크 : https://arxiv.org/abs/2103.14030

• 층이 깊어 질수록 Patch Merging을 통해 패치 수를 줄임
• Shifted Window를 이용해 효율적인 연산을 하면서도 성능 향상을 이뤄냄
• Absolute Positional Embedding대신 Relative Position Bias를 이용

Intro

Transformer는 자연어 처리 분야에서 사용되어 좋은 성능을 보인 후, Vision분야에 적용되었다. 초기에는 자연어에서 문장의 단어를 토큰으로 이용했던 것처럼 이미지의 픽셀을 토큰으로 이용해 Transformer를 이용했다. 하지만 픽셀들간의 Self-Attention이 많은 연산량을 요구했고, 이미지의 픽셀은 문장의 단어만큼 의미있는 정보를 가지고 있지 않아 좋은 성능을 낼 수 없었다.

이를 해결하기 위해 이미지를 패치단위로 잘라 패치를 하나의 토큰으로 보는 방법(ViT)이 제시되었는데, 픽셀단위에서 패치단위로 바뀌면서 토큰의 수가 줄어 연산량이 감소했고, 픽셀에 비해 패치는 의미있는 정보를 가졌다. 결과적으로 이는 SOTA를 달성했고, Transformer가 본격적으로 Vision분야에 적용되는 계기가 되었다.

하지만, Transformer 계열의 모델들은 여전히 CNN처럼 General Purpose Backbone으로 쓰이기에는 많은 한계점들을 가지고 있었다. 기존 모델들은 모든 레이어에서토큰의 수와 차원이 고정되어 있는데, 자연어의 단어와 달리 영상의 이미지는 요소들의 크기가 다양하므로 Vision에 적합하지 않다. 또 Semantic Segmentation이나 Object Detection에서는 각 픽셀들에 대해 예측해야하므로 고해상도 이미지를 다루는데, Transformer 계열은 이미지 크기의 제곱에 비례하여 연산량이 증가하므로 여전히 너무 많은 연산량을 요구했다.

왜 Transformer의 연산량은 이미지 크기의 제곱에 비례하는가?

\[O(\text{Self-Attention})=4hwC^2+2(hw)^2C\\ \text{※ SoftMax는 복잡도 계산에서 제외, Multi-Head도 다르지 않음}\]

• 이전 토큰의 차원을 $C$, $\text{query, key, value}$의 차원도 $C$
• $hw$는 토큰의 개수($h=\frac{\text{Image Height Size}}{\text{Patch Height Size}}$, $w=\frac{\text{Image Width Size}}{\text{Patch Width Size}}$)
• 첫 번째 항 → $3hwC^2$: 이전 토큰을 $\text{q, k, v}$로 임베딩 + $hwC^2$: Attention 이 후 결과를 Linear = $4hwC^2$
• 두 번째 항 → $(hw)^2C$: $\text{q}\cdot \text{k}^T$ + $(hw)^2C$: $\text{attn}\cdot \text{v}$

따라서 저자들은, 위의 문제들을 해결할 수 있는 새로운 형태의 Swin Transformer를 제시한다.

Swin Transformer

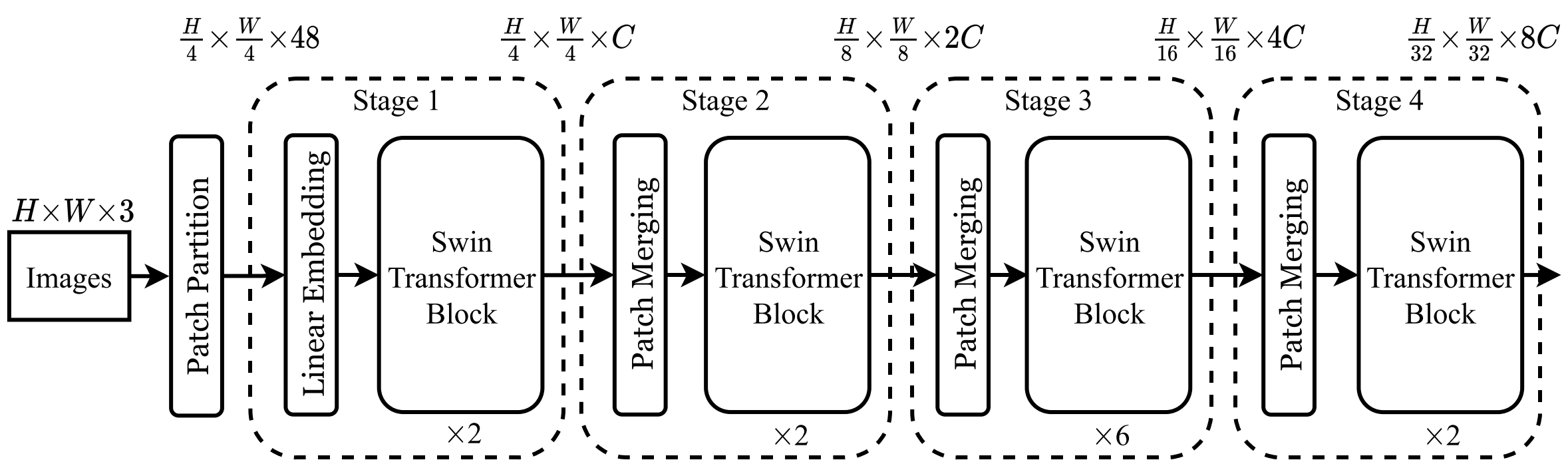
저자들이 문제라고 지적한 점은 두 가지로, 1. 토큰들의 크기가 고정되어 Vision과 어울리지 않는다는 점과 2. 연산량이 이미지 크기의 제곱에 비례한다는 점이다. 저자들은 각 문제를 Patch Merging과 W-MSA/SW-MSA로 해결했다.

Patch Merging

위의 전체 구조를 보면, Stage가 진행됨에 따라 토큰들의 개수는 $1/4$씩 줄어들고, 토큰의 차원은 2배 늘어나는 것을 알 수 있다. 이는 위 구조의 Patch Merging 부분으로 $2\times 2$의 이웃 토큰들을 합친 후 $4C\times2C$의 파라미터를 가진 Linear Layer로 이루어진다. 이를 통해 레이어가 깊어질수록 CNN처럼 Spatial Resolution(Transformer의 토큰의 수)는 감소하고, 피처맵의 차원 수(토큰의 차원 수)는 증가하는 구조를 가지게 된다.

논문에서 이 부분을 제안은 했는데 성능에 기여한 바를 크게 다루지 않았다.

W-MSA/SW-MSA

Intro에서 설명 했 듯, 기존 Transformer 모델들은 이미지 크기의 제곱에 비례하는 복잡도를 가졌다. 저자들은 이를 Window based Self-Attention(W-MSA)와 Shifted Window based Self-Attention(SW-MSA)로 해결한다. W-MSA는 모든 패치에 대해 Global Attention을 하지 않고, 고정된 크기의 서로 중복되지 않은 Window를 지정한 후, Window안의 토큰들끼리만 Attention하는 방식이다. 이를 이용하면 Self-Attention이 이미지 크기에 선형적으로 비례한다.

왜 Swin-Transformer의 연산량은 이미지 크기에 선형적인가?

\[O(\text{W-MSA})=4hwC^2 + 2M^2hwC \\ \text{※ 앞선 } O(\text{Self-Attention}) \text{과 동일 조건}\]

• 첫 번째 항은 Intro의 $O(\text{Self-Attention})$과 동일하고, $M$은 Window Size를 뜻한다.
• 두 번째 항에서는 $q_{M^2}, k_{M^2}, v_{M^2} \in \mathbb R^{M^2\times C}$이고, 이 연산을 $\frac{hw}{M^2}$만큼 하므로
  • $M^2hwC$: $q_{M^2} \cdot k_{M^2}^T \times \frac {hw}{M^2}$ + $M^2hwC$: $\text{attn} \cdot v_{M^2} \times \frac{hw}{M^2}$

그러나 이 방식을 이용하면 Window간에는 Attention이 이루어지지 않고, Patch Merging이 이용된다 하더라도 양 끝단에 존재하는 토큰들은 Attention 할 수 없다. 따라서, 고정된 Window($M\times M$)를 크기의 반($\frac{M}{2}$)만큼 이동시키고 Attention을 수행한다. 따라서, Swin Transformer Block은 W-MSA와 SW-MSA가 번갈아 사용되고, 이때 그 과정과 모델 구조는 아래와 같다.

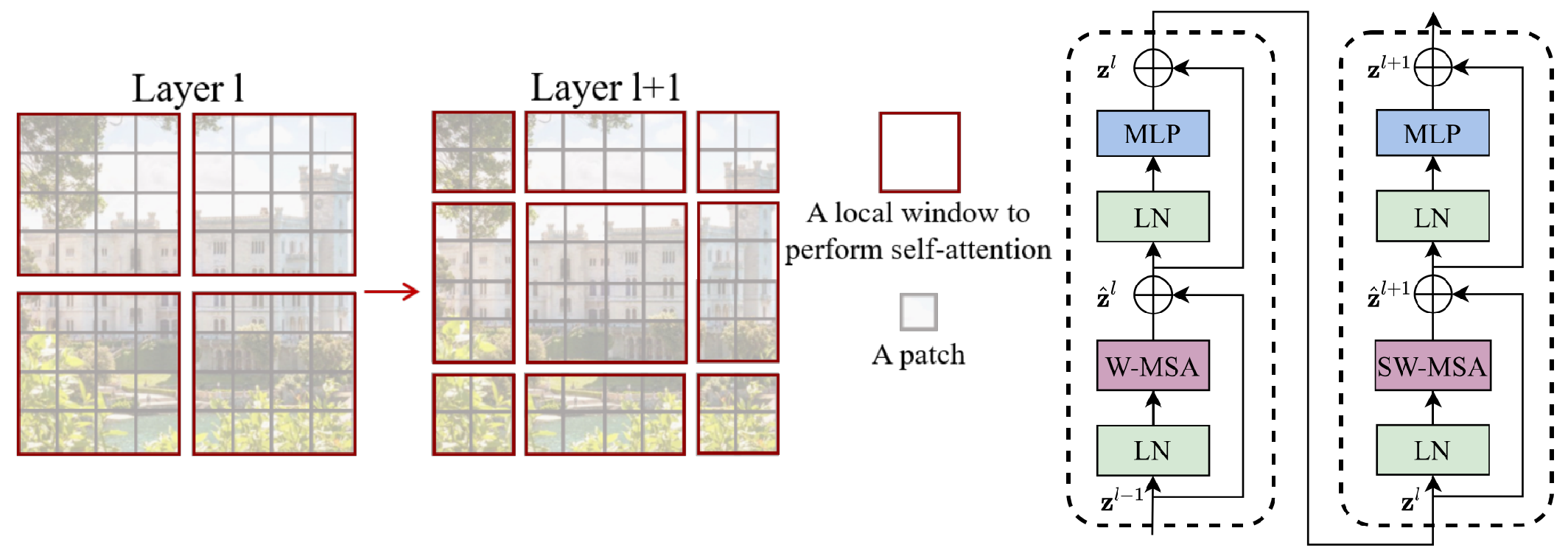
그런데, 위 그림의 Layer 1+1을 보면 의아한 점이 있다. 바로, Layer 1보다 작은 Window들이 생긴다는 점이다. 구현상 편의를 위해서는 고정된 크기의 Window에 대해 Attention을 하는게 좋으므로, Shift 후에 Zero padding을 한 후, $\text{attn}\cdot \text{v}$ 연산에서 $\text {attn}$을 Mask해야 한다. 하지만 이 경우 Window의 개수가 많아지고, 결국 Mask해서 이용하므로 쓸데없는 연산이 발생한다. 따라서 저자들은 Window 개수를 늘리지 않고 위 Shift를 수행하기 위해 Cyclic Shift를 제안한다.

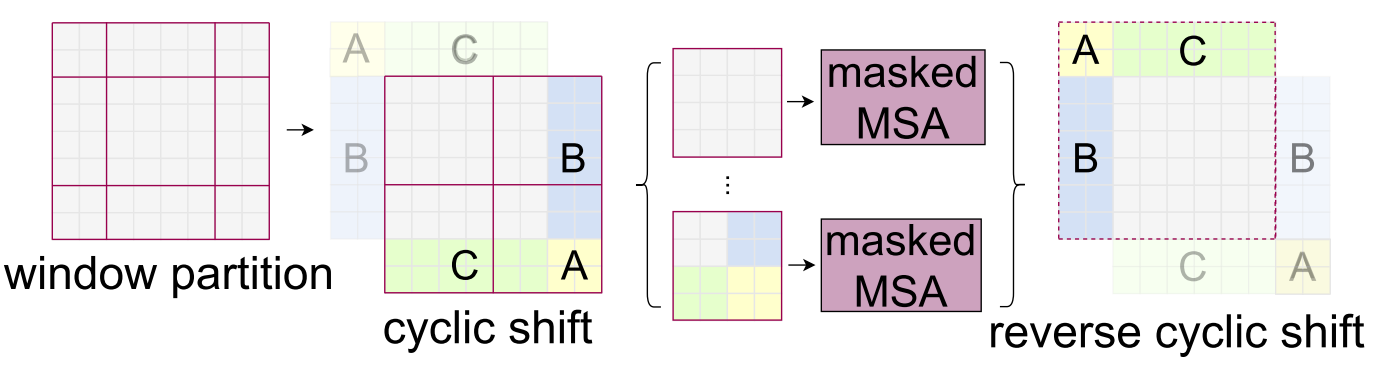
Cyclic Shift는 위 그림과 같이 단순히 A, B, C를 반대쪽에 붙여서 Window 개수를 늘리지 않는 방법이다. 이때, 새로 붙인 부분들은 서로 인접해 있지 않으므로 원래 구역들끼리 독립적으로 Attention 하도록 Masked 해준다. 아래 코드는 $\text{SoftMax}$전에 $\text{attn}$에 더해질 Mask를 만드는 코드다. create_mask를 이용해 만든 mask는 $\text{SoftMax}$전에 $\text{attn}$에 더해지고, 각 구역은 독립적으로 Attention이 수행된다.

def create_mask(window_size, displacement, upper_lower, left_right):
    mask = torch.zeros(window_size ** 2, window_size ** 2)
    if upper_lower: #위 그림의 C+A 구역
        mask[-displacement * window_size:, :-displacement * window_size] = float('-inf')
        mask[:-displacement * window_size, -displacement * window_size:] = float('-inf')
    if left_right: #위 그림의 B+A 구역
        mask = rearrange(mask, '(h1 w1) (h2 w2) -> h1 w1 h2 w2', h1=window_size, h2=window_size)
        mask[:, -displacement:, :, :-displacement] = float('-inf')
        mask[:, :-displacement, :, -displacement:] = float('-inf')
        mask = rearrange(mask, 'h1 w1 h2 w2 -> (h1 w1) (h2 w2)')
    return mask

결과적으로 약간의 Overhead로 MSA의 복잡도를 이미지 크기에 선형적으로 감소시킬 수 있다.

Relative Position Bias

추가적으로, 저자들은 성능을 올리기 위한 방법도 제안했다. 단순히 기존 ViT가 $\text{q, k, v}$를 임베딩하기 전에 Positional Encoding을 해 주었다면 저자들은 각 $\text{q}$의 위치를 기준으로 $\text{k}$의 상대적인 위치를 이용해 $\text{attn}$에 임베딩을 더해준다.

\[\text{Attention}(Q, K, V)=\text{SoftMax}(\frac{QK^T}{\sqrt d}+B)V\]

Swin Transformer는 $M\times M$의 Window를 이용하고 Bias이므로, $\hat B\in \mathbb R^{2M-1\times 2M-1}$에서 Width, Height 축의 상대적인 위치를 이용해 인덱싱해 $B\in \mathbb R^{M^2 \times M^2}$를 만들어 이용한다.

def get_relative_distances(window_size): #Window 크기에 따른 query 기준 key의 상대적인 거리 얻기
    indices = torch.tensor(np.array([[x, y] for x in range(window_size) for y in range(window_size)]))
    distances = indices[None, :, :] - indices[:, None, :]
    return distances #distances.shape = (window_size**2, window_size**2, 2)
... 생략
relative_indices = get_relative_distances(window_size) + window_size - 1 
pos_embedding = nn.Parameter(torch.randn(2 * window_size - 1, 2 * window_size - 1))
... 생략
attn += pos_embedding[relative_indices[:, :, 0], relative_indices[:, :, 1]]

Results

위 방법들을 이용해 의미있는 성능 향상을 이뤄냈다.

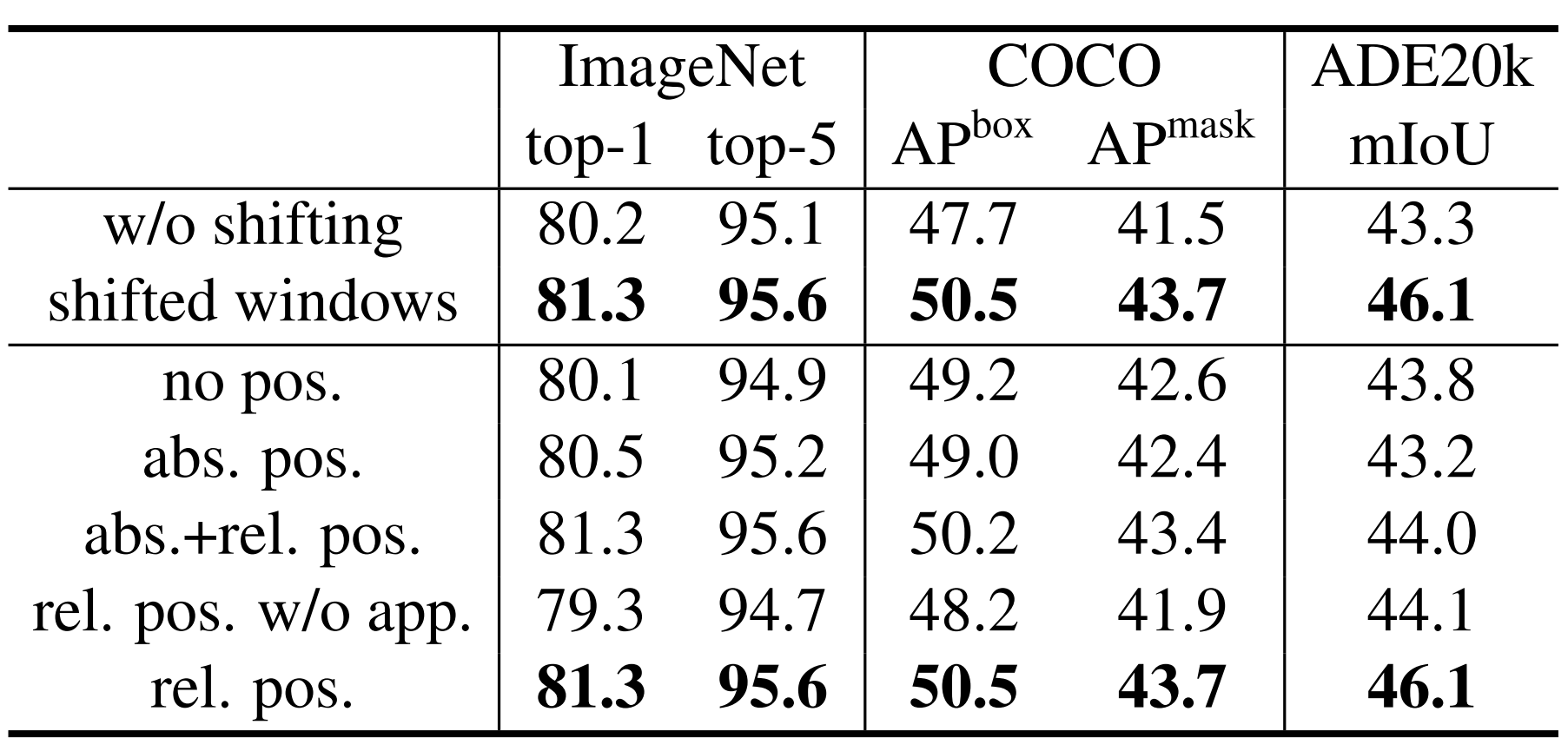
• $\text{abs}$는 ViT의 Absolute Positional Emcoding

• $\text{rel}$은 저자들이 제안한 방식

• $\text{app}$은 첫 번째 Scale Dot Product항을 의미

  $\text{app}$은 $\text{Attention}(Q, K, V)=\text{SoftMax}(\frac{QK^T}{\sqrt d})V+B$를 의미하는 것으로 추정 됨

그리고 이전 SOTA 및 비슷한 성능의 모델들과 다양한 실험을 수행했는데, 몇몇 분야에서는 SOTA를 달성했고 속도 대비 성능을 비교해보면 훨씬 우월하다.

Remarks

사실 Patch Merging을 통한 Inductive Bias에 관심이 있어서 보게 된 논문인데, 이 부분은 거의 다루지 않고 Shifted Window에 중점을 두어서 아쉬웠다. 그리고 제시한 방법과 그 방법을 제안하게된 동기의 개연성이 잘 이해되지 않아서 이 후 새 버전이 나오면 다시 봐야 할 듯