관련 링크 : https://arxiv.org/abs/1610.02242
- Semi-Supervised Learning의 방법 중 하나인 Consistency Training의 시초격인 논문
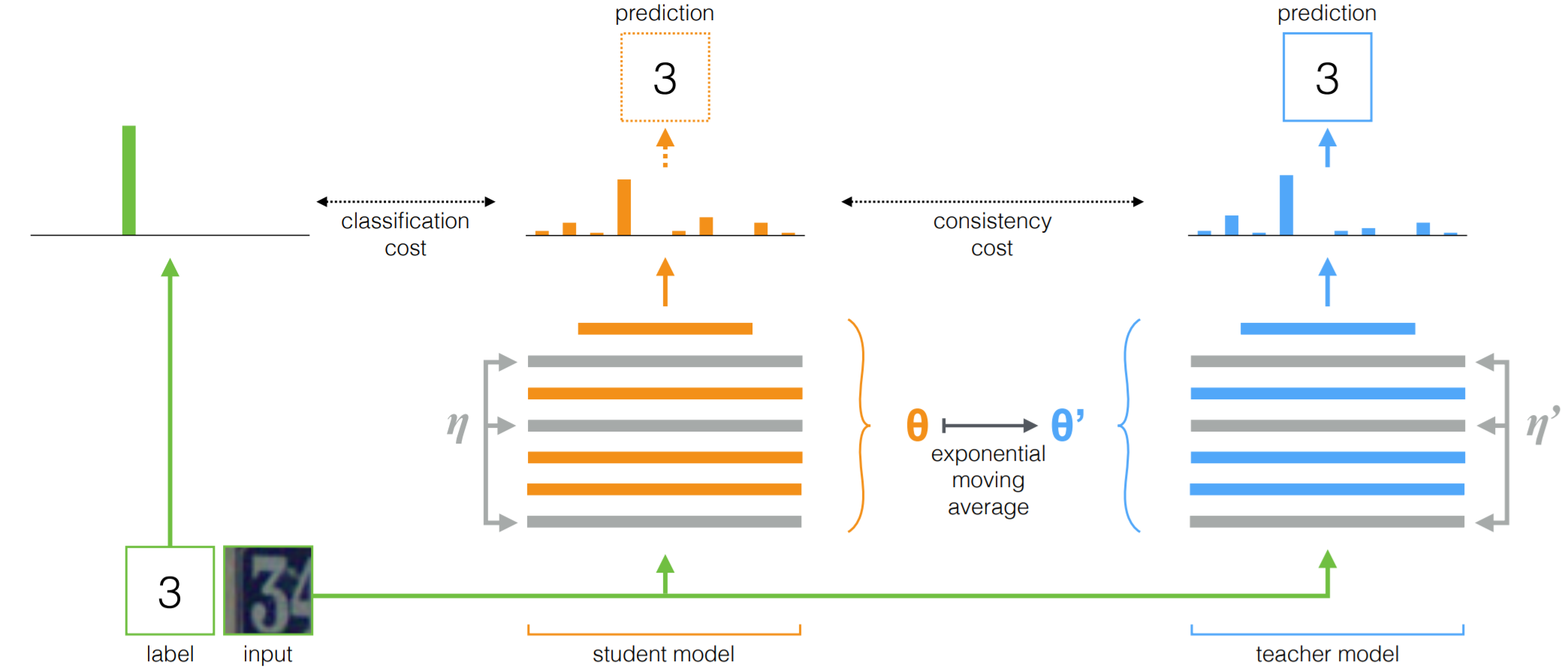
Consistency Training이란 SSL의 하부 분야 중 하나로, 입력 데이터/피처맵/은닉층에 약간의 노이즈(Gaussian/dropout/adversarial)를 추가했을때 모델의 예측이 바뀌지 않도록 모델을 규제하며 학습시키는 방법이다.
- $\boldsymbol\Pi$-model과 Temporal Ensembling이란 두가지 방법을 제안
- 당시 SOTA를 기록했고, Supervised Learning에 적용해도 효과적
Method
$\boldsymbol\Pi$-model

- $y_i$는 라벨이 있는 데이터에만 존재한다. 따라서, 라벨이 있는 데이터에서만 Supervised Loss가 계산될 수 있다.
- Stochastic Augmentation과 Dropout을 이용해 동일한 입력 $x_i$에서 다른 출력 $z_i$와 $\overset {\thicksim}{z_i}$이 나타난다.
- Supervised Loss는 cross-entropy, Unsupervised Loss는 squared difference로 계산한다. Squared difference 대신 cross-entropy를 사용해도 되는데, 전자가 더 성능이 좋았다고 한다.
- $w(t)$는 가중합시 Unsupervised Loss의 가중치를 결정하는 함수로, 80에폭 동안은 0에서 시작해 Gaussian 곡선을 따라 점점 상승시킨다. 즉, 학습 초반에는 Supervised Loss가 학습은 관장한다.
Temporal Ensembling

-
$\boldsymbol\Pi$-model은 Unsupervised Loss 계산을 위해 두 번의 추론을 요구한다. Temporal ensembling은 이를 위한 타겟 벡터 $\overset {\thicksim}{z_i}$를 이전 에폭들의 출력을 이용해 계산하므로 한 번의 추론만 요구한다.
-
네트워크의 출력을 $z_i$라 하면, 다음 에폭의 Loss 계산을 위한 앙상블 벡터 $\overset {\thicksim}{Z_i}$는 $\overset{\thicksim}{Z_i} \leftarrow \alpha \overset{\thicksim}{Z_i} +(1-\alpha)z_i$이다. 실험에서는 $\alpha=0.6$을 이용해 최근 에폭들의 출력이 더욱 반영되도록 설계했다.
-
$\overset {\thicksim}{Z_i}$를 그대로 사용하지 않고, bias correction을 위해 $(1-\alpha^t)$로 나누어 $\overset{\thicksim}{z_i}$를 구한 후 이를 이용해 Unsupervised Loss를 계산한다.
논문에서는 bias correction이 무엇인지 자세히 다루지 않으므로, 자세한 설명을 원하면 관련 논문의 bias correction 부분을 살펴보길 바람
-
-
$\overset{\thicksim}{z_i}$가 여러 에폭들의 앙상블로 계산되므로, $\Pi$-model에 비해 $\boldsymbol{\overset{\thicksim}{z_i}}$의 노이즈가 적다. 하지만 하이퍼파라미터 $\alpha$와, 이전 출력들을 저장하기 위한 $\overset {\thicksim}{Z_i}$가 추가적으로 요구된다.
Experiments
-
당시 SOTA였으므로, 기존 연구들과의 성능 비교는 적지 않았다.
-
성능비교에서 한가지 흥미로운 점은, 라벨링 된 데이터만 사용한 완전한 Supervised Learning에서도 논문의 방식이 더 좋았다는 점이다. 저자들은 논문의 방식이 Consistency를 증가시켜 모호한 예제들을 잘 구분하게 만든다고 설명한다.
이 부분이 이후 Semi-Supervised Learning의 Consistency Training 용어의 시작점이 된 것으로 추정된다.
-
Many Random Unlabeled Data .Vs Small Restricted Unlabeled Data

- 위 실험은 CIFAR-100을 라벨링된 데이터로, Tiny Image를 라벨링 되지 않은 데이터로 사용했을때 비교 실험이다. Random 500k는 무작위로 뽑은 것이고, Restricted 237k는 CIFAR-100과 라벨이 동일한 이미지들에서 뽑은 것이다.
- Restricted 237K가 Random 500k보다 성능이 좋지 않다.
- 라벨링 되지 않은 데이터로 학습시킬때, 라벨링 된 데이터와의 차이가 너무 크지만 않으면 충분하다.
Tolerance to Incorrect Labels
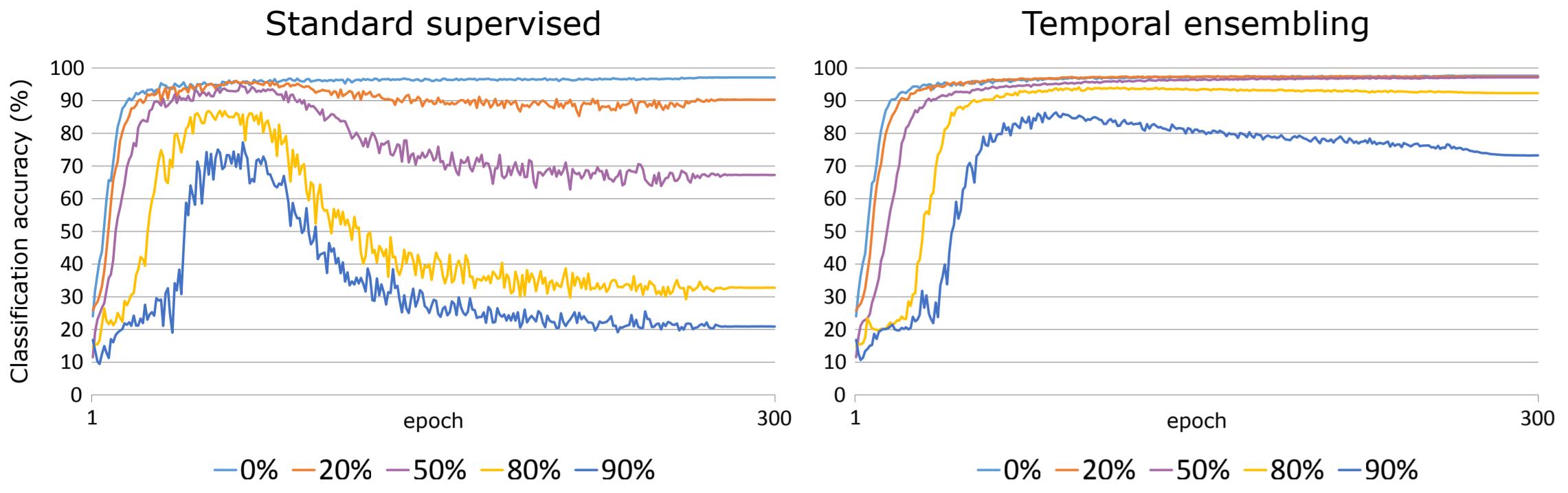
-
위 실험은 SVHN의 라벨을 특정 비율로 무작위로 바꿨을때 에폭에 따른 모델의 성능을 보여준다.
-
Temporal ensembling은 무려 80%의 라벨이 무작위로 정해졌을때도 높은 성능을 보여준다.
-
저자들은 Supervised Loss가 입력 데이터 근방을 특정 값으로 맵핑하고, Unsupervised Loss는 입력 데이터 근방을 평평하게 만들어주어 Supervised Loss가 입력 데이터를 잘못 매핑하더라도 Unsupervised Loss가 이를 고쳐주기 때문이라고 말한다.
A의 라벨이 1인데, 3으로 바꾸어서 모델에게 주었다고 가정해보자. Supervised Loss는 A를 3이 되도록 맵핑함수를 만들어 낼 것이다. 하지만 A와 비슷한 여러 데이터들이 1로 맵핑되어 있을 것이므로, Unsupervised Loss에 의해 최종적으로 A는 1에 맵핑된다.
-


Leave a comment