관련 링크 : https://arxiv.org/abs/2103.06877
Introduction
-
손수 만들던 NAS를 통해 만들던 새로운 모델을 개발하기 위해 성능과 속도의 관점에서 다양한 모델을 학습한 후 가장 좋은 모델을 학습시키는 과정이 필수적이다.
-
GPU와 TPU등의 발전으로 다양한 작은 모델들을 학습하고 그 중 하나를 선택하는 방식이 Low-compute Regimes에서 실현 가능해졌다.
-
위 과정보다 더 많은 연산을 요구하는 Intermediate-compute Regimes에 존재하는 Task들은 효과적인 Search 방법과 Search Space Design들을 통해 해결 가능하다.
Search Space Design: RegNet을 의미
-
하지만, 위의 과정을 수행할 수 없는 거대한 모델들을 찾아야 하는 High-compute Regime이 존재한다.
-
High-compute Regime에서 모델을 찾을 때, 낮은 복잡도를 가진 모델을 Depth나 Width같은 특정 차원을 단계적으로 늘려서 키우는 Network Scaling이 필수적이다.
-
EfficientNet에서 Scaling이 효과적임이 증명되었다.
-
현존하는 Scaling들은 모두 Flops 대비 성능에 초점이 맞춰져 있다.
-
동일한 Flop에 동일한 성능을 가진 모델을 만드는 다양한 Scaling 방식이 존재한다.
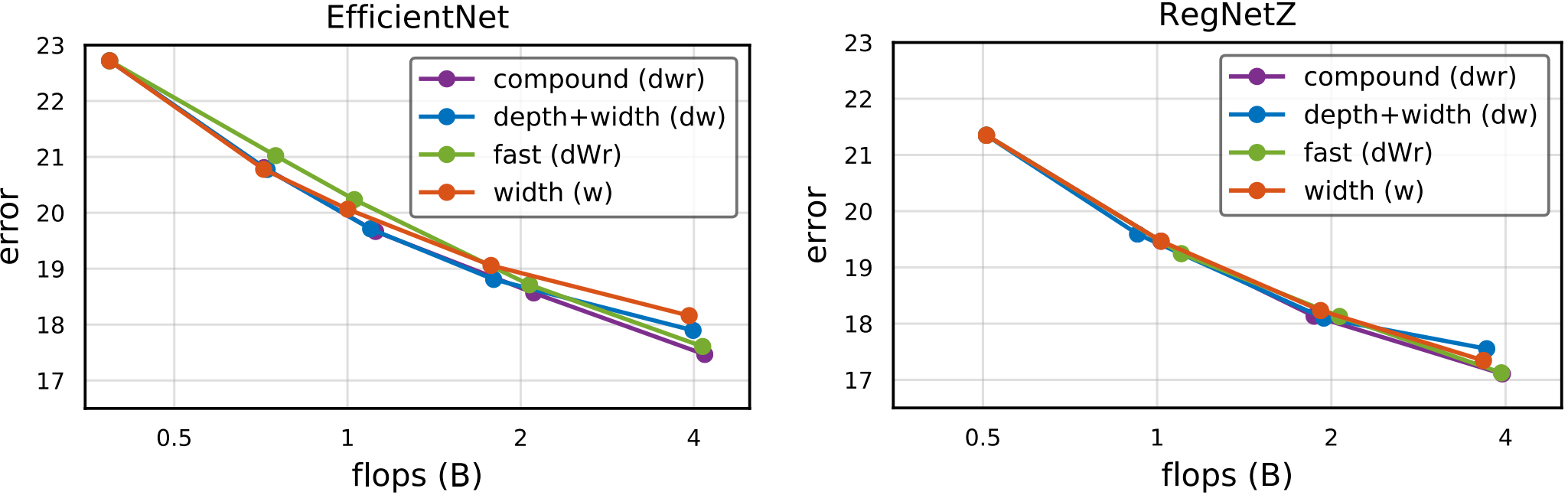
-
하지만 각 Scaling 방식은 Runtime이 다르다.
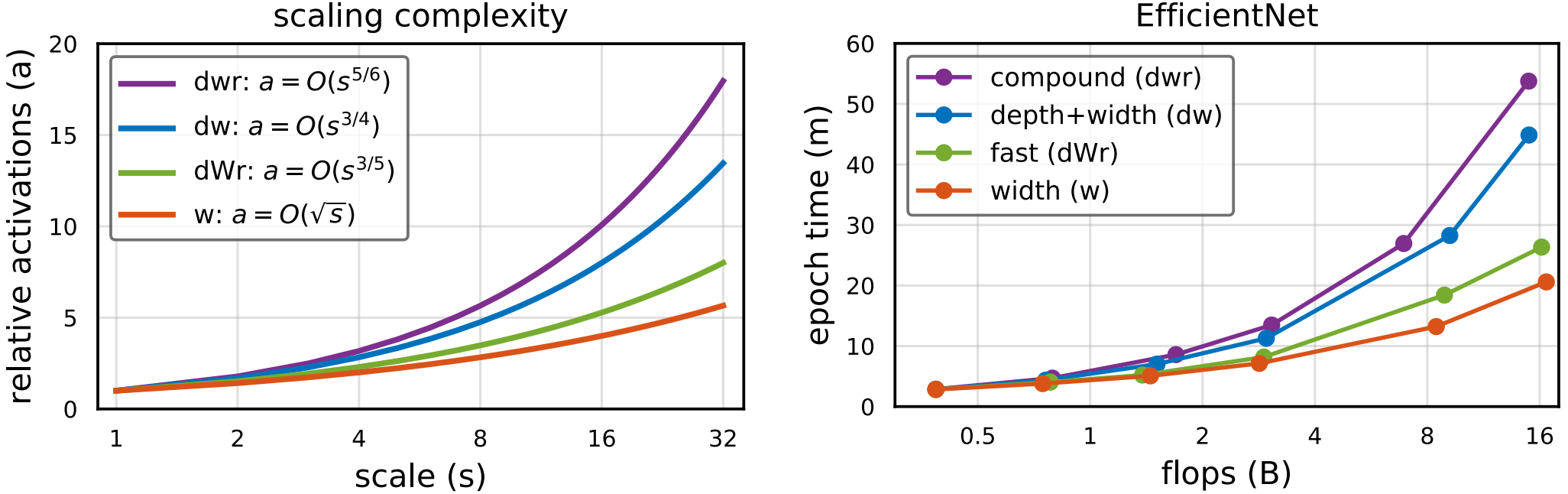
a는 depth, width, resolution을 s로 Scaling 했을 때 발생하는 Activation의 수를 나타낸다.
-
-
-
그래서, 연구에서는 Flops, Parameters, Activations를 모두 고려한 다양한 Scaling의 시간 복잡도를 분석하는 도구를 개발했다.
Complexity of Scaled Models
Complexity Metrics
- Scaling과 가장 관련 있는 특성들을 Flops($f$), Parameters($p$), Actiations($a$)이다.
- Flops: 덧셈과 곱셈의 수로 실제 Runtime을 반영함
- Parameters: 학습 되는 파라미터의 수로 Input Resolution을 반영하지 못해 실제 Runtime을 반영하지 못함
- Activations: Conv 층의 출력 Tensor의 원소 수로 이전 연구들에서 주로 다뤄지지 않았으나, 하드웨어에 따른 Runtime을 결정하는데 중요 역할을 한다고 주장
Network Complexity
- 최신 모델들이 다양한 연산으로 구성된 층으로 이루어지므로, 복잡도 계산에는 Conv만 고려
-
Normalization, Pooling등은 복잡도의 일부만 차지하고, Conv에 비례함
-
Activation도 Conv와 함께 나타남
-
$w\times r \times r$의 입력을 $w$개의 $k\times k$ Kernel을 가진 Conv에 넣었을 때, Conv의 파라미터들에 따른 계산 복잡도는 다음과 같다.
Metrics Conv $f$ $\underset{O(\text{Input*Weight})}{k^2}\times \underset{\text{# of Input Chans}}{w}\times \underset{\text{# of Kernels}}{w}\times \underset{\text{# of Kernel Operations}}{r^2} \ =w^2 r^2 k^2$ $p$ $\underset{\text {# of Kernel Params}}{(k^2w)}\times \underset{\text {# of Kernels}}{w}=k^2w^2$ $a$ $\underset{\text{# of Kernels}}{w}\times \underset{\text{# of Kernel Operations}}{r^2}=wr^2$ 모델을 키울 때는 $k$는 보통 건드리지 않고 층 수를 키우므로, 위 식의 $k$를 1로 바꾸고 층 수 $d$를 추가
Metrics Conv $f$ $dw^2r^2$ $p$ $dw^2$ $a$ $dwr^2$
-
- 결론적으로 조절할 수 있는 것들은 $d, w, r$이다.
-
이때, Scaling 전략을 단순하게 하기 위해 세 가지를 동일한 조절 값 $s$로 조절한다.
-
Simple Scaling: $d, w, r$ 중 하나만 Scaling
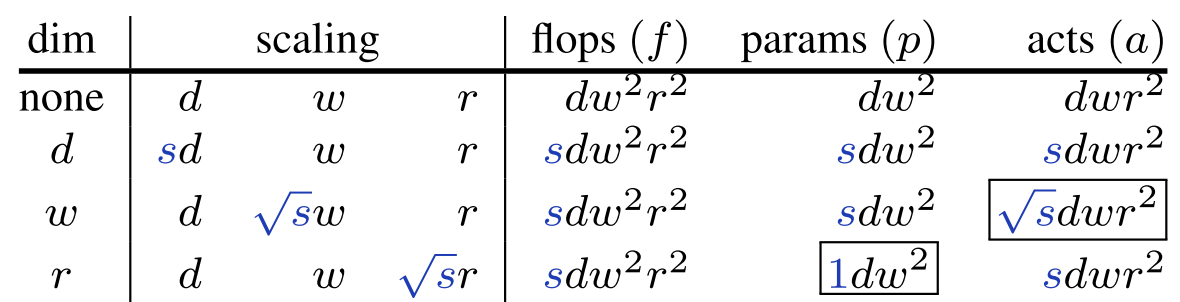
- $w$와 $r$은 증가량에 따라 $f$가 제곱으로 증가하므로 이를 완화하기 위해 $\sqrt s$로 Scaling한다.
- $a$의 경우 $d$와 $r$에서 $s$를 따라 선형적으로 증가하지만 $w$의 경우는 아니다. 그래서, Compound Scaling을 설계했다.
-
Compound Scaling: 여러 조합으로 Scaling
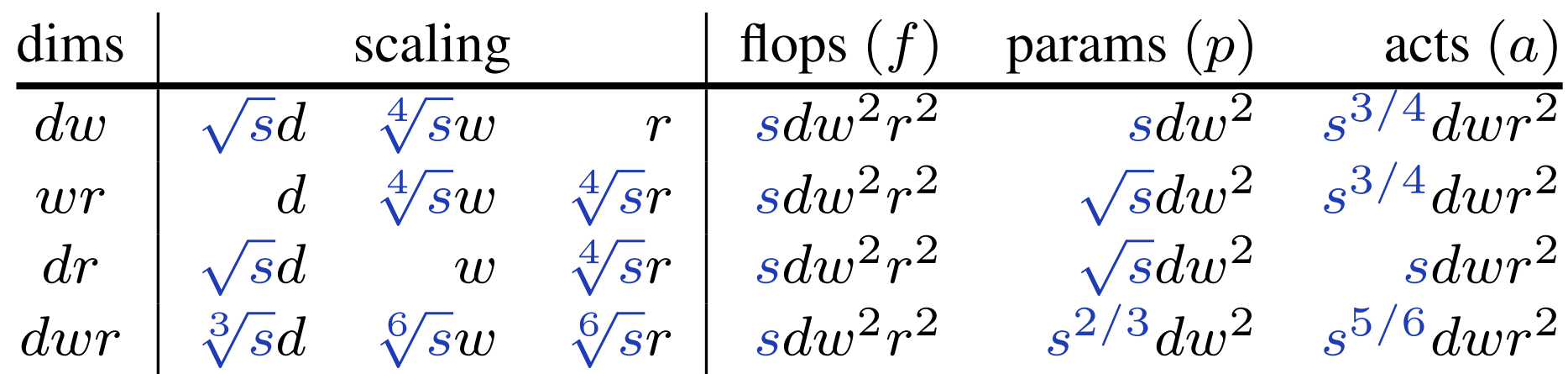
- EfficientNet의 Scaling Factor들의 값 1.2, 1.1, 1.15는 위 표의 $dwr$ Scaling에서 $s=2$인 경우와 유사하다.($\sqrt[3] 2\approx 1.26, \sqrt[6] 2\approx 1.12$)
- $a$가 $s$를 따라 선형에 가깝게 증가한다.
-
Group Width Scaling: 위의 두 경우와 달리 Groupwise Conv를 사용할 경우
Groupwise의 경우 각 Group의 입력 채널 수 $g$가 추가된다. 이 경우도 역시 $k=1$로 둘 수 있다.
Metrics Groupwise Conv $f$ $1\times\underset{\text{# of Group Chans}}{g}\times w\times r^2=wg r^2 $ $p$ $\underset{\text {# of Kernel Params}}{(1^2g)}\times \underset{\text {# of Kernels}}{w}=wg$ $a$ $wr^2$ 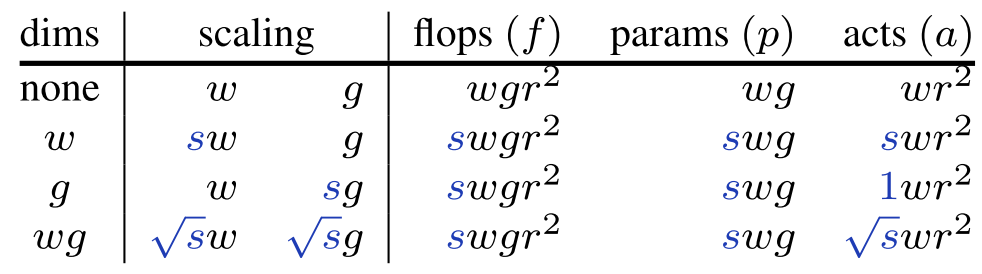
- 많은 모델들이 Groupwise 혹은 Depthwise Conv를 사용하므로, Scaling 방식 설계
-
$wg$를 모두 Scaling할 때가 일반적인 Conv를 Scaling하는 경우와 $f, p, a$ 증가량이 동일하므로 별다른 언급이 없다면 $wg$를 Scaling
그 외 주의점
-
Depthwise Conv를 사용하는 경우는 $g=1$이므로 Scaling하지 않음
-
$g>w$이라면 $g=w$로 두고, $w$가 $g$로 나누어 떨어지도록 반올림
-
-
-
Runtime of Scaled Models
- 위에서 Metric으로 정한 $f, p, a$과 모델 Runtime 사이의 관계를 평가한다. 모든 실험은 PyTorch와 32GB Volta 8대를 이용했다.
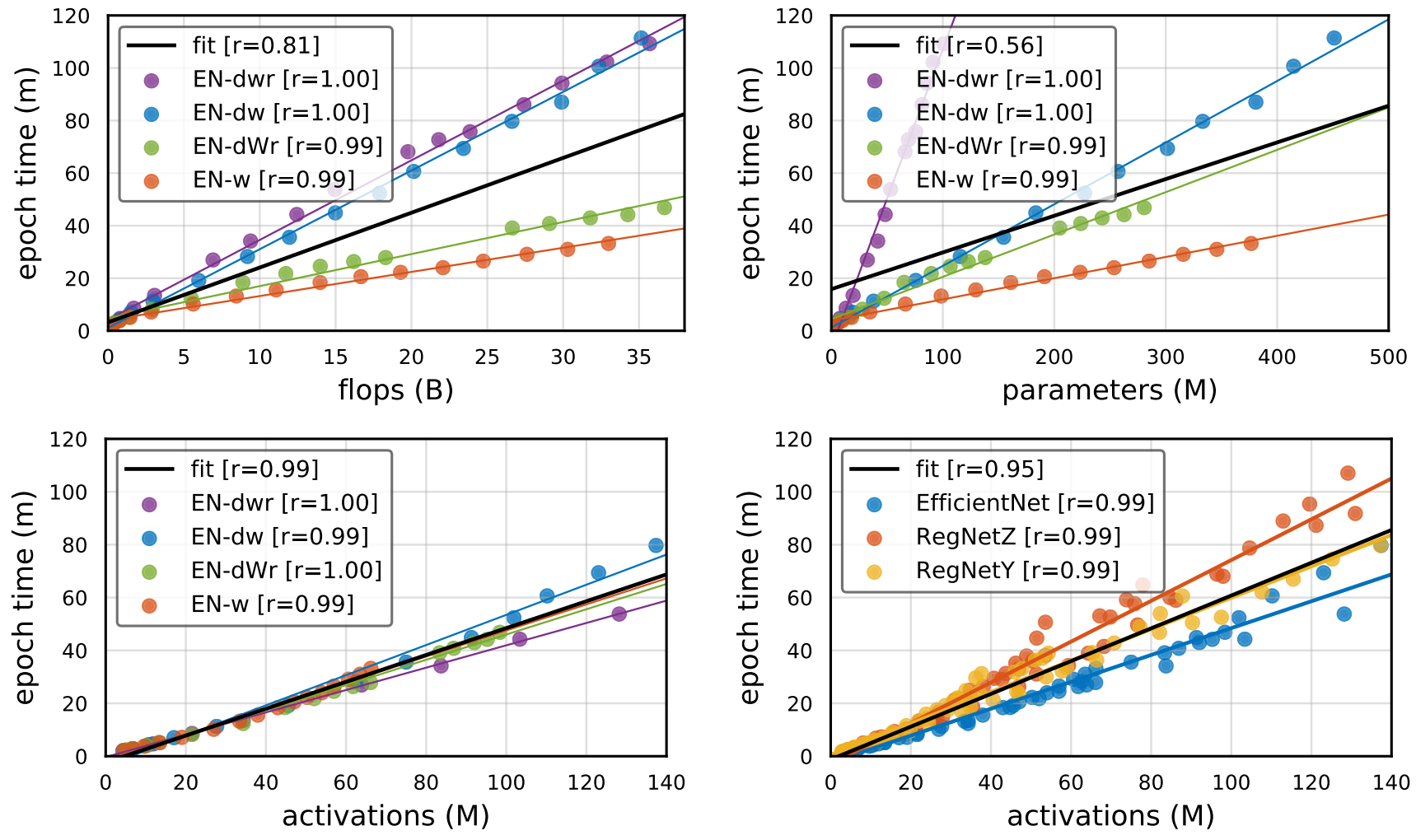
r은 Pearson Correlation을 의미, 검은색 직선 fit은 전체 데이터에 대한 fitting line이다.
- Flops와 Parameters는 Runtime과 상관관계가 적으나, Activations는 거의 1에 가까운 상관관계를 보임
- 물론, Activation의 종류에 따라 다르고 몇몇 큰 모델들은 예측한 것 보다 실행 시간이 더 길었다.
Fast Compound Model Scaling
-
Runtime과 Activation의 상관관계를 확인 했으므로, Model Activation의 증가를 최소화하는 새로운 Scaling 전략을 설계
-
앞의 실험들에서 $w$를 증가시키는게 가장 Activation을 줄였으므로, $w$ 위주로 늘림
-
새로운 하이퍼 파라미터 $\alpha$를 도입해 다음의 값들을 계산
\[e_d=\frac{1-\alpha}{2}, \qquad e_w=\alpha,\qquad e_r=\frac{1-\alpha}{2}\] -
위의 값들을 이용해 $d’, s’, w’$를 구함
\[d'=s^{e_d}d, \qquad w'=\sqrt s^{e_w} w, \qquad r'=\sqrt s^{e_r}r\]Groupwise Conv의 경우 $g’=\sqrt s^{e_g}g$
-
결과적으로 연산량은 다음과 같음
\[f=sdw^2r^2,\qquad p=s^\frac{1+\alpha}{2}dw^2, \qquad a=s^\frac{2-\alpha}{2}dwr^2\] -
$\alpha=1$이면 $w$ Scaling, $0$이면 $dr$ Scaling, $1/3$이면 $dwr$ Scaling이다.
- 흥미로운 부분은 $1/3<\alpha <1$인 부분으로, 이 구간을 $dWr$ Scaling이라고 부르고, 별다른 말이 없으면 $\alpha=0.8$로 둔다.
-
Experiments
- 최대한 공정하고 재현가능한 결과를 얻으면서도 SOTA를 달성하기 위해 다음의 Optimization Setting을 이용
- SGD with Momentum of 0.9, Exponential Learning Rate Scheduler, 5 Epochs of gradual WarmUp
- Label Smoothing with $\epsilon=0.1$, MixUp with $\alpha=0.2$
- AutoAugment, Stochastic Weight Averaging, Mixed Precision Training
-
사용된 모델
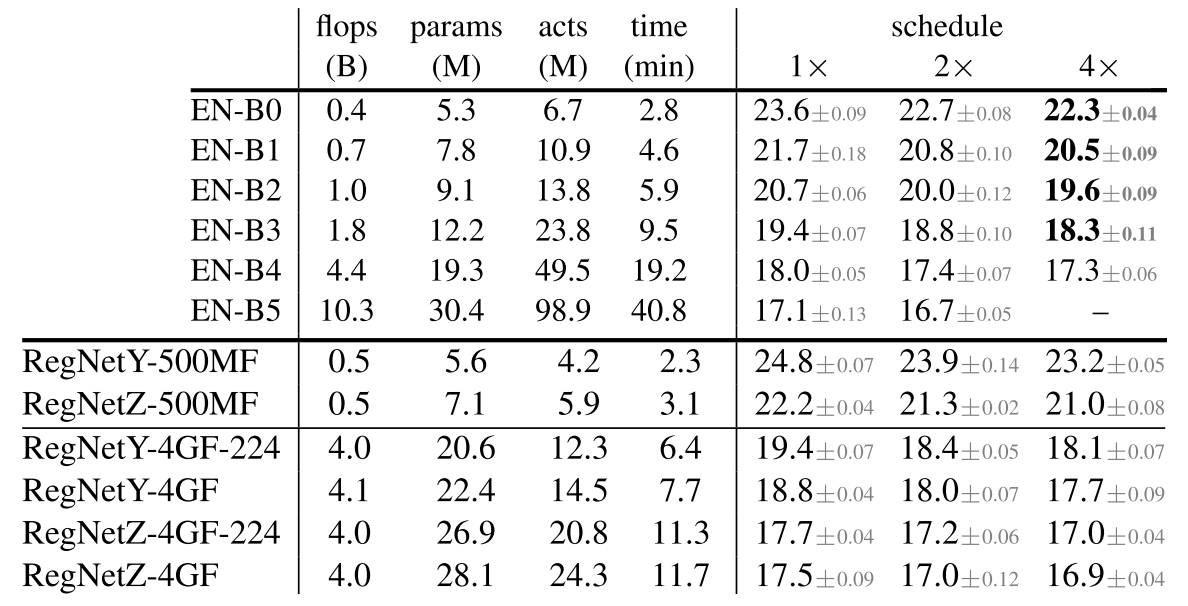
- Schedule은 Epoch 수를 의미($1 \times$는 100 Epoch)
- RegNet-500MF는 해상도를 224로, 4GF 중 표시가 되어있지 않은 것은 Random Search로 찾은 해상도를 사용했다.
Simple and Compound Scaling
-
EfficientNet
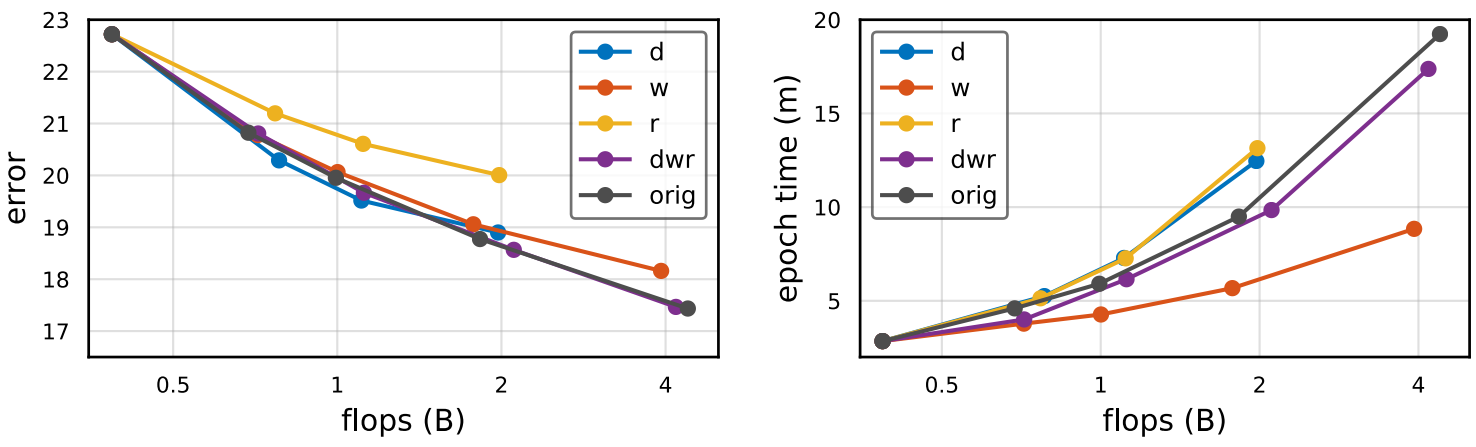
-
RegNetY, RegNetZ
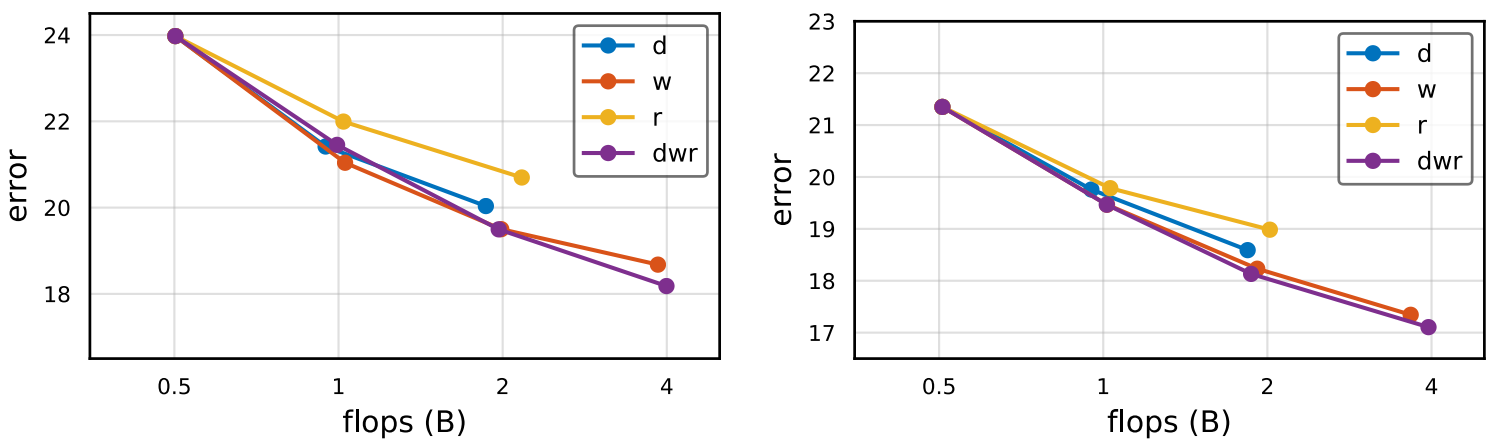
- 두 모델 공통적으로 $dwr$이 성능은 가장 좋지만 Runtime이 크다.
- 앞서 이야기한 것처럼 $w$가 Activations 증가량이 가장 적으므로 Runtime도 짧음을 볼 수 있다.
Fast Scaling
-
EfficientNet
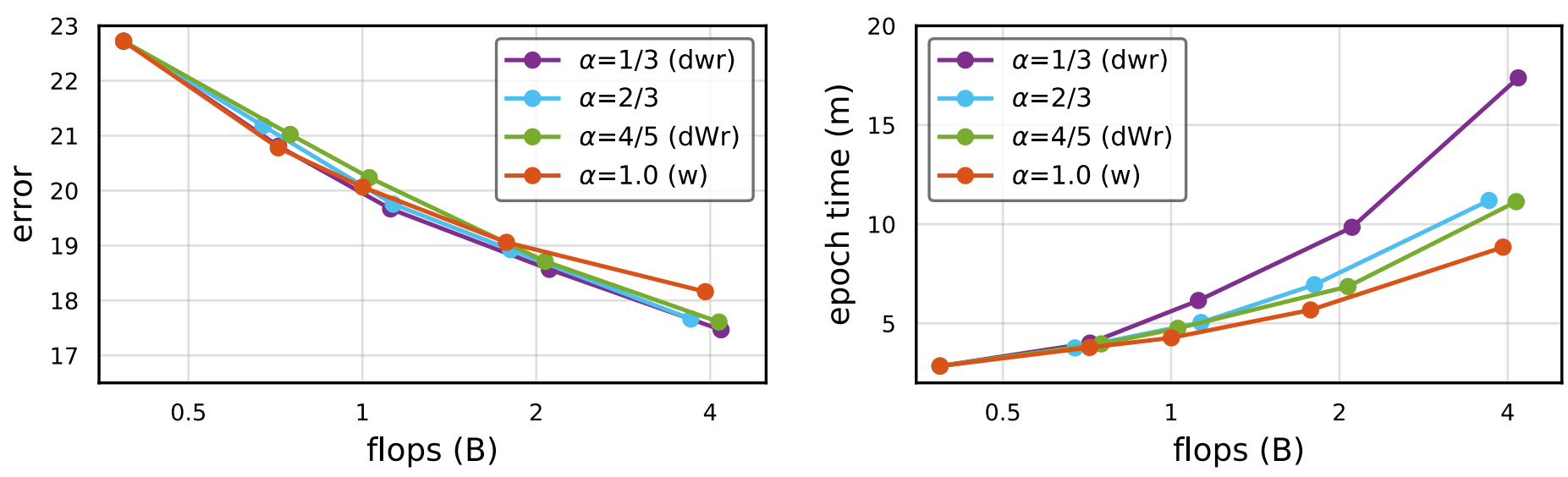
-
RegNetY, RegNetZ
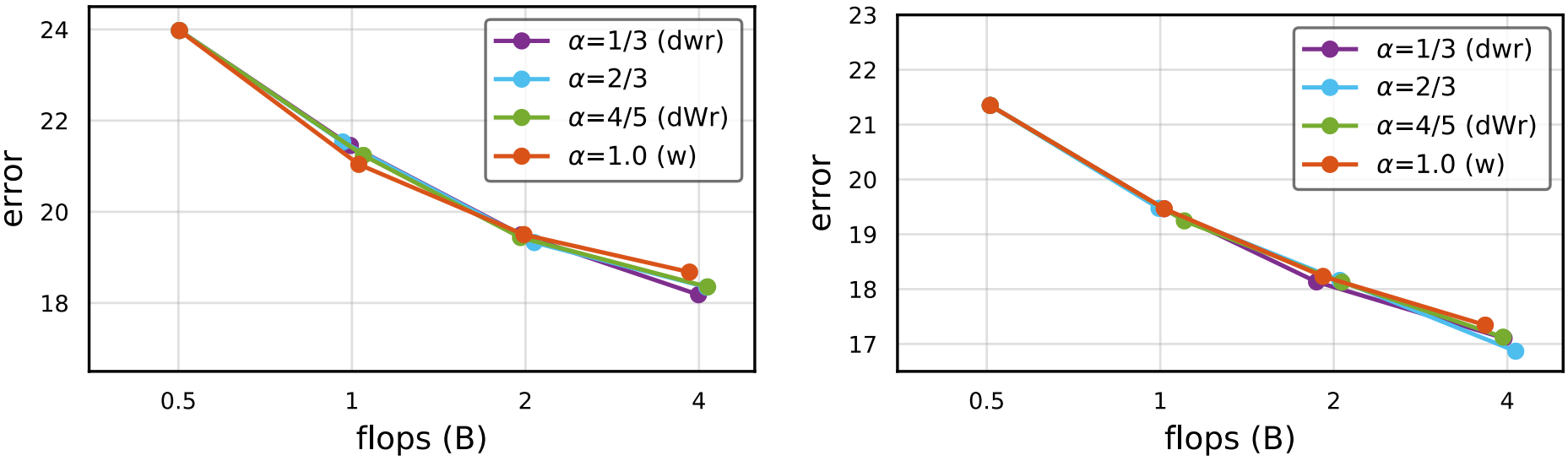
- $\alpha<1$에서가 $w$보다 성능이 더 높고, $\alpha =0.8$인 $dWr$은 $dwr$과 비슷한 성능을 지니면서도 훨씬 낮은 Runtime을 가진다.
- 여러 $\alpha$에 대한 경향성은 모델이 커질수록 증가한다.
- RegNet의 경우 EfficientNet과 달리 Groupwise Conv를 위한 $g$가 1이 아니므로, $w$ Scaling에 의해 $g$도 선형적으로 증가해 EfficientNet보다 $w$ Scaling의 효과가 더 크다.
Scaling versus Search
그런데, 이런 Scaling 과정이 RegNet에서 설계한 Design Space에서 Random Search한 것 보다는 좋아야 의미가 있다. 그래서 Random Search와 Scaling을 비교한다.
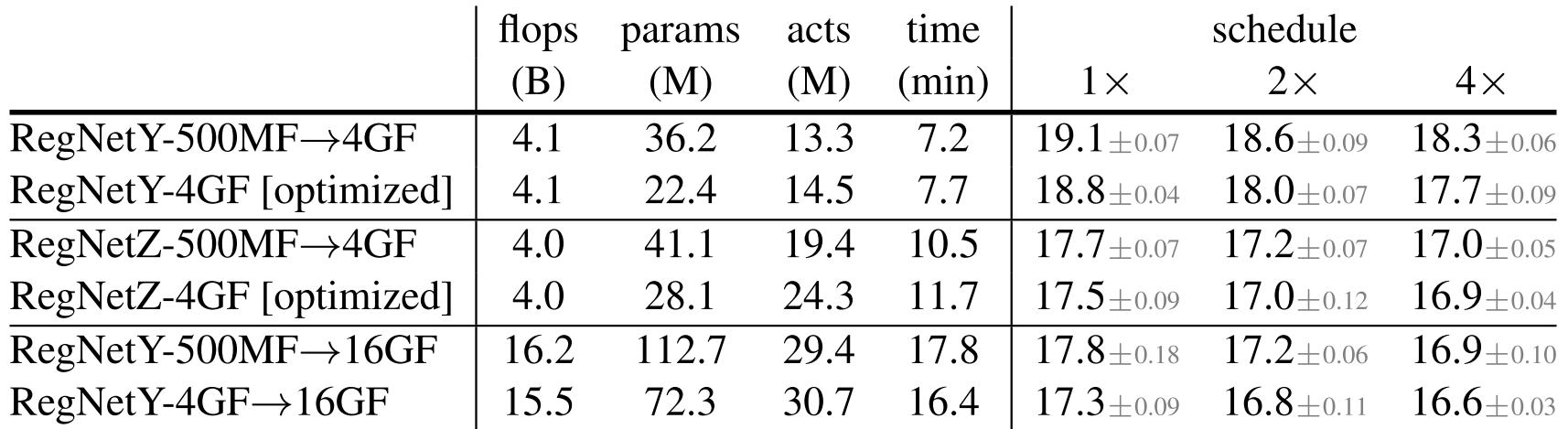
- [optimized]가 Random Search의 결과이다. 이 모델들이 평균적으로 더 적은 파라미터를 가지는데, 이는 각 Stage 안의 Block들을 재배열하지 않고 Scaling 했기 때문이다.
- 5, 6번째 행은 Hybrid Scaling Stategy로 계산 량을 감당할 수 있는 크기의 모델에서 Random Search로 Best Model을 찾고, 이 후 Scaling하는 전략이다.
Comparision of Large Models
Scaling은 Random Search가 불가능한 많은 연산량을 요구하는 모델들을 설계하기 위함이다. 따라서, 모델을 16GF까지 Scaling한 후 결과들을 분석해본다.
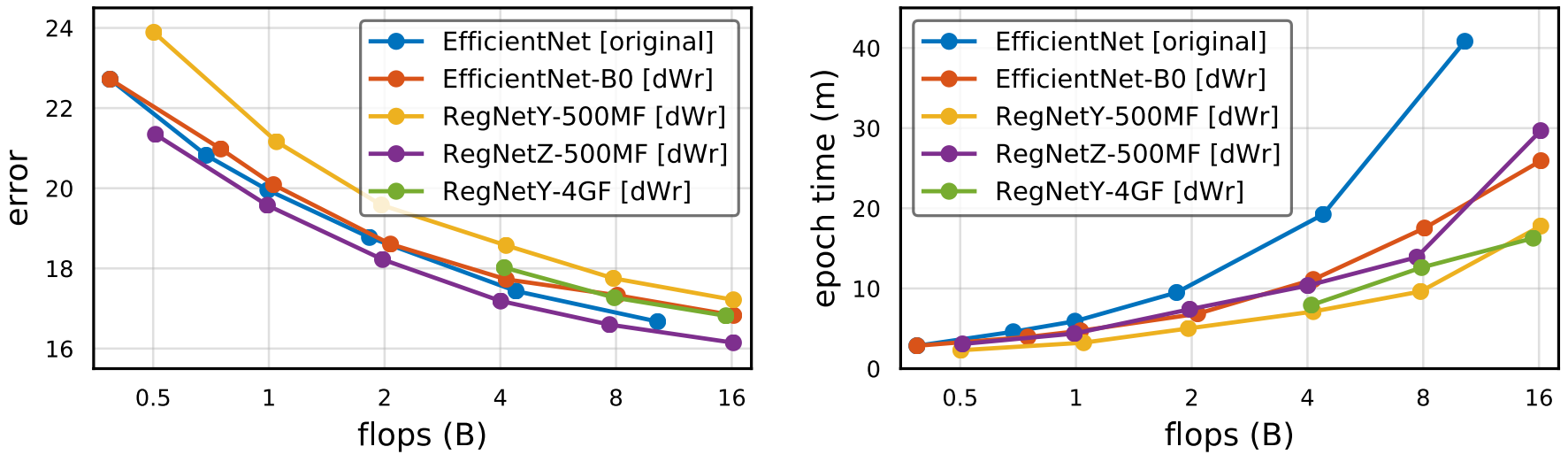
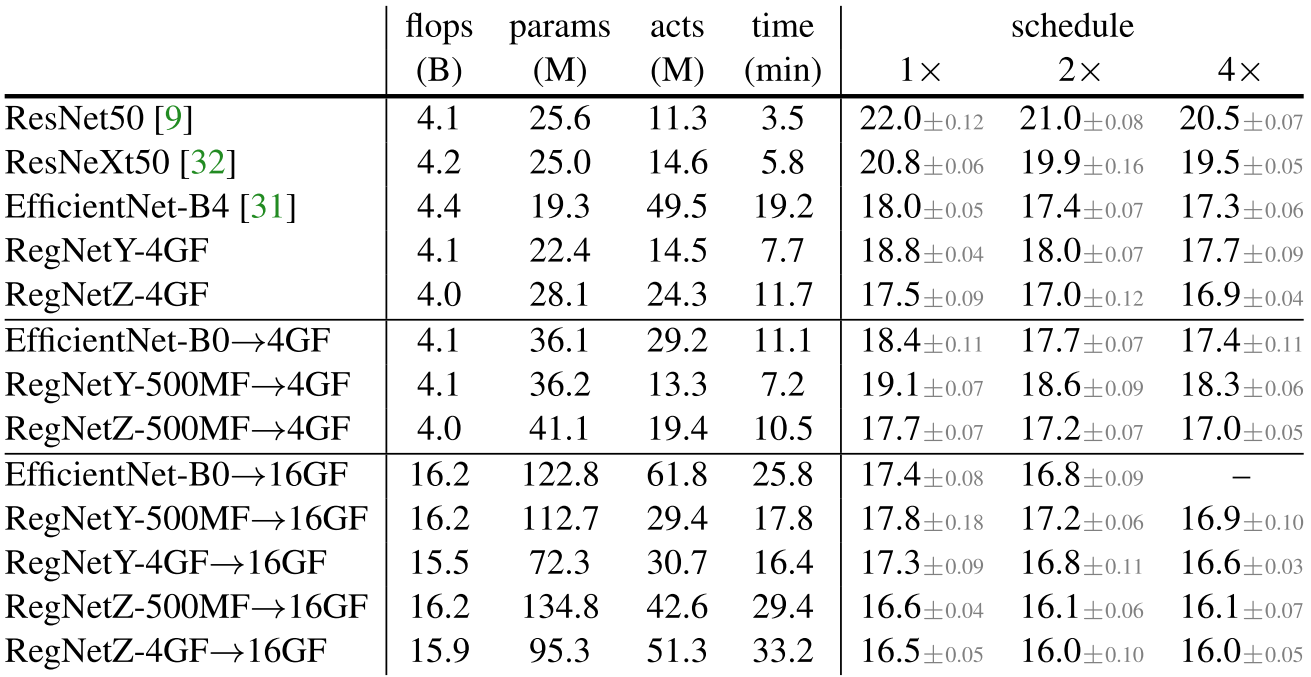
- Scaling한다고 모델의 원 성능 순서가 바뀌지 않음
- $dWr$ Scaling은 Original Scaling보다 Runtime이 줄어듦
- RegNetY-500MF와 RegNetZ-500MF의 성능 차이는 $0.8\%$였는데, $\text{0.5MF}\rightarrow\text{16GF}$ 이후 $2.2\%$로 줄어듦
- Hybrid Strategy를 이용했을 때, $\text{4GF}\rightarrow\text{16GF}$에서 RegNetY와 RegNetZ의 격차가 해소됨
- RegNetY가 높은 Flops의 모델에서 가장 빠른 모델이다.
Discussion
- Activations이 Runtime과 관련 깊음을 보이고, 이를 고려한 새로운 Scaling 방식을 제안

Leave a comment