Fastformer: Additive Attention Can Be All You Need

관련 링크 : https://arxiv.org/abs/2108.09084

Introduction

• Transformer 모델의 핵심은 입력 토큰들 사이의 Context을 모델링하는 Self-Attention이다.
  • 하지만, Self-Attention은 입력 토큰 수의 제곱에 비례하는 시간 복잡도를 가진다.
  • 이를 해결하기 위해 Local Attention의 조합을 이용한 Sparse Attention이 등장했으나, Global Context를 제대로 모델링 하지 못 했다.
  • 다른 대안으로 제안된 Linformer는 Self-Attention을 근사하기 위해 Key와 Value를 저차원 행렬로 Project했으나, Context-Agnostic했다.
  • 그리고 이 대안들은 토큰 수가 많을 때 효과적이지 않았다.
• 그래서, Fastformer를 제안한다.
  1. Query Matrix를 Global Query Vector로 줄인다.
  2. Key Matrix와 Query Vector간에 Element-wise Product를 수행해 이를 Global Key Vector로 만든다.
  3. Global Key Vector와 Value Matrix를 Element-wise Product시켜 새로운 Value Matrix를 얻는다.
  4. 새로운 Value Matrix를 선형 변환해 Context-aware Attn Matrix를 얻는다.
  5. Context-aware Attn Matrix와 Query Matrix를 더해 최종 결과를 얻는다.

Fastformer

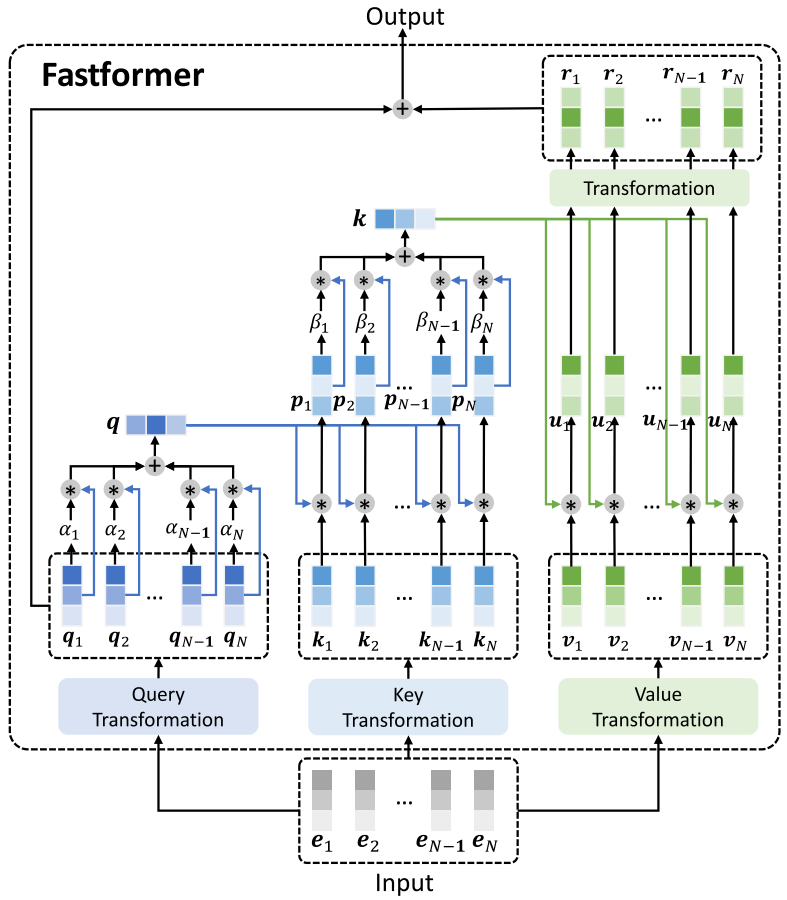
입력 행렬을 $\mathbf E \in \mathbb R^{N\times d}$이고, $[\mathbf e_1, \mathbf e_2, \ldots ,\mathbf e_N]$이라 표현하자.

1. $\mathbf E$에 독립적인 선형 변환을 적용해 $\mathbf Q, \mathbf K, \mathbf V \in \mathbb R^{N\times d}$를 얻는다. 각 행렬은 $[\mathbf q_1, \mathbf q_2, \ldots ,\mathbf q_N]$, $[\mathbf k_1, \mathbf k_2, \ldots ,\mathbf k_N]$, $[\mathbf v_1, \mathbf v_2, \ldots ,\mathbf v_N]$로 표현 할 수 있다.

   실제 구현에서 $\mathbf Q$와 $\mathbf V$는 동일하다. 따라서, 기존 Transformer가 $\mathbf Q, \mathbf K, \mathbf V$ 변환과 Attention 이후 행렬 연산으로 $4\times \underset{\text{Head 수}}{h} \times \underset{\text{임베딩 차원}}{d}$ 제곱의 파라미터를 가졌다면, Fastformer는 $3hd^2+2h\times\underset{\mathbf w_{q, k}}{d}$ 만큼의 파라미터를 가진다.

2. $\mathbf Q$를 이용해 Global Contextual Information을 담은 Global Query Vector $\mathbf q \in \mathbb R^{d}$를 얻는다.

   \[\mathbf q =\sum^N_{i=1} \alpha_i\mathbf q_i\qquad(O(N\cdot d))\]

   • $\alpha_i$는 Learnable Vector $\mathbf w_q \in \mathbb R^d$를 이용하여 계산한다. Head 개수만큼 존재하므로, $hd$개의 파라미터를 가진다.

     \[\alpha_i=\frac{\exp(\mathbf w_q^T \mathbf q_i/\sqrt d)}{\sum^N_{j=1}\exp(\mathbf w_q^T \mathbf q_j/\sqrt d)}\]

3. $\mathbf q$와 $\mathbf V$간의 Element-wise Product를 통해 Global Key Vector를 만든다.

   • 먼저 $\mathbf q$와 $\mathbf V$의 각 벡터를 이용해 $\mathbf p$를 얻는다.

     \[\mathbf p_i = \mathbf q * \mathbf k_i \qquad(O(d))\]
     • $*$는 Element-wise Product를 의미한다.

     Concat하면 $\mathbf q$의 영향이 $\mathbf V$의 각 벡터에 동일하게 적용되므로, Context 이해에 좋지 않아 더해준다.

   • Global Key Vector $\mathbf k \in \mathbb R^d$를 얻는다.

     \[\mathbf k =\sum^N_{i=1} \beta_i\mathbf p_i\qquad(O(N\cdot d))\]

     • $\beta_i$는 Learnable Vector $\mathbf w_k \in \mathbb R^d$를 이용하여 계산한다. Head 개수만큼 존재하므로, $hd$개의 파라미터를 가진다.

       \[\beta_i=\frac{\exp(\mathbf w_k^T \mathbf p_i/\sqrt d)}{\sum^N_{j=1}\exp(\mathbf w_k^T \mathbf p_j/\sqrt d)}\]

4. $\mathbf k$와 $\mathbf V$간의 Element-wise Product와 선형 변환으로 Context-Aware Attn Matrix $\mathbf R\in\mathbb R^{N\times d}$를 얻는다.

   • Element-wise Product로 새로운 Value Matrix $\mathbf U=[\mathbf u_1, \mathbf u_2, \ldots, \mathbf u_n]$을 얻는다.

     \[\mathbf u_i = \mathbf k * \mathbf v_i\qquad(O(d))\]

   • 선형 변환($\mathbb R:d \rightarrow d$)을 통해 Context-Aware Attn Matrix $\mathbf R=[\mathbf r_1, \mathbf r_2, \ldots , \mathbf r_n]$을 얻는다.

5. $\mathbf R$과 $\mathbf Q$를 더해 Fastformer의 최종 출력을 얻는다.

추가적으로, Albert에서 영감받은 Cross-Layer Parameter Sharing도 사용한다. 간단히, 각 층의 Self-Attention Layer의 파라미터만 공유하는 방식이라 생각하면 된다.

Experiments

Datasets and Tasks

• Amazon, IMDB: 리뷰에 따른 평점 예측
• MIND: 기사 내용에 따른 주제 분류/이전 클릭 기록으로 추론한 기사 추천
• CNN/DailyMail: 문서 요약
• PubMed: 위 데이터셋 보다 긴 문장 요약

Effectiveness Comparison

• Sentiment and Topic Classification

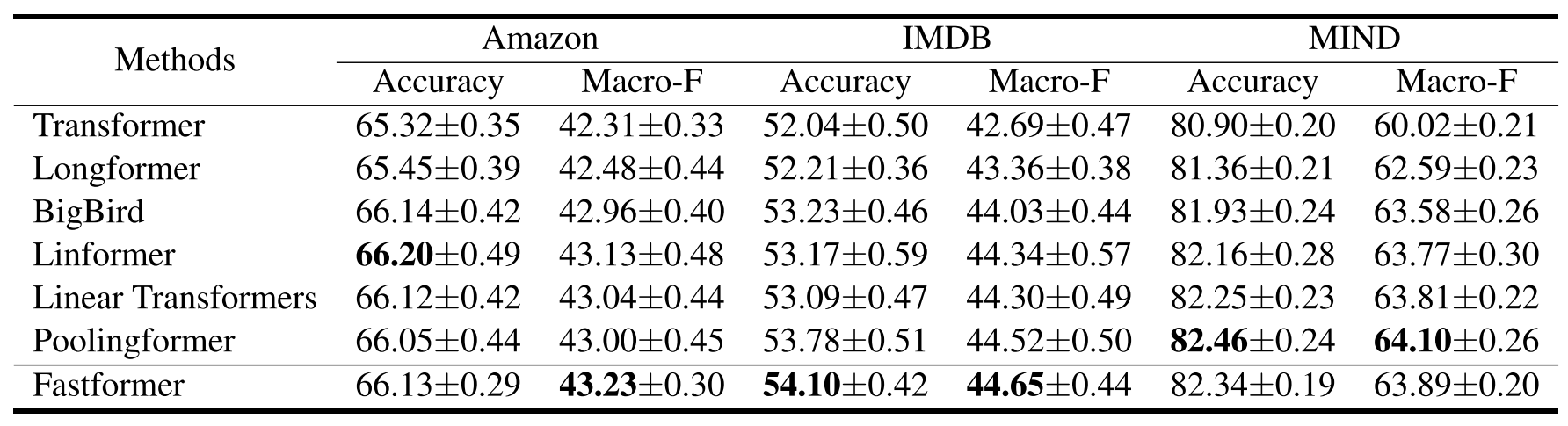
• News Recommendation using MIND

  

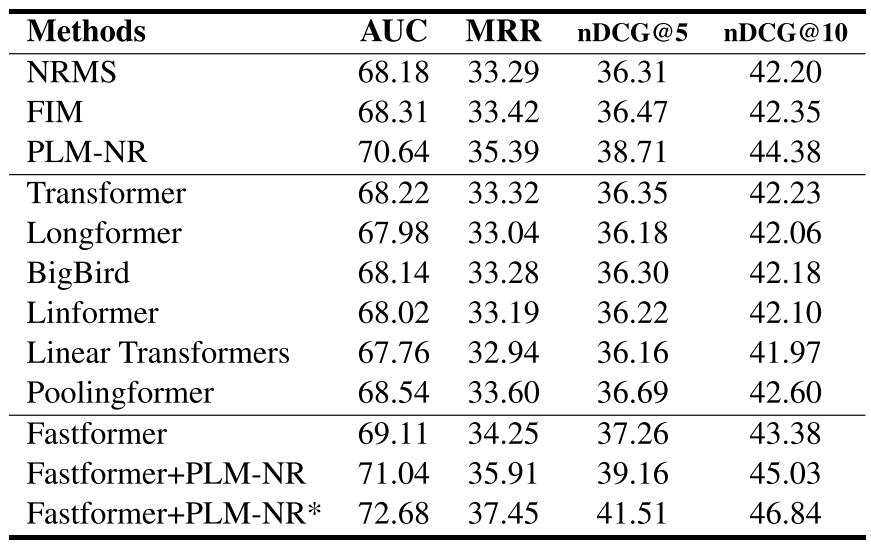
  • $*$는 앙상블로, 최고 성능을 보인다.

• Text Summarization

  

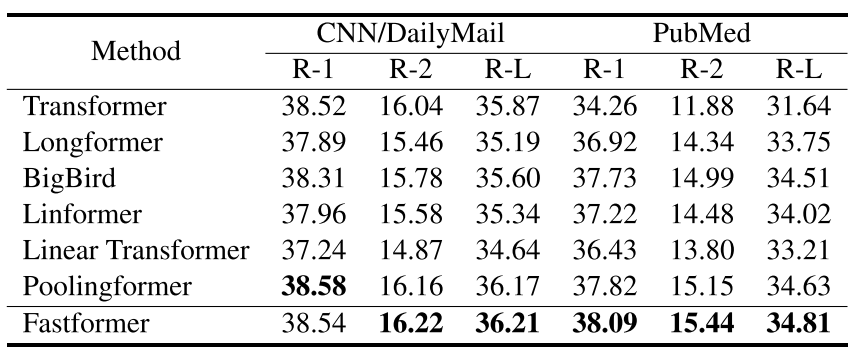
  • CNN/DM이 상대적으로 짧은 문장들로 이루어 져서 PubMed보다 Fastformer의 효과가 적지만 그럼에도 좋은 성능을 보인다.

Efficiency Comparision

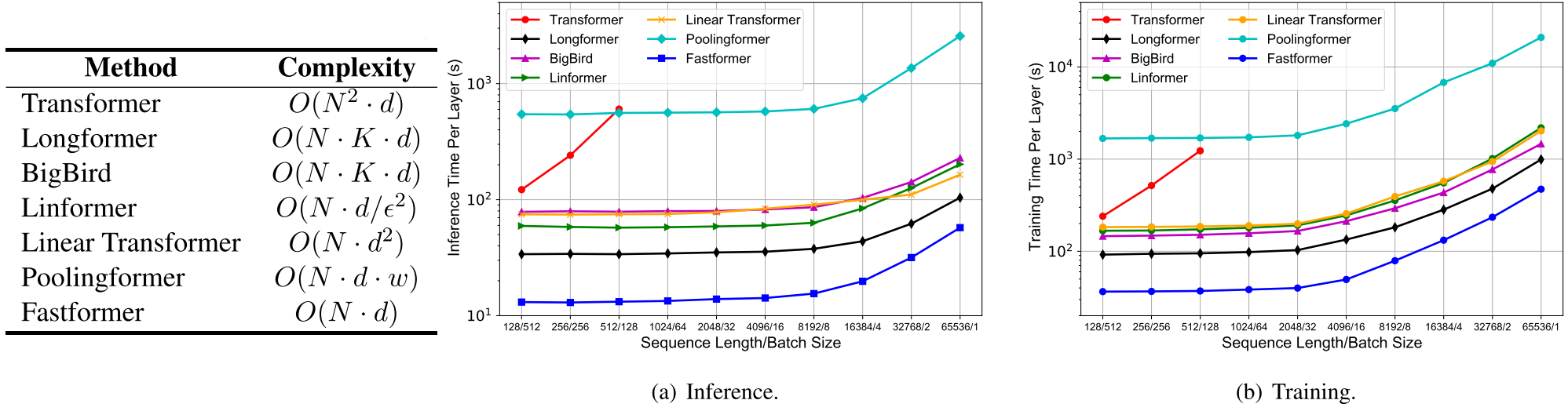
• 이론적인 계산 복잡도도 가장 낮고, 실제로도 가장 Runtime이 짧다.

Influence of Interaction Function

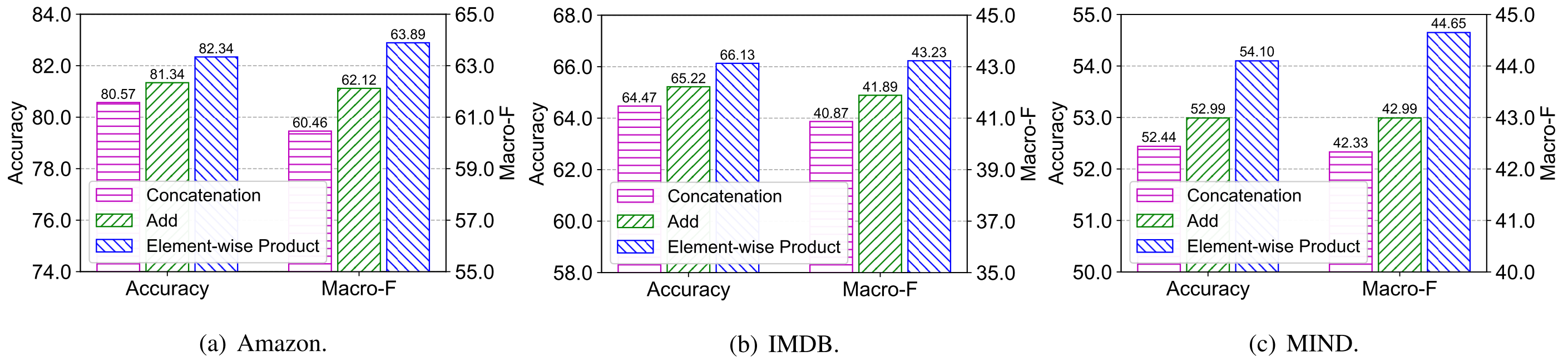
• $\mathbf q,$ $\mathbf k$와 $\mathbf Q, \mathbf K$ 간의 Interaction은 앞서 제안한 Element-wise Product 외에도 Concat과 Add가 가능하다.
  • Concat은 값에 변화를 주지 않으므로 Interaction을 의미하지 않아 성능이 가장 낮다.
  • Add는 선형 관계만을 근사할 수 있으므로 Concat보다 좋으나 Element-wise Product보다는 나쁘다.

Influence of Parameter Sharing

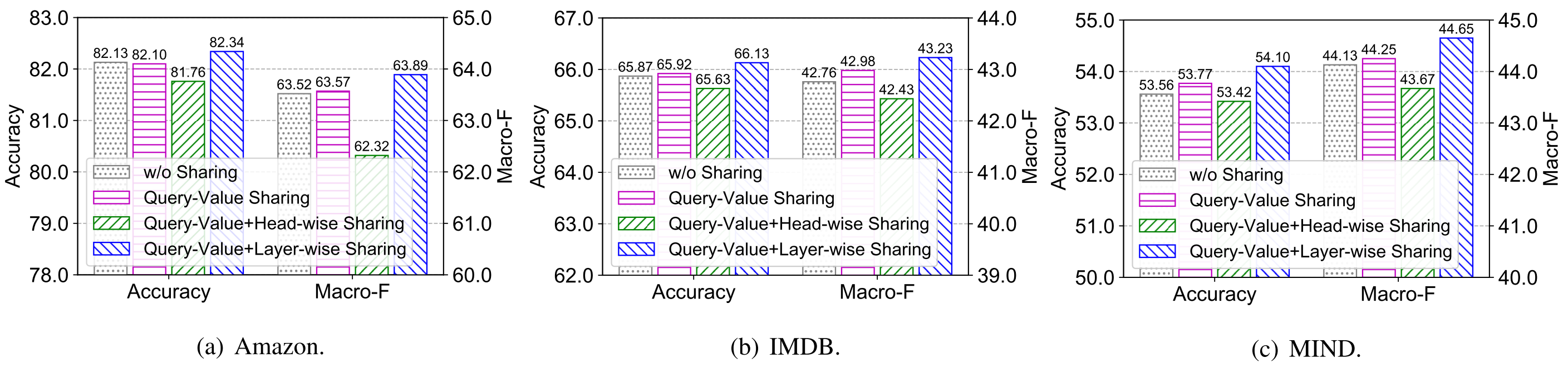
• $\mathbf Q$와 $\mathbf V$를 공유하는 방식은 약간의 성능 향상을 가져왔다.
• Head-wise Sharing은 여러 Head들이 동일한 파라미터를 공유하는 방식인데, 애초에 Head를 여러개 쓰는 것은 각 Head가 다른 Context를 파악하도록 하기 위함이므로 이를 공유하니 성능이 하락했다.
• Albert의 Layer-wise Sharing은 성능 향상을 가져왔다.

Applications of Fastformer

• Binary Classification Task로 Transfer시 성능 측정

  

Conclusion

• 선형 시간복잡도로 많은 토큰 수를 다룰 수 있는 Additive Attention을 이용한 Fastformer를 제안

Remarks

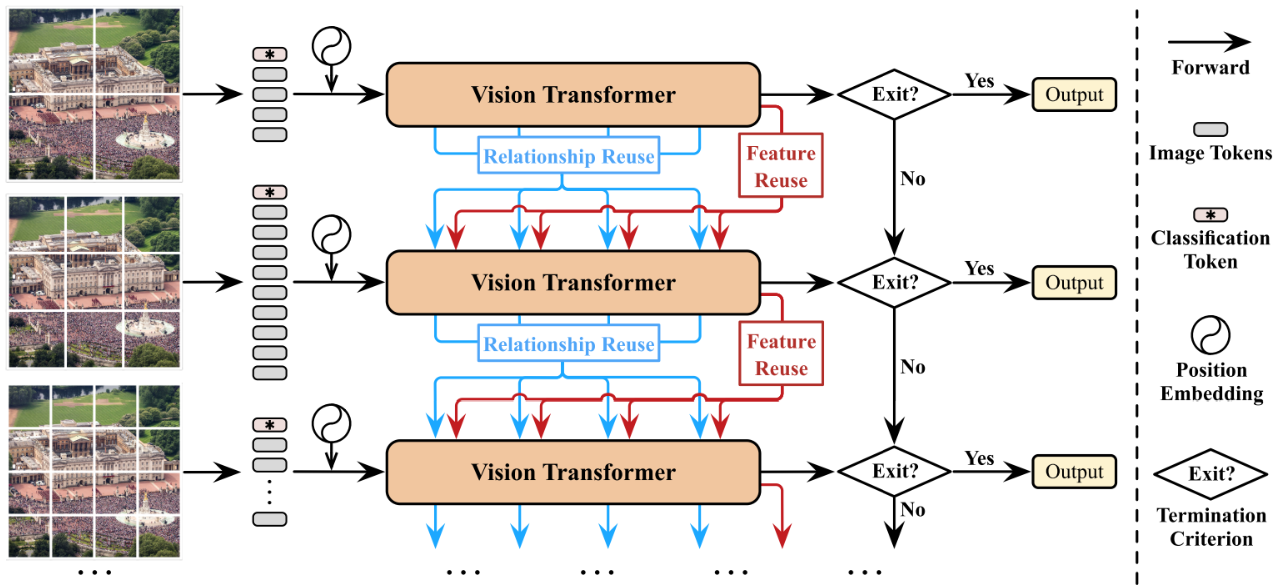
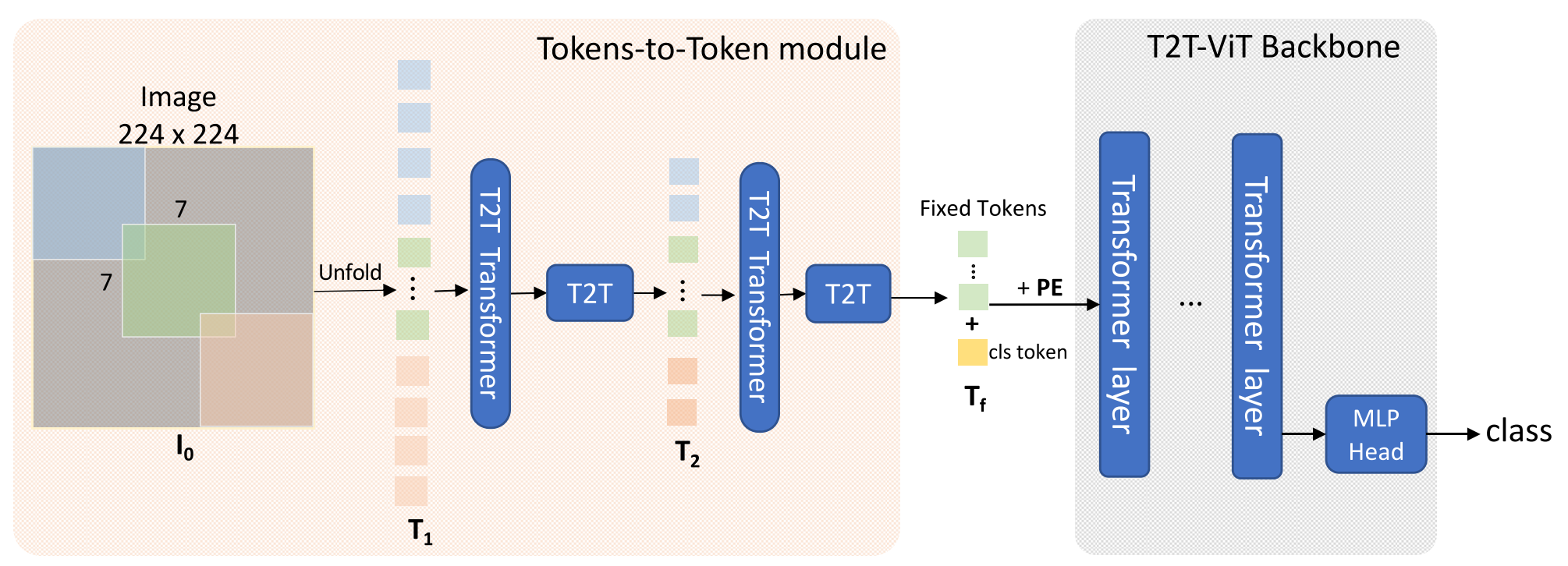
자연어에 비해 상대적으로 토큰 수가 작은 Vision Task에도 Fastformer가 효과적일지 궁금하다.