Learning Representations by Maximizing Mutual Information Across Views

관련 링크 : https://arxiv.org/abs/1906.00910

Self-Supervised Learning : AMDIM(2019)

Abstract

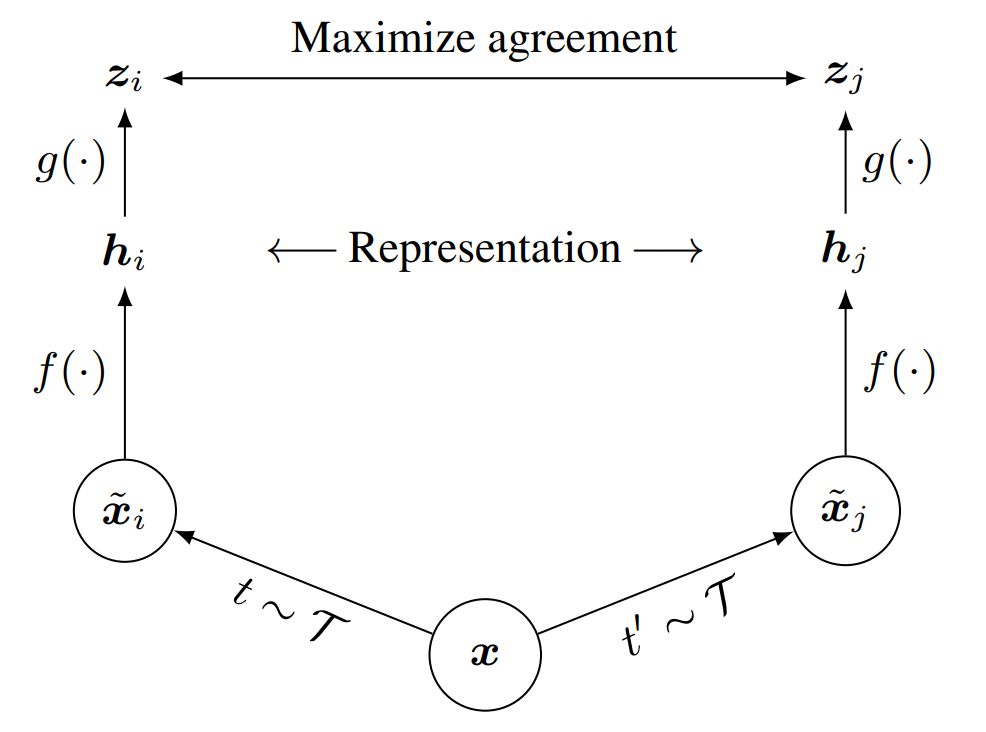
Shared context를 가진 view로부터 뽑아낸 feature 사이에 mutual information을 극대화 하는 self-supervised learning 방식을 제안한다. Context란 다른 위치(카메라의 위치)나 다른 형태(촉각, 청각, 시각) 같은 multiple view에도 영향을 주는 정보로 물체의 존재나 사건의 발생등을 의미한다.

1. Introduction

사람은 쿠키의 맛에 대해 생각할때 제빵 광경, 쿠키의 향기, 구워지는 소리등 어느정도 관련성 있는 경험을 떠올린다. 이는 모든 경험이 쿠키에 관련되어 있기 떄문이다. 이미지의 관점에서 관련된 경험은 data augmentation이 적용된 이미지, 쿠키는 context이다. 본 논문의 핵심 아이디어는 관련된 경험들에서 가져온 feature들의 mutual information를 극대화하면 feature가 ‘쿠키’라는 context에 영향을 받는 higher-level factor에 대한 정보를 학습한다는 것이다.

이를 위해 Local Deep InfoMax를 이용한다. 기존의 Local DIM은 이미지 전체를 뜻하는 global summary feature vector와 encoder 중간층의 collection of local feature vector의 mutual information을 극대화 했는데, 본 논문은 이를 개량해 이용한다. 자세한 변경점은 3장에서 논한다.

다양한 데이터셋에서 성능을 측정했고, 상당히 좋은 성능을 보였다. 자세한 결과는 4장에서 논한다.

2. Related Work

• Pretext task : AMDIM은 데이터에서 의미있는 정보를 만들기 위해 pretext task를 만들어 접근하는 기존 방식과 다르다.
  • Pretext task Approach : Auto-Encoder/Rotation/Colorization/Jigsaw
  • Mutual Information Approach : CPC/NCE/Tracking emerges by colorizing videos
• Evaluation Protocol : 모델 구조에 의한 성능 향상은 제외하기 위해 아래 논문들의 방식을 따른다.
  • Revisiting SSL/Scaling and benchmarking SSL

3. Method Description

본 논문이 제안하는 방식은 Augmented Multiscale DIM로, Deep InfoMax를 개량한다.

• 하나의 이미지가 아닌 augmented 이미지쌍들에서 뽑은 feature들간에 mutual information을 극대화한다.
• 하나의 global, local scale로 비교하지 않고 다양한 scale 사이의 mutual information을 극대화한다.
• 더욱 성능이 좋은 encoder를 사용한다.
• Mixture-based representation을 도입한다.

3.1 Local DIM

$p(f_1(x))$, $p(f_7(x)_{ij})$와 $p(f_1(x),f_7(x)_{ij})$가 주어졌을때 local DIM는 $p(f_1(x),f_7(x)_{ij})$에서 $I(f_1(x);f_7(x)_{ij})$를 최대화하는 encoder $f$를 찾는다. Mutual information은 직관적으로 $f_1(x)$을 모를 때보다 알 때 $f_7(x)$를 추측할 수 있는 정도를 의미한다.

$f_1$없이 $f_7$을 예측하는 절대적인 예측능력을 학습시키는 것은 모든 데이터를 유사한 값으로 예측하는 degenerate representation 문제에 취약하다. Local DIM은 $f_1$을 기준으로 $f_7$을 예측하는 것이므로 상대적인 예측능력이라 볼 수 있어 어느정도 위 문제를 해결할 수 있다.

• 첨자 $d\in \{1, 7\}$ : spatial dimension이 $d\times d$인 레이어임을 뜻한다.

• $i$, $j$ : $d \times d$에서 각 차원의 index를 뜻한다.

  Local DIM에서 $f_1$은 gloabl feature이므로 encoder의 최종 출력이라 $d=1$이고, $f_7$은 local feature이므로 encoder의 중간층 feature map이라 $d=7$이다. AMDIM에서는 global과 local만 비교하지 않으므로, global은 antecedent, local은 consequent로 명명한다.

• $p(f(x))$ : 각 레이어 $f$의 marginal distribution

• $I(x, y)$ : $x$와 $y$의 mutual information

3.2 Noise-Contrastive Estimation

Local DIM 을 사용했을때 mutual information의 하한을 NCE로 사용하면 성능이 가장 좋다. 따라서 NCE의 하한을 최대화하기 위해 다음 loss를 최소화한다.

\[\underset{(f_1(x),f_7(x)_{ij})}{\mathbb E}\left[\underset{N_7}{\mathbb E}[\mathcal L_\Phi(f_1(x),f_7(x)_{ij},N_7)] \right] \tag 1\]

• $N_7$ : negative samples from $p(f_7(x)_{ij})$, $|N_7|\gg 10000$

• $(f_1(x),f_7(x)_{ij})$ : positive sample pair from $p(f_1(x),f_7(x)_{ij})$

• \[\mathcal L_\Phi(f_1,f_7,N_7)=-\log\frac {\exp(\Phi(f_1,f_7))}{\sum_{\tilde{f_7}\in N_7\cup \{f_7\}}\exp(\Phi(f_1,\tilde {f_7}))} \tag 2\]

  • Matching Scores : $$ \Phi(f_1(x),f_7(x)_{ij}) \triangleq \phi_1(f_1(x))^\top \phi_7(f_7(x)_{ij}) \tag 3 $$

    • $\phi_1$/$\phi_7$ : non-linearly transform input to some other vector space

Mutual information을 직접 계산하긴 어렵다. 따라서 이의 하한을 극대화 시키는 방식으로 모델을 학습시킨다.

3.3 Efficient NCE Computation

식 (1)을 이용해 하한을 계산할때 matching scores에서는 non-linearly trasnform을 사용한다. 이는 충분한 고차원 벡터 공간을 고려할 때, 원칙적으로 우리는 선형 평가를 통해 우리가 관심을 갖는 모든 함수를 근사할 수 있어야 하므로 가능하다. 선형 평가의 장점은 Reproducing Kernel Hilbert Spaces(RKHS)를 생각해보면 이해할 수 있지만, 이전 연구들에서 벡터 공간이 유한 차원에서 모델이 표현할 수 있는 변환의 수준을 제한한다는 단점이 있다.

RKHS에 대해 더 공부하고 다시 봐야 할듯

mini-batch안의 $n_a$개의 이미지들이 있을때 NCE 하한 계산을 위한 pseudo-code이다. $s_{exp}=\exp(s-s_{shift})$를 통해 $s$의 요소들은 1과 0사이의 수로 바뀐다. $s-s_{shift}$는 $\log(s_{exp})$로 볼 수 있으므로 최종적인 $s_{nce}=\log(\frac {s_{exp}}{s_{exp}+s_{other}})$이므로 $\ell_{nce}$는 식 (2)와 유사하다.

NCE loss는 데이터셋이 어려울수록 불안정성이 높아지므로, 이를 해결하기 위해 몇가지 방법을 도입한다.

• Regularization

  \[\lambda(\phi_1(f_1(x))^\top\phi_7(f_7(x)_{ij})^2\]
  • 모든 실험에서 $\lambda = 4\times 10^{-2}$를 사용한다.

• Soft clipping non-linearity : $s’=c\tanh(\frac {s}{c})$

  • 식 (2)와 (3) 사이에 적용, 모든 실험에서 $c=20$을 사용

3.4 Data Augmentation

앞서 언급했듯 각 입력의 augmented view의 feature 사이의 mutual information을 최대화 시킨다. 즉 $p_{\mathcal A}(f_1(x^1))$, $p_{\mathcal A}(f_7(x^2)_{ij})$와 $p_{\mathcal A}(f_1(x^1),f_7(x^2)_{ij})$가 주어졌을때 $I(f_1(x);f_7(x)_{ij})$를 최대화하고, 식 (1)를 다음과 같이 바꾼다.

\[\underset{(f_1(x^1),f_7(x^2)_{ij})}{\mathbb E}\left[\underset{N_7}{\mathbb E}[\mathcal L_\Phi(f_1(x^1),f_7(x^2)_{ij},N_7)] \right] \tag 4\]

• $x^1, x^2\sim \mathcal A(x)$ : $\mathcal A(x)$는 입력 $x$에 무작위로 data augmentation을 적용하면 만들어지는 이미지들의 분포
• $N_7$ : negative samples from $p_{\mathcal A}(f_7(x^2)_{ij})$

• $(f_1(x^1),f_7(x^2)_{ij})$ : positive sample pair from $p(f_1(x^1),f_7(x^2)_{ij})$

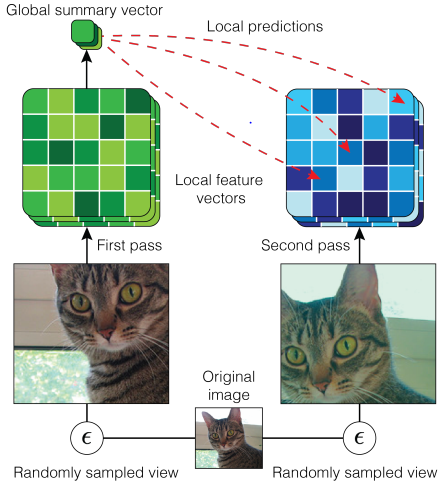
3.5 Multiscale Mutual Information

기존 방식과 달리 multiple feature scale간의 mutual information을 최대화한다. 따라서 \(f_5(x)_{ij}\)를 추가로 도입하여 여러 종류의 joint distribution을 만들고 식 (4)를 다음과 같이 바꾼다.

\[\underset{(f_n(x^1)_{ij},f_m(x^2)_{kl})}{\mathbb E}\left[\underset{N_m}{\mathbb E}[\mathcal L_\Phi(f_n(x^1)_{ij},f_m(x^2)_{kl},N_m)] \right] \tag 5\]

• $N_m$ : negative samples from $p_{\mathcal A}(f_m(x^2)_{ij})$

• $(f_n(x^1)_{ij},f_m(x^2)_{kl})$ : positive sample pair from $p(f_n(x^1)_{ij},f_m(x^2)_{kl})$, $n,m \in \{1,5,7\}$

  • 논문에서는 $(n,m)\in\{(1,5),(1,7),(5,5)\}$를 모두 이용한다.

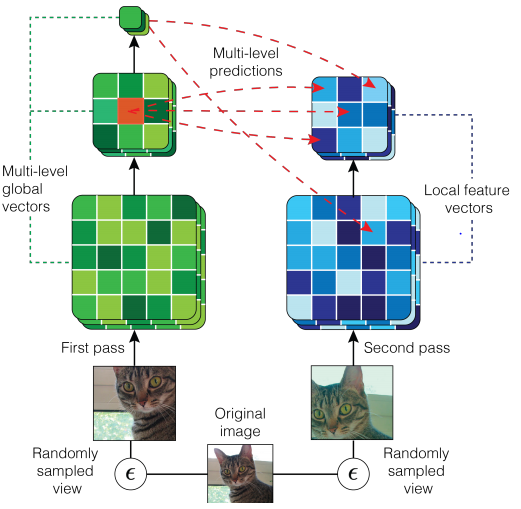
3.6 Encoder

표준적인 ResNet을 사용하지만 DIM에 맞게 몇몇 부분을 수정한다.

• Positive sample pair에서 receptive field가 너무 겹치면 task가 너무 쉬워지고, Padding을 하면 feature distribution이 바뀐다.
  • 각 $\mathrm{ResBlock}$의 첫 번째 층을 1이아닌 $w$와 $s$를 가진 $\mathrm{MeanPool}$을 적용시키고 나머지 층을 $1\times 1\;\mathrm{Conv}$를 사용해 receptive field의 크기를 제한하면서 padding을 사용하지 않도록 만든다.

괄호안의 순서는 (input dim, output dim, kernel width, stride, padding/block depth)를 의미한다. 제일 마지막만 $\mathrm{Conv2d}$인지 $\mathrm{ResBlock}$인지에 따라 다르다. Matching score를 위해 $\phi(f_d)$들은 같은 크기를 가져야 하므로, $f_7$과 $f_5$를 MLP에 집어넣어 크기를 맞춰준다.

3.7 Mixture-Based Representations

$f_1$과 하나의 $\mathrm {ReLU}$와 residual connection을 가진 $\mathrm {FCL}$인 $m_k$를 이용하여 mixture features $\{f^1_1,\ldots,f^k_1 \}$를 만들고 이를 이용해 mixture representation을 도입한다. 따라서 (5)식은 다음과 같이 바뀐다.

\[\underset{f,q}{\mathrm{maximize}}\underset{(x^1,x^2)}{\mathbb E}\left[\frac {1}{n_c}\sum^{n_c}_{i=1}\sum^k_{j=1}\left(q(f^j_1(x^1)|f_7^i(x^2))s_{nce}(f^j_1(x^1),f^i_j(x^2))+\alpha H(q)\right) \right] \tag 6\]

• Optimal distribution $q$ :

  \[q(f^j_1|f^i_7)=\frac {\exp(\tau s_{nce}(f^j_1,f^i_7))}{\sum_{j'}\exp(\tau s_{nce}(f_1^{j'},f_y^i))} \tag 7\]
  • $s_{nce}$는 위의 psuedo-code와 동일하다.
  • $s_{nce}(f^j_1, f^i_7)$이 주어지면 이를 이용해 $q$를 정의할 수 있다. 하지만 식 (7)에 나타나듯 $q$는 어떤 negative sample인지에 따라 확률적으로 달라질 수 있으므로, 어떤 negative sample이 와도 어느정도 동일한 결과를 도출 할 수 있도록 entropy term $\alpha H(q)$를 추가한다

4. Experiments

Datasets

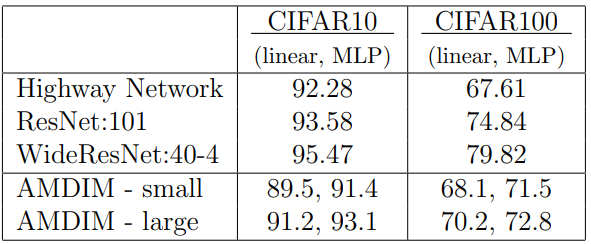
• CIFAR10 : $91.2%$/$93.1%$($\mathrm {Linear}$/$\mathrm{MLP}$)/CIFAR100 : $70.2%$/$72.8%$($\mathrm {Linear}$/$\mathrm{MLP}$)

  • 작은 모델 : $\mathrm{ndf}=128$, $\mathrm{nkrhs}=1024$, $\mathrm{ndepth}=10$

  • 큰 모델 : $\mathrm{ndf}=320$, $\mathrm{nkrhs}=2048$, $\mathrm{ndepth}=10$

    

• STL10 : 각 5000개의 샘플을 가진 10개의 클래스로 구성, $94.2%$/$94.5%$($\mathrm {Linear}$/$\mathrm{MLP}$)

  • 모델 : $\mathrm{ndf}=192$, $\mathrm{nkrhs}=1536$, $\mathrm{ndepth}=8$

• ImageNet : $70.2%$/$72.8%$($\mathrm {Linear}$/$\mathrm{MLP}$)

  • 모델 : $\mathrm{ndf}=320$, $\mathrm{nkrhs}=2536$, $\mathrm{ndepth}=10$

Ablation on STL10 and ImageNet

논문에서 도입한 regularization과 multiscale, data augmentation의 영향을 평가해본다.

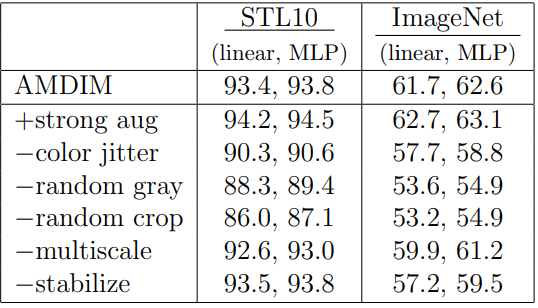
STL10과 ImageNet에서 모두 같은 모델을 사용했고, ImageNet의 경우 위에서 사용한 모델보다 작은 모델을 이용해 성능이 더 낮게 나온다.

Transfer Learning to Places205

Transfer Learning 성능을 평가해본다.

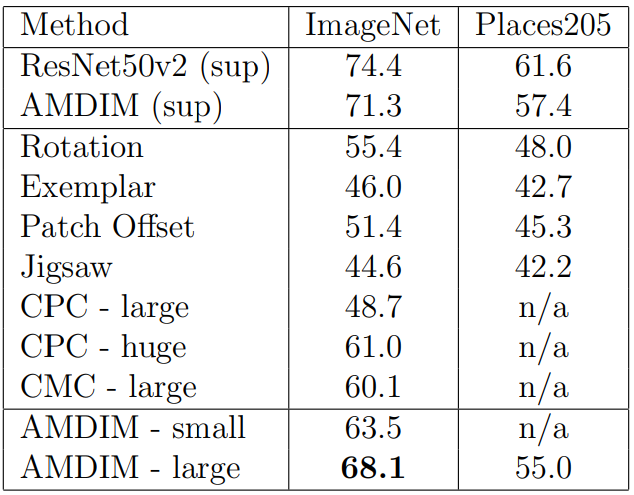
• 작은 모델 : $\mathrm{ndf}=192$, $\mathrm{nkrhs}=1536$, $\mathrm{ndepth}=8$
• 큰 모델 : $\mathrm{ndf}=320$, $\mathrm{nkrhs}=2560$, $\mathrm{ndepth}=10$
• 모두 finetuning 했다.

Visualization

(a)는 ImageNet, (b)는 Places205 데이터셋을 이용해 시각화한 결과이다. 각 열은 제일 왼쪽열을 기준으로 $f_1$의 cosine-similarity가 가장 가까운 7개의 이미지를 나타낸다. 두 번째, 네 번째 행은 matching score $\phi_1(f_1)^\top\phi_7(f_7)$를 나타낸다.

• ImageNet에서 올바른 이미지들은 matching score가 객체에서 높지만, 그렇지 않은 이미지들은 배경에서 높다. 이런 경향은 Places205에서 더욱 심하다.

(c)와 (d)는 $[f_1(x^1), f_7(x^2)]$, $[f_7(x^1),f_7(x^2)]$, $[f_5(x^1), f_5(x^2)]$간의 similarity를 나타낸다.

각각 $f_1$에 $k=2, 3,3,4$인 $m_k$를 적용했을때 $q(f_1^k(x^1)|f_7(x^2))$를 시각화한 것이다. 왼쪽이 $x^1$, 오른쪽이 $x^2$이다.

• Segmentation과 유사한 현상이 나타난다.

5. Discussion

• Shared context를 가지는 multiple views에서 얻어낸 feature들 사이의 mutual information을 최대화하는 self-supervised learning방식을 제안한다.
• 이미지 외에도 비디오나 오디오, 텍스트 등의 다양한 도메인에서 사용 될 수 있다.
• Mixture-based representation과 NCE-based mutual information bound에서 regularization의 역할에 관한 추가적인 연구가 필요하다.