Training Very Deep Networks

관련 링크 : https://arxiv.org/abs/1507.06228

Architecture : HighwayNet(2015)

Abstract

많은 연구들이 인공 신경망의 깊이가 성능을 향상시킴을 밝혀왔지만, 깊은 인공 신경망을 학습시키기는 여전히 어렵다. 본 논문은 정보의 흐름을 조절하는 gating unit을 통해 정보가 특정층을 거치지 않는 highway 구조를 사용하면서 수백층의 깊은 인공 신경망을 학습시켰다.

1. Introduction

이론적인면에서, 깊은 신경망이 얕은 신경망보다 특정 함수들을 더 효율적으로 표현할 수 있음은 잘 알려져있다. 또한 깊은 신경망을 학습시키는건 상당히 어렵다는 것도 증명되었다. initialization schemes(He), multi stage training(VGGnet), 추가적인 loss(Googlenet)의 사용도 더 깊은 층은 학습시킬 수 없었다.

이런 방법들의 일환으로, skip-connection이 사용되어 왔는데, 최근에는 특히 정보의 흐름을 개선하기 위한 목표로 사용되었다.

본 논문은 개요에서 말한것 처럼 어떤 깊이의 신경망도 학습시킬수 있는 구조를 제안한다. 이 구조는 LSTM에서 영감을 받은 gating mechanism을 이용했고, 이 덕분에 정보가 특정층을 통과하지 않고 전달되는 통로(imformation highway)를 가질 수 있었다.

실험을 통해, 일반적인 신경망은 층이 깊어질수록 학습시키기 어려웠던것과 대조적으로 highway 네트워크의 학습은 층수와는 상관없음을 보았다.

2. Highway Netwroks

Notation

• 행렬과 벡터는 굵은 문자로 나타낸다.
• TRANSFORM FUNCTION은 이탤릭체 대문자로 나타낸다.
• zero, one, identity matrix는 각각 $\boldsymbol0$, $\boldsymbol 1$, $\mathbf I$로 나타낸다.
• $\displaystyle \frac 1 {1+e^{-x}}$ 는 $\sigma(x)$로 정의한다.

$\mathbf W_{\mathbf {H, l}}$를 파라미터로 사용하는 non-linear transfrom $H$가 있다. $H$는 입력이 $\mathbf x_{1}$일때 $\mathbf y_1$을 출력한다. 일반적인 network는 각각 $H$인 $L$개의 층을 가지고, 다음과 같이 나타낼 수 있다.

\[\mathbf y = H(\mathbf {x,W_H}) \tag 1\]

간단히 나타내기 위해 layer index와 bias를 생략했다. $H$는 보통 affine-activation으로 쓴다.

하지만 Highway network의 경우 다르게 나타낸다.

\[\mathbf y = H(\mathbf {x, W_H})\cdot T(\mathbf {x, W_T}) + \mathbf x \cdot C(\mathbf {x, W_C}) \tag 2\]

여기서 $T$는 trasnform gate, $C$는 carry gate라고 한다. 논문에서는 $C=1-T$로 정의하고 진행할 것이므로, 식은 아래와 같이 바뀐다.

\[\mathbf y = H(\mathbf {x, W_H})\cdot T(\mathbf {x, W_T}) + \mathbf x \cdot (1-T(\mathbf {x, W_T})) \tag 3\]

따라서 $\mathbf y$과 $\displaystyle {d\mathbf y \over d\mathbf x}$는 아래와 같이 볼 수 있다.

\[\mathbf y = \begin{cases} \mathbf x, &\mbox {if } T(\mathbf{x, W_T})=0\\ H(\mathbf{x, W_H}), &\mbox{if } T(\mathbf{x, W_T})=1 \end{cases} \tag 4\] \[{d\mathbf y \over d\mathbf x} = \begin{cases} \mathbf I, &\mbox {if } T(\mathbf{x, W_T})=0\\ H'(\mathbf{x, W_H}), &\mbox{if } T(\mathbf{x, W_T})=1 \end{cases} \tag 5\]

종합하면 일반적인 network는 $H$만을 계산하지만, highway network는 $H$, $T$ 둘 다 계산해서 다름 층으로 넘긴다.

2.1 Constructing Highway Networks

(3) 식을 보면, 입력과 출력, 그리고 $H(\mathbf{x,W_H})$, $T(\mathbf{x,W_T})$의 차원이 모두 같아야 한다. 하지만 차원 변환이 필요한 경우가 있을수 있다. 그럴때는 두 가지 방법이 있는데, 논문에서는 후자의 방법을 사용했다.

• $\mathbf x$를 sub-sampling하거나 zero-padding한 $\mathbf{\hat x}$를 이용한다.
• 일반적인 레이어를 거친 후 highway 레이어를 쌓는다.

Convolutional highway의 경우도 동일하고, 입려과 출력의 resolution을 맞추기 위해 zero-padding을 사용했다.

2.2 Training Deep Highway Networks

일반적인 네트워크는 He initialization으로 초기 분산을 유지시켜주지 않으면 학습되지 않는다. Highway 네트워크의 경우는 $H$의 기능에 따라 초기화 방식이 다르다.

$T(\mathbf x)=\sigma(\mathbf {W_T ^{\mathcal T} x +b_T} )$라 하자. 이때 $C$가 잘 동작하도록 $\mathbf {b_T}$를 음수로 초기화했다. 실험을 통해, 바이어스 $\mathbf {b_T}$를 음수로 초기화시키기만 해도 다양한 $\mathbf {W_H}$를 평균이 0인 분포로 초기화시킨 깊은 네트워크가 학습이 잘 진행됨을 확인했다.

효율적인 initialization scheme을 찾을 필요가 없으므로 중요한 특징이다.

3. Experiments

모든 네트워크는momentum SGD로 학습되었다. Section 3.1에서는 exponentially decaying learning rate를 이용했고, 나머지는 $\lambda$로 시작해서 학습이 중단될때마다 $\gamma$로 나눠주는 방식을 이용했다. $\lambda, \gamma$는 validation set으로 정했다. $H$에 사용될 활성화 함수는 ReLU를 사용했고, random initialization으로 인한 분류 결과의 변동성을 잘 추정하기위해 결과는 5번 실행한 값을 $Best(mean\pm std.dev)$로 나타냈다.

exponentially decaying : $\alpha = \alpha_0 e^{-kt}$

3.1 Optimization

층수의 영향을 비교하기위해 Xavier/He initialization을 수행한 일반적인 네트워크와 highway 네트워크를 비교한다. 두 네트워크 모두 MNIST dataset을 이용했고 각 층당 거의 유사한 파라미터를 가지도록 highway는 50 blocks, 일반적인 네트워크는 70 units을 가진다. 각 네트워크는 첫번째 층은 무조건 FCL이고, 그 이후 각각 9, 19, 49, 99개의 일반/highway 층을 가진다. 마지막엔 softmax 층을 가진다.

learning rate, momentum, exponential decay factor, 활성화 함수(ReLU or tanh), $\mathbf {b_T}$등의 hyperparameters는 100번의 random search로 찾았다.

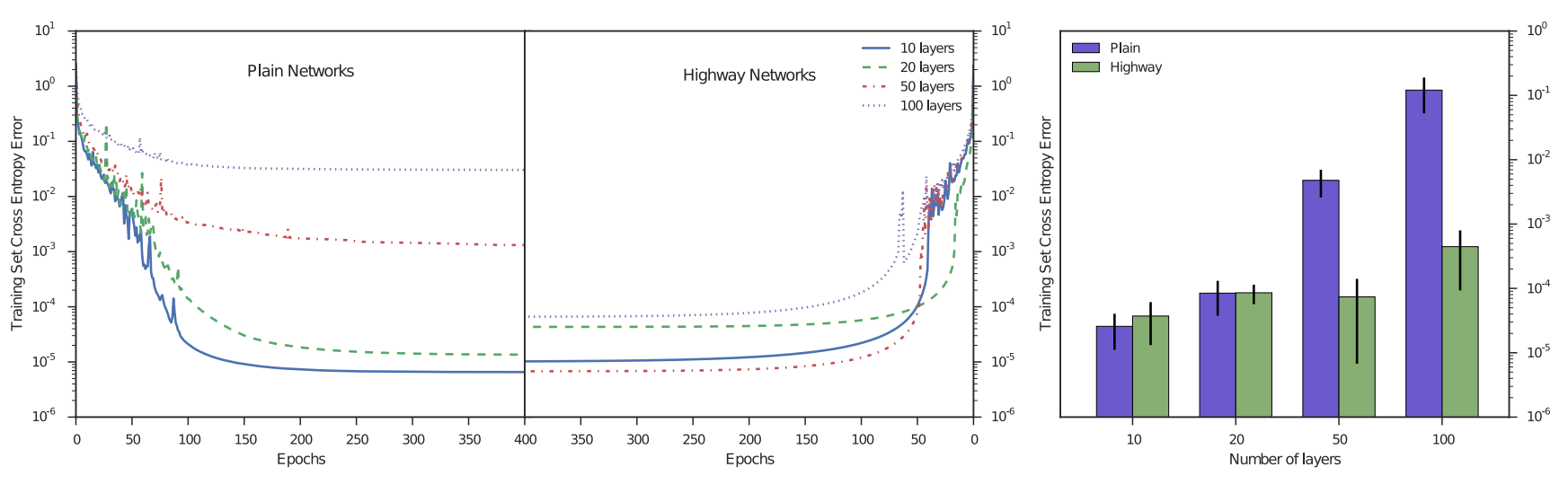
결과는 위의 그림과 같다. 층 깊이가 얕을때는 일반적인 네트워크가 highway와 비슷하지만 깊어질수록 성능이 나빠짐을 볼 수 있다. 또 highway가 더 빨리 수렴하는것도 관찰된다.

3.2 Pilot Experiments on MNIST Digit Classification

Highway의 일반화 능력을 확인하기 위해 9개의 conv 층과 한개의 softmax층을 가진 두개의 네트워크를 학습시켰다. filter maps의 크기는 각각 16, 32로 설정했다.

3.3 Experiments on CIFAR-10 and CIFAR-100 Object Recognition

3.3.1 Comparison to Fitnets

Fitnet training

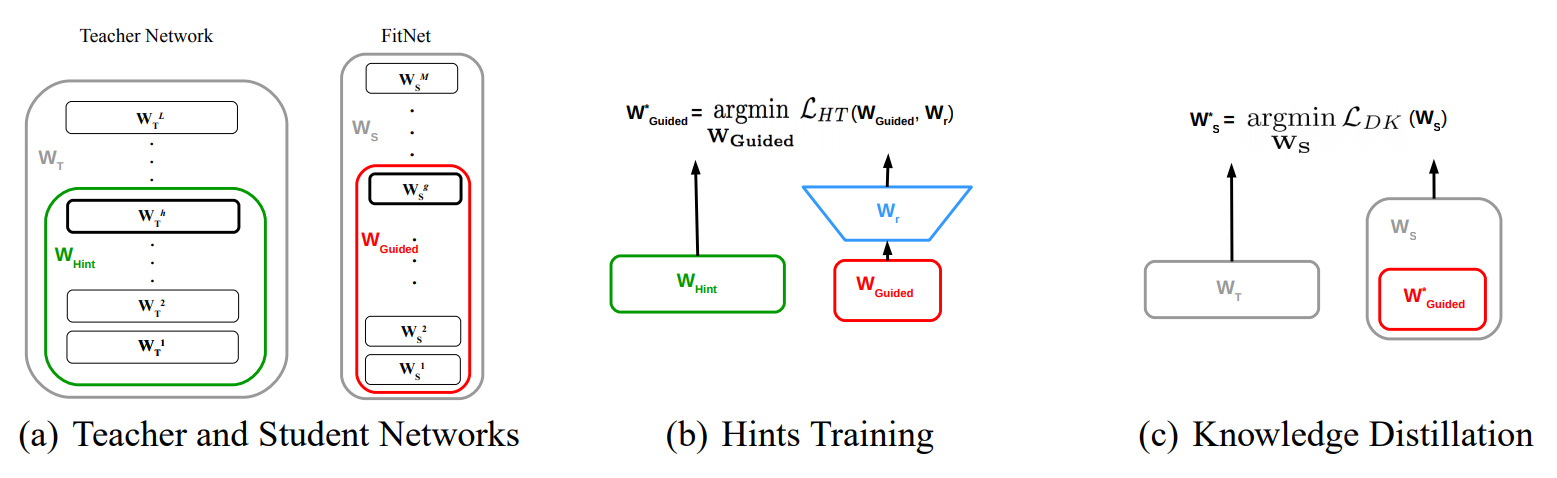
Maxout network는 깊어진 층을 기존 방법보다 잘 학습했지만, 기준 연산량을 벗어나면 학습할 수 없는 한계를 가지고 있었고, 이 한계를 학습 과정을 두 단계로 늘린 hint-based learning으로만 해결할 수 있었다.

하지만 highway network는 거의 비슷한 파라미터를 가진 모델을 한 단계만에 학습했다.

3.3.2 Comparison to State-of-the-art Methods

논문의 목적은 네트워크의 깊이에 따른 학습의 어려움을 해결하는 것이므로, CIFAR-10, CIFAR-100 dataset에 Global Contrast Normalization, small translation, mirroring만 수행했다. Network-In-Network 논문에 따라, FCL를 convolutional layer로 대체하고 global average pooling layer를 사용했다. hyperparameters는 MNIST model의 것을 그대로 사용했다.

Global Contrast Normalization/feature-wise : 전체 이미지에 대해서 전체 픽셀들의 분포가 평균이 0이고 분산이 1인 정규분포로 만드는 것, 대조적으로 각 이미지에대해 표준화하는 sample-wise/Local Contrast Normalization이 있다.

Translation : 이미지를 몇 픽셀씩 밀어버리는 것. 빈 공간은 0으로(zero filling) 채우거나, 가까운 픽셀로(nearest neighbor) 채우거나, 밀린 부분을 가져와서(rolling) 채운다.

4. Analysis

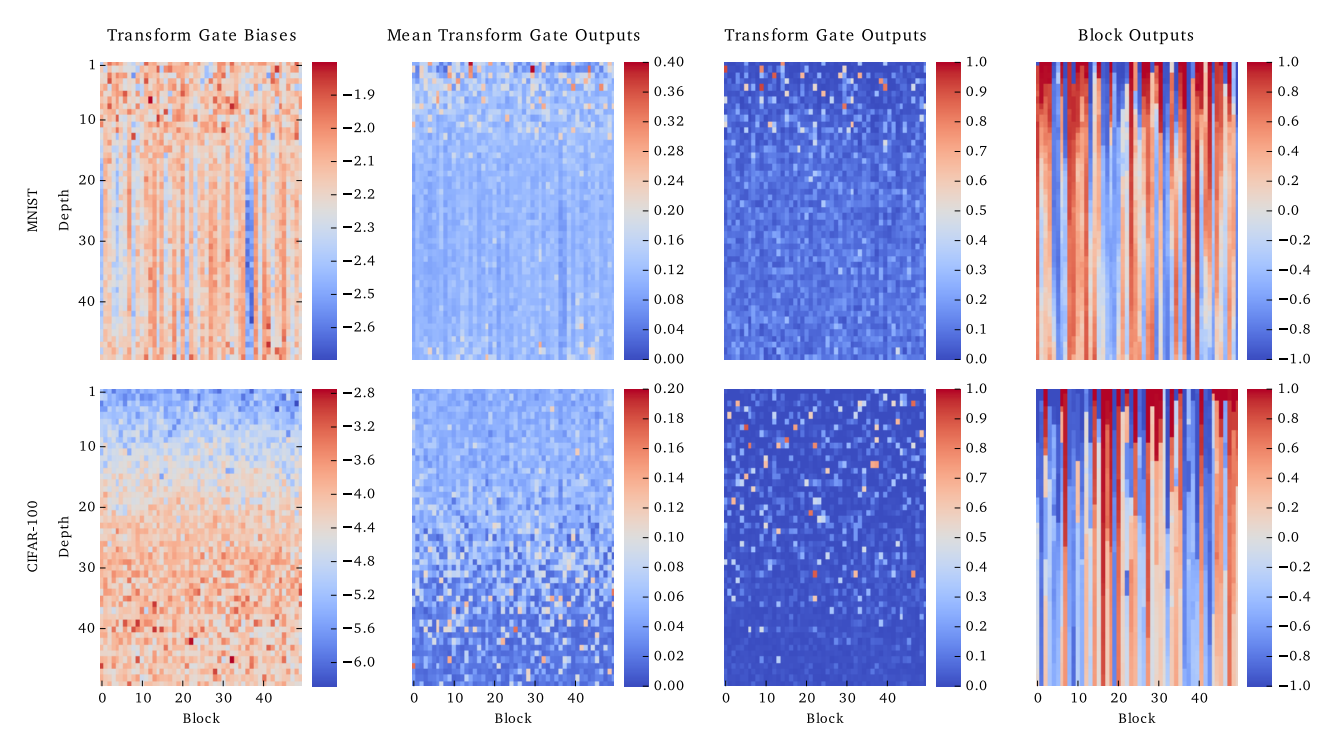
각 행은 MNIST, CIFAR-100, 각 열은 $\mathbf{b_T}$, $mean(T(\mathbf{x_{all}, W_T}))$, $T(\mathbf{x_{random}, W_T})$, $Block(\mathbf{x_{random}})$을 뜻한다. 학습시 $\mathbf {b_T}$는 각각 -2, -4로 초기화했다. 첫번째 층은 차원을 맞추기 위한 일반적인 층이고, 나머지 49개층은 50 block을 가진 highway층이다. 각 층은 $tanh$를 활성화 함수로 사용한다.

$\mathbf {b_T}$가 학습되면서 증가할 것이라는 기대와 달리 증가했고 이는 $mean(T(\mathbf{x_{all}, W_T}))$가 감소한 것과는 반비례한다. 이는 낮은 층에서 $T$를 닫기위해 강한 $\mathbf {b_T}$를 사용한 의도와는 달리 $T$가 더욱 선택적으로 작용하게 만들었음을 뜻한다. 이는 $T(\mathbf{x_{random}, W_T})$가 더 sparse해짐을 보면 명백해진다. 최종적으로 마지막열을 보면, 특정층 이후로 block의 출력이 동일해지는 ‘information highway’가 잘 시각화되었다.

4.1 Routing of Information

highway는 네트워크가 현재 입력에 따라 유동적으로 shortcut의 연결량을 조정한다. 하지만, 입력에따라 다른 shortcut이 활성화(dynamic routing) 되는건지, 아니면 같은 shortcut만 활성화(static routing)시키는 것인지는 알 수 없다.

Routing이란 패킷이 목적지에 도달할 최적의 경로를 찾아 전송하는 것을 뜻한다. static routing은 경로를 직접 지정하는 것이고, dynamic routing은 망이 직접 변화에 따라 경로를 지정하는 것이다.

이는 CIFAR-100의 두번째와 세번째 열을 비교해서 확인 할 수 있다. 두번째 열은 block들이 평균적인 값을 가지는 반면, 세번째 열은 특정 block만 활성화 되어있다. 이는 각 sample에서 다른 block들이 활성화됨을 의미한다. 추가적인 근거는 다른 class에 따라 $mean(T(\mathbf{x_{all}, W_T}))$을 나타낸 결과에서도 확인할 수 있다.

MNIST는 15층 전, CIFAR-100은 전층에서 class에 따라 다른 block이 활성화 됨을 볼 수 있다.

4.2 Layer Importance

초기에 $\mathbf {b_T}$를 음수로 줘서 $T$가 닫힌것 처럼 동작하도록 했는데, 실제로 이 과정이 학습에 도움이 되는지를 확인하기 위해 특정층은 수동으로 $T$를 닫고 실험을 했다.

특정 층 하나의 $T$를 완전히 닫았을때 최종 정확도에 미치는 영향은 위와 같다. 점선은 어떤 층도 닫지 않았을때의 성능이다.

MNIST를 보면 15층까지는 최종성능에 영향을 주지만, 그 외의 층은 거의 영향이 없다. 대조적으로 CIFAR-100의 경우는 대부분의 층이 최정성능에 영향을 준다. 이는 MNIST 같은 깊은 층이 필요없는 문제는 대부분의 층이 의미있는 feature를 학습하지 못하고 불필요한 통로의 역할만 수행하지만, CIFAR-100 같은 복잡한 문제는 대부분의 층이 어느정도 의미있는 feature를 학습함을 뜻한다.

5. Discussion

앞서 여러 연구들이 initialization methods나 복잡한 convolutional/recurrent layer를 이용해서 깊은 네트워크들을 학습시켰다면, highway 네트워크는 gating mechanism을 이용해 특정 정보를 전달해서 약간의 파라미터만 추가해 깊은 네트워크를 학습시킬수 있었다.

이 과정에서, 많은 층들이 불필요하게 존재함을 확인했고, 해결하고자 하는 문제에 적합한 층의 깊이를 얻는 방법도 알게 되었다.