Self-Supervised Learning of Pretext-Invariant Representations

관련 링크 : https://arxiv.org/abs/1912.01991

Self-Supervised Learning : PIRL(2019)

Abstract

Self-supervised learning의 목표는 semantic annontation을 필요로하지 않는 pretext를 통해 의미있는 image representation을 만드는 것이다. 많은 pretext task가 image transformation과 covariant하지만, 본 논문은 semantic representation이 trasnformation에 invariant하다고 생각하고, Pretext-Invariant Representation Learning(PIRL)을 제안한다. 본 논문은 Jigsaw puzzle을 해결하는 PIRL을 사용하고 supervised-pretraining 이상의 성능을 보였다.

1. Introduction

현실 세계의 이미지에는 수 많은 카테고리가 있지만 학습에 사용되는 카테고리는 가장 빈도가 높은 카테고리들 뿐이다. 따라서, 사람이 사전 정의한 라벨을 이용한 학습은 ‘long tail’에서는 좋은 성능을 보이지 못하고 이는 Image recognition의 발전을 막는다. 하지만, Self-supervised learning은 사전 정의한 주석과 무관하게 이미지의 pixel 그 자체로 representation을 학습하므로 이 문제를 해결한다.

• Long Tail은 아래 그림의 노란색 부분을 말한다. Y축은 발생 빈도이다.

Self-supervised learning은 주로 이미지에 변환을 주고, 그 변환을 예측하도록 pretext task를 구성하는 것으로 이루어지고, 모델은 변환과 covariant한 representation를 학습한다. 하지만 이미지 변환이 visual semantic을 바꾸지는 않으므로, 실제로 recognition에 유용한 것은 이미지 변환에 invariant representation이다.

본 논문은 이를 이용한 Pretext-Invariant Representation Learning(PIRL)를 제안한다. PIRL은 변환된 이미지와 유사하고 변환되기 전 이미지와는 다른 representation을 구축한다. 변환 방법은 Jigsaw를 사용한다.

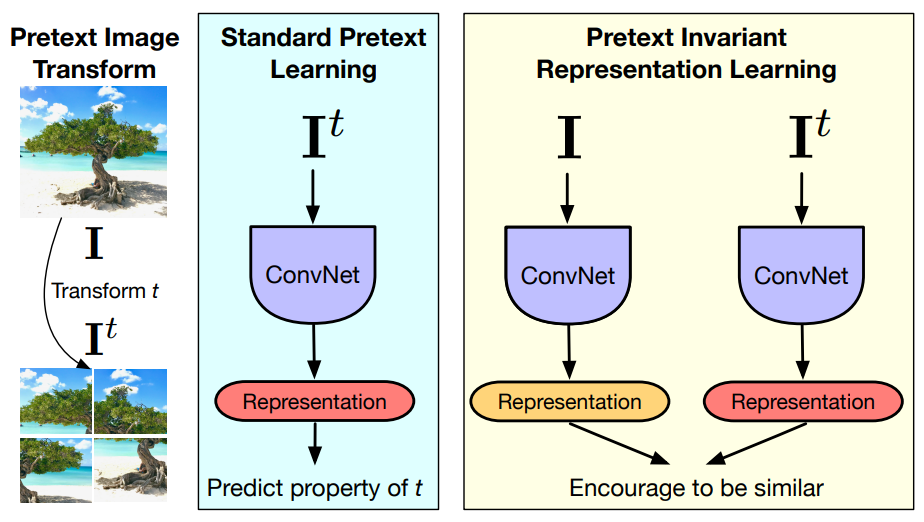
여러 실험을 수행한 결과, PIRL 기존의 다른 방법들보다 좋은 성능을 보였고 Obejct Detection에서는 supervised보다도 뛰어난 성능을 보였다.

2. PIRL: Pretext-Invariant Representation Learning

기존 연구들이 사용하는 pretext task는 다양하고, 이는 모두 covariant representation을 학습시킨다. 하지만 본 논문은 기존의 pretext task로 invariant representation을 학습하는 방법을 제안한다. 이를 증명하기위해 Jigsaw pretext task를 가지고 실험을 진행하고, 다른 pretext task에서도 효과가 있음을 보여 줄 것이다.

2.1 Overview of the Approach

주어진 데이터셋을 $\mathcal D = \{\mathbf I_1, \ldots , \mathbf I_{|\mathcal D |}\}$($\mathbf I_n \in \mathbb R ^{H \times W \times 3} $), 이미지 패치를 뒤섞거나(Jigsaw), 회전시키는 변환들을 $\mathcal T$라고 하자. 우리는 이미지 변환 $t \in \mathcal T$에 invariant한 representation $\mathbf {v_I} = \phi_\theta(\mathbf I)$를 만드는 파라미터 $\theta$를 가지는 네트워크 $\phi_\theta(\cdot)$를 학습시키는게 목표다. 논문에서는 이를위해 empirical risk minimization을 이용한다.

• Empirical risk minimization : Training set에서 loss를 최소화하는 함수, $min(error_{train})$

• Structural risk minimization : Training set에서 loss를 최소화하면서 training set에 정규화를 적용하는 함수, $min(error_{train}+complexity(Model))$

위 개념에 대한 자세한 설명 : 관련 글

수식으로 나타내면 아래와 같다. (1)은 논문의 방식, (2)는 기존 연구들의 방식이다. (1)은 원본 이미지, 변환된 이미지 모두에서 뽑은 representation을 이용해 invariant representation을 학습하지만 (2)는 원본 이미지와 변환의 성질을 이용하기 때문에 covariant representation을 학습한다.

\[\ell _{inv}(\theta ;\mathcal D)=\mathbb E _{t\sim p(\mathcal T)}\left [\frac {1}{|\mathcal D|} \sum _{\mathbf I \in \mathcal D}L(\mathbf{v_I}, \mathbf v_{\mathbf I^t})\right ] \tag 1\] \[\ell _{co}(\theta ;\mathcal D)=\mathbb E _{t\sim p(\mathcal T)}\left [\frac {1}{|\mathcal D|} \sum _{\mathbf I \in \mathcal D}L_{co}(\mathbf{v_I}, z(t))\right ] \tag 2\]

• $p(\mathcal T)$ : $\mathcal T$의 분포
• $\mathbf I^t$ : $t$가 적용된 후의 이미지 $\mathbf I$
• $L(\cdot, \cdot)$ : 두개의 representation 사이의 유사성을 측정하는 loss function
• $L_{co}$ : 기존 방식이 사용하는 loss function
• $z(t)$ : 이미지 변환 $t$의 특징을 측정하는 함수

Loss function

논문에서 사용하는 loss function은 Noise contrastive estimator를 이용한다. Positive sample을 $(\mathbf I,\mathbf I^t)$의 feature, Negative sample은 $\mathbf {I’}\not= \mathbf I$인 $N$개 image의 feature라고 할때, NCE는 다음과 같이 표현된다.

Noise contrastive estimator : 일반적으로 출력이 많은 classifier를 훈련시키는데 사용된다. 많은 출력에 Softmax를 계산하는 것은 연산량이 많으므로, 실제분포와 인위적으로 생성된 noise 분포를 구분하도록 학습시켜 문제를 binary classification으로 줄일 수 있다.

자세한 설명, 추후 이걸 기반으로 정리할 것

\[h(\mathbf {v_I}, \mathbf v_{\mathbf I^t}) = \frac {\mathrm {exp}\left(\frac {s(\mathbf {v_I}, \mathbf v_{\mathbf I^t})}{\tau}\right)}{\mathrm {exp}\left(\frac {s(\mathbf {v_I}, \mathbf v_{\mathbf I^t})}{\tau}\right)+\sum_{\mathbf I' \in \mathcal D_N}\mathrm {exp}\left(\frac {s(\mathbf {v_{I'}}, \mathbf v_{\mathbf I'})}{\tau}\right)} \tag 3\]

• $\mathcal D_N \subseteq \mathcal D\backslash {\mathbf I}$ : 이미지 $\mathbf I$를 제외한 $\mathcal D$에서 무작위로 가져온 $N$개의 negative sample set

• $s(\cdot, \cdot)$ : 두 representation 사이의 cosine similarity score

• $\tau$ : temperature parameter

  Cosine similarity :

  • ${\displaystyle {\text{similarity}}=\cos(\theta )={A\cdot B \over \|A\|\|B\|}={\frac {\sum \limits _{i=1}^nA_i\times B_i}{\sqrt{\sum \limits _{i=1}^n(A_i)^2}\times \sqrt {\sum \limits _{i=1}^n(B_i)^2}}}}$

실제로 $s(\cdot, \cdot)$를 계산하기전에 $\mathbf v$를 다양한 ‘head’에 적용시킨다. 구체적으로, $\mathbf {v_I}$에는 $f(\cdot)$, $\mathbf v_{\mathbf I^t}$에는 $g(\cdot)$을 적용한다. 따라서 loss function는 다음과 같다.

\[L_\mathrm {NCE}(\mathbf I,\mathbf I^t) = -\mathrm {log}[h(f(\mathbf {v_I}),g(\mathbf v_{\mathbf I^t}))]- \sum_{\mathbf I' \in \mathcal D_N} \mathrm log[1-h(f(\mathbf v_{\mathbf I'}),g(\mathbf v_{\mathbf I^t}))] \tag 4\]

이 loss function은 $\mathbf v_{\mathbf I^t}$와 $\mathbf v_\mathbf I$는 같게, $\mathbf v_{\mathbf I’}$와 $\mathbf {v_I}$는 다르게 만들어 준다.

2.2 Using a Memory Bank of Negative Samples

NCE loss는 negative sample의 수가 많을수록 좋다. 하지만 mini-batch SGD에서 batch size는 제약이 있으므로, batch size를 늘리지않고 negative sample의 수를 늘리기 위해 memory bank $\mathcal M$을 사용한다. $\mathcal M$은 $\mathcal D$의 각 이미지 $\mathbf I$에 관한 representation $\mathbf {m_I}$의 집합이고, $\mathbf {m_I}$는 이전 epoch에서 계산된 $f(\mathbf {v_I})$의 지수이동평균으로 계산된다. 논문에서는 $\mathcal M$을 이용하여 $f(\mathbf v_{\mathbf I’})$를 계산없이 사용한다. $\mathbf {m}_{\mathbf I’}$는 없음을 주의해야 한다.

지수이동평균 : 일반적인 평균에 시간개념을 도입한 평균의 한 종류로, 최신값에 가중치를 두어 평균을 계산한다. 위의 경우에는 epoch이 $k$이고, $f(\mathbf {v_I})$가 $p$라고 볼 수 있다.

\(x_k = \alpha p_k + (1-\alpha)x_{k-1}\)

• $x$ : 지수이동평균값, $p$ : 평균낼 값, $k$ : 시간 인덱스, $\alpha$ : 가중치

Final loss function

$\mathcal M$을 이용하므로 loss fucntion도 달라진다. 최종적인 loss function은 다음과 같다.

\[L(\mathbf I,\mathbf I^t) = \lambda L_\mathrm{NCE}(\mathbf {m_I}, g(\mathbf v_{\mathbf I^t})) + (1-\lambda) L_\mathrm{NCE}(\mathbf {m_I}, f(\mathbf {v_I})) \tag 5\]

위 식의 첫번째 항은 식 (4)와 동일한 역할이고, 두번째 항은 두가지의 역할을 수행한다.

1. $f(\mathbf {v_I})$와 $\mathbf {m_I}$를 유사하게 만들어 파라미터 업데이트의 속도를 줄임

   이 항이 없다면 $\mathbf {m_I}$이 급격하게 변해도 $L$에 크게 반영되지 않는다. 하지만 이 항이 있어서 $\mathbf {m_I}$이 급격히 변하면 $L$가 커지고 optimizer는 이를 줄이기위해 $\mathbf {m_I}$의 변화를 막으므로 업데이트 속도가 줄어든다.

2. $f(\mathbf {v_I})$와 $f(\mathbf v_{\mathbf I’})$를 다르게 만든다.

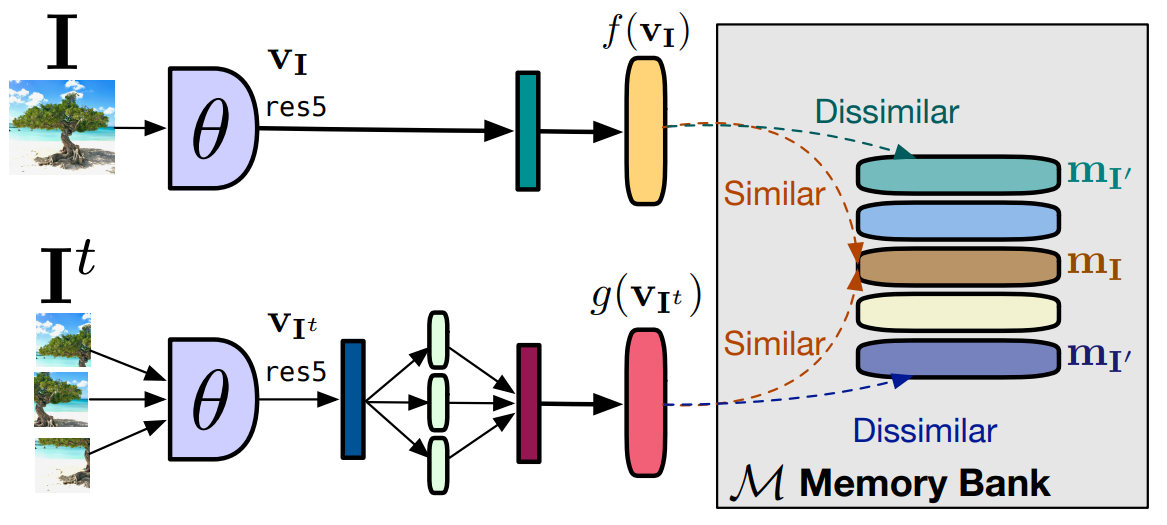
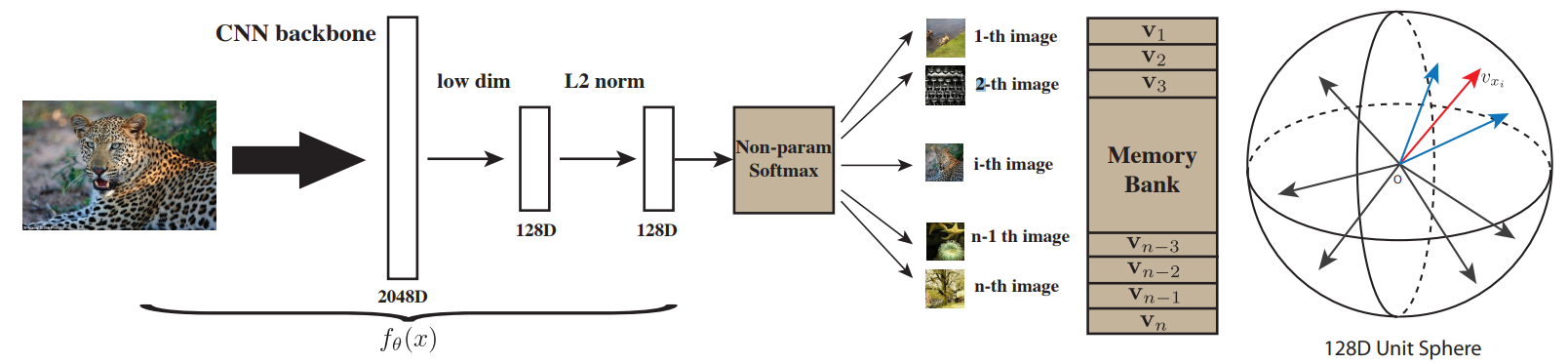
PIRL의 과정을 요약한 그림, 계산된 $\mathrm {v_I}$가 Memory Bank안의 $\mathrm {m_I}$와는 같게, $\mathrm {m_{I’}}$와는 다르도록 학습시킨다.

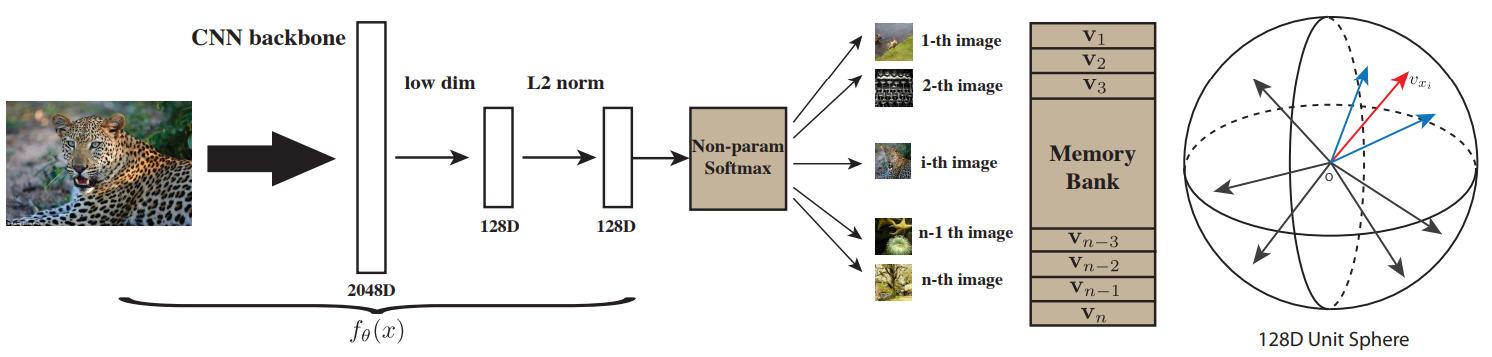
• 아래는 논문에서 자주 언급하는 방법인 NPID로, 각 이미지를 하나의 클래스로 생각하고 각 이미지들이 다른 클래스이므로 representation space에서 최대한 떨어져 있도록 학습시키는 방법이다. non-param softmax를 쓴 이유는 param softmax를 사용하면 이미지가 무엇이든 param에 의해 representation space에서의 초기 위치가 어느정도 결정되기 때문이다.

2.3 Implementation Details

위에서도 언급했듯이 우선 Jigsaw pretext task에서 PIRL을 검증한다. 이에 사용된 세부사항들은 다음과 같다.

Convolutional network

• Image representation을 계산하기위해 ResNet-50를 사용
• $f(\mathrm{v_I})$은 $\mathsf {res5-avgpool-linear}$를 통해 128-dimensional representation을 얻는다.
• $g(\mathrm v_{\mathrm I^t})$은
  1. $\mathbf I$에서 9개의 패치를 뽑는다.
  2. $\mathsf {res5-avgpool-linear}$를 통해 9개의 128-dimensional representation을 얻는다.
  3. 위에서 얻은 9개의 representation을 무작위 순서로 concat 후 다시 $\mathsf {linear}$를 거쳐 최종적인 128-dimensional representation을 얻는다.

Hyperparameters

• 식 (3)의 $\tau=0.07$
• 지수이동평균의 가중치 $\alpha=0.5$
• 식 (5)의 $\lambda=0.5$

3. Experiments

다양한 데이터셋에서 Transfer learning 실험을 통한 PIRL의 성능을 평가한다. object detection과 image classification 성능에 초점을 맞추고 아래의 두가지 세팅으로 실험을 진행한다.

• Transfer learning에서 finetuned를 통한 self-supervised learning의 network initialization 성능 평가
• Trasnfer learning에서 weight fixed를 통한 feature extractor 성능 평가

Baselines

주목해야할 기준점은 Jigsaw ResNet-50과 NPID++이다. 전자는 covariant representation의 성능을 나타내고, 후자는 $\lambda=0$인 식 (5)와 동일하므로 PIRL의 효과를 나타낸다.

NPID++는 기존 NPID방식에서 negative sample의 수와 training epoch를 늘려 성능을 높인 방식이다.

Pre-training data

• 1.28M의 라벨없는 ImageNet 데이터셋

Training details

• RotNet 모델은 Network-In-Network 구조를 이용한다.

• Optimizer는 mini-batch SGD를 사용한다.

  • batch size : $1,024$, total epoch : $800$, number of negative sample $N$ : $32,000$

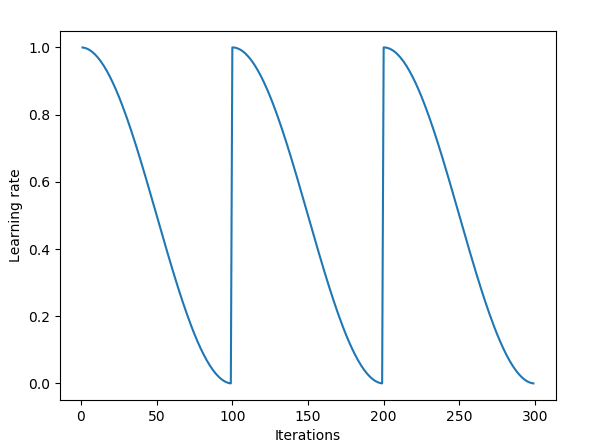
  • lr은 최고 $1.2 \times 10^{-1}$, 최저 $1.2 \times 10^{-4}$인 cosine learning rate decay scheme를 이용한다.

    SGDR: Stochastic Gradient Descent with Warm Restarts에서 사용된 방법이다.

    

  • data-augmentation은 supervised-learning이므로 사용하지 않는다.

Transfer learning

공정한 비교를 위해서 모든 pretext task가 가장 좋은 성능을 내는 hyperparameter를 이용한다.

이와 관련된 세팅은 Scaling and Benchmarking Self-Supervised Visual Representation Learning를 따른다.

3.1 Object Detection

Pascal VOC 데이터셋에서 ResNet-50을 이용한 Faster R-CNN c4를 이용해 object detection을 수행한다. 이때 사용하는 CNN 모델은 ImageNet으로 pretrain한 ResNet-50을 VOC training data로 finetuning한다. (이때 BatchNorm의 파라미터는 fixed한다.) Object detection 성능은 $\mathrm {AP^{all}}$, $\mathrm {AP^{50}}$, $\mathrm {AP^{75}}$로 평가한다.

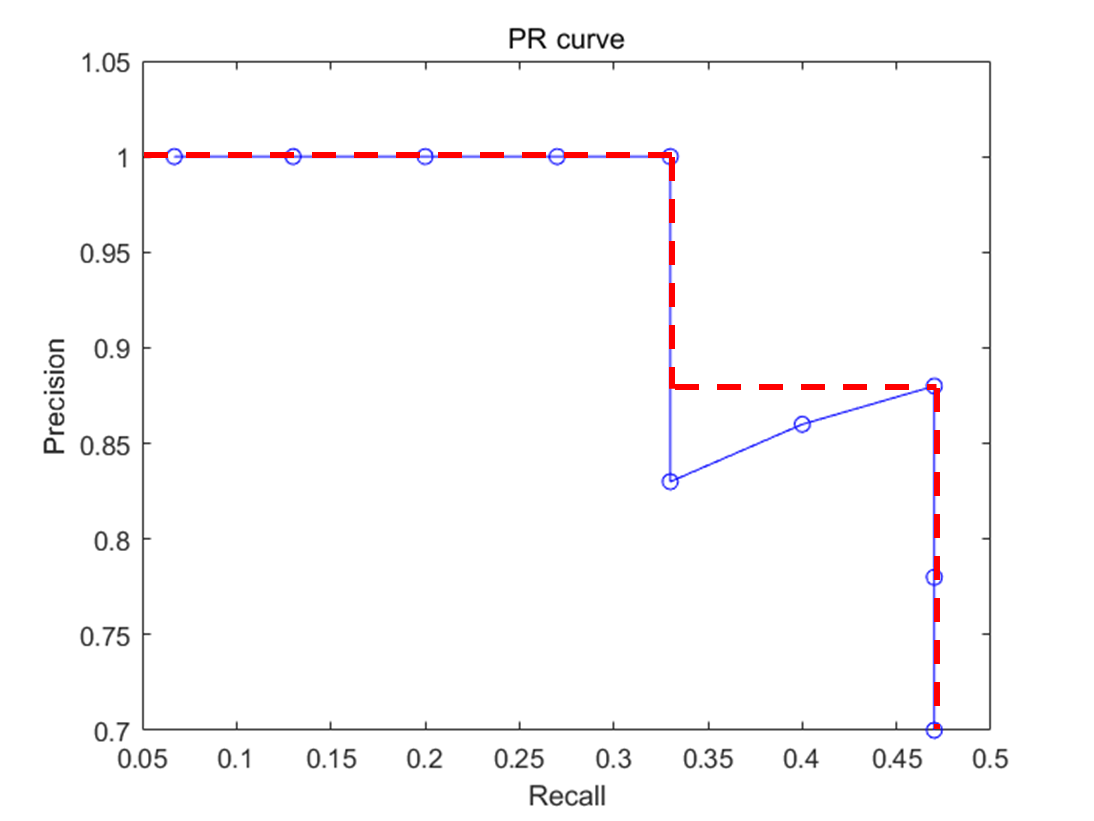
Average Precision : 아래 PR 곡선에서 빨간 점선의 면적을 의미한다. $\mathrm{AP}$에 적혀있는 숫자는 Object Detection에서 True와 False를 결정하는 IoU(Intersection of Union)의 값을 의미한다. $\mathrm {AP^{50}}$ 의 경우 IoU가 50%이상일때 True라고 정했을때 PR 곡선의 면적을 뜻한다.

Test set은 VOC07 test set을 사용했고, 실험 결과는 다음과 같다.

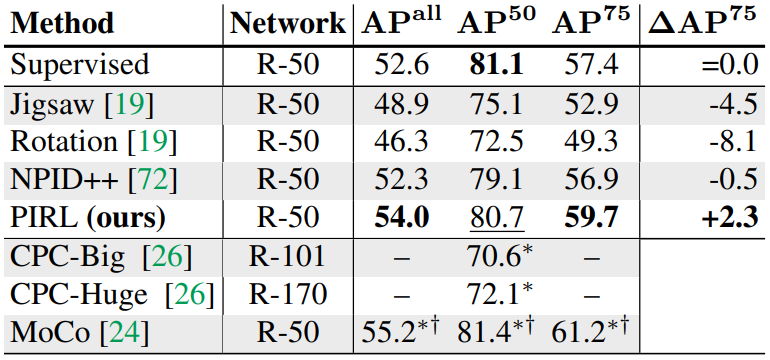
$\dagger$표시는 BatchNorm까지 finetuning한 방법이다. 위는 VOC07+12 training set으로 finetuning시킨 결과인데, 이보다 더 작은 VOC07 train+val set으로 finetuning했을때도 Supervised보다 효과가 좋았다.

3.2 Image Classification with Linear Models

위 실험에서 finetuning으로 initialization 성능을 평가했다면, 이번에는 fixed시켜서 extractor 성능을 평가한다. ImageNet, VOC07, Places205, iNaturalist2018 데이터셋에서 실험을 진행하고, 다른 연구에서처럼 모든 중간층의 representation을 측정한다.

ImageNet results

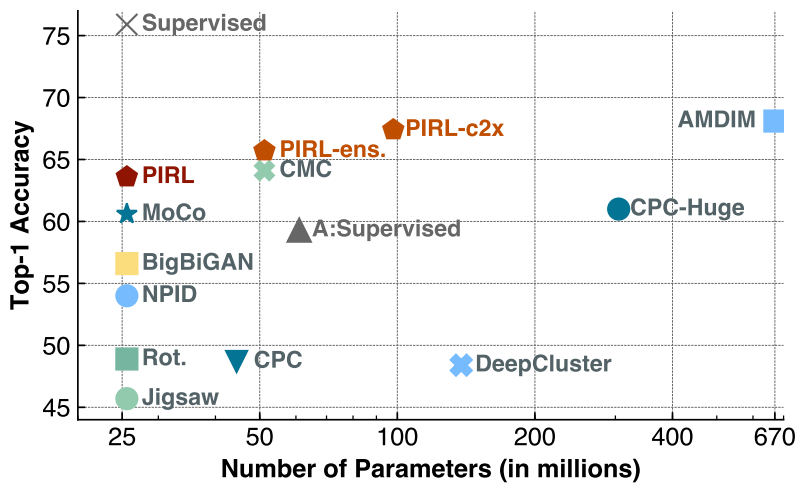
• A는 AlexNet, $\times$는 ResNet-50을 뜻한다.

• PIRl-ens는 Contrastive Multiview Coding를 이용, PIRL-c2x는채널수를 두배로 늘림

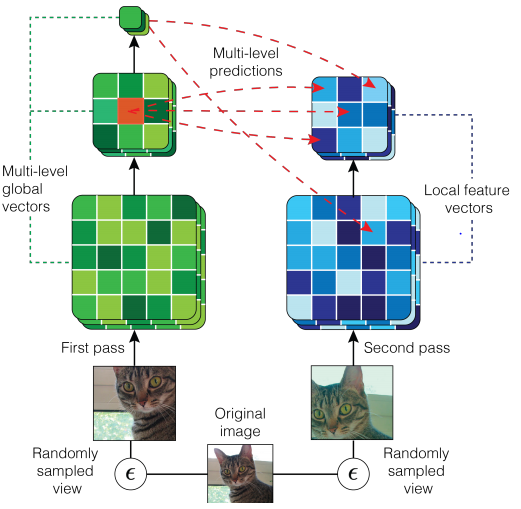
  • Contrastive Multiview Coding : 두개의 ResNet 모델을 이용해서 이미지끼리 비교하지 않고 representation끼리 비교해 loss를 계산하는 방식

  Contrastive learning	Multiview
  	!

Results on other datasets

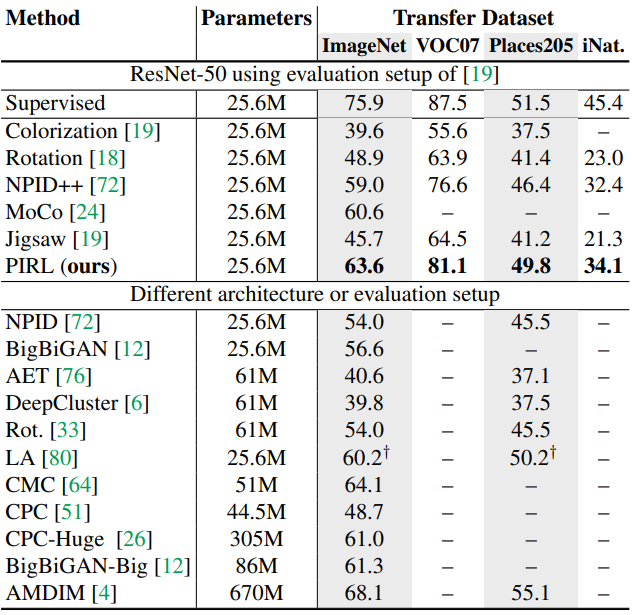
3.3 Semi-Supervised Image Classification

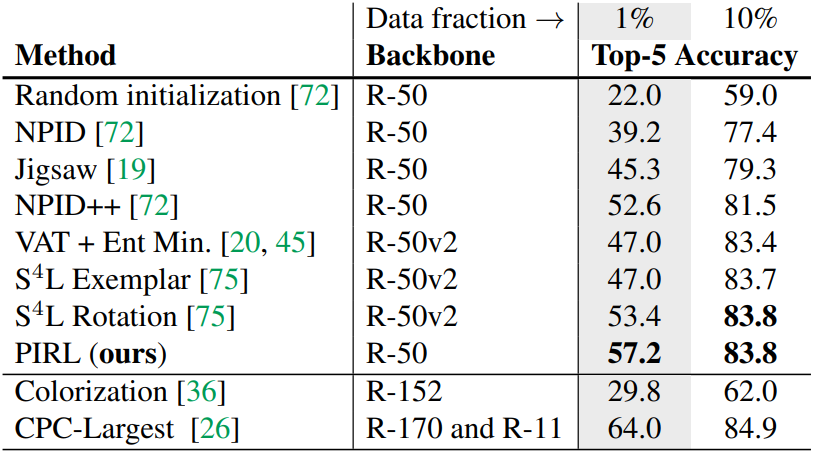
ImageNet training set의 1%, 10%만으로 classifier를 학습시키고 ImageNet validation set으로 test한 결과이다. ${S^4L}$과 ${VAT}$이 semi-supervised learning에 특화된 모델임에도 불구하고 ${PIRL}$보다 못하거나 같은 성능을 보인다.

3.4 Pre-Training on Uncurated Image Data

Pre-training동안 사용된 데이터 분포의 변화가 PIRL에 미치는 영향을 연구하기위해 unlabeled YFCC 데이터셋에서 1M개를 무작위로 뽑은 YFCC-1M으로 모델을 pre-training 한다. Representation의 성능을 평가하는 것이므로 3.2와 동일하게 파라미터를 fixed하고 classifier를 학습시킨다.

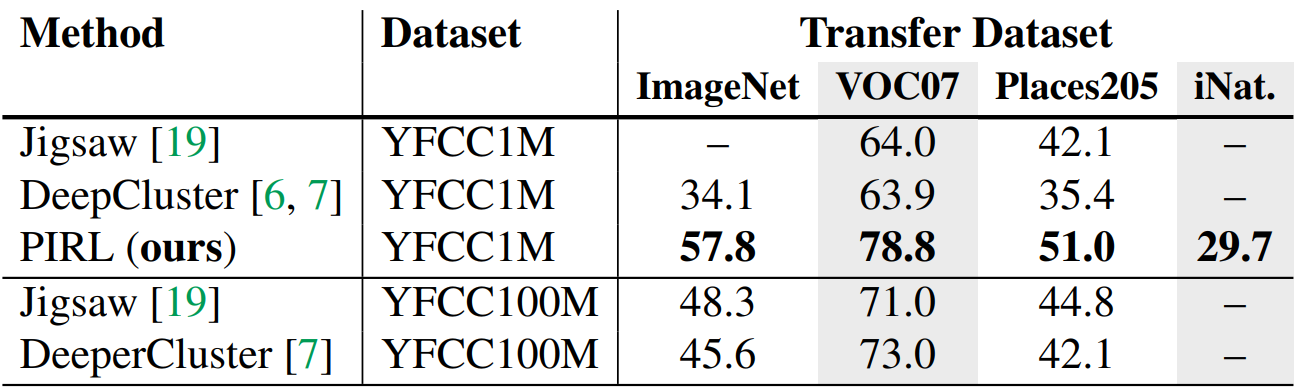
YFCC100M은 100M개의 이미지로 이루어진 데이터셋이다. 이전 결과와 비교했을때, Places205에서는 ImageNet보다 성능이 좋다.

4. Analysis

PIRL의 더 나은 분석을 위해서 많은 모델을 학습시켜야 하므로, 모든 과정은 3.2와 동일하게 진행하되 epoch와 negative sample수를 줄여서 실험한다.

• total epoch : $400$, number of negative sample $N$ : $4,096$(3.2에서는 각각 $800/32,000$)

4.1 Analyzing PIRL Representations

Does PIRL learn invariant representations?

의도한대로 PIRL가 실제로 invariant representation을 학습하는지 검증하기위해 normalized $f(\mathbf {v_I})$와 normalized $g(\mathbf v_{\mathbf I^t})$사이의 $l_2$ distance를 계산한다.

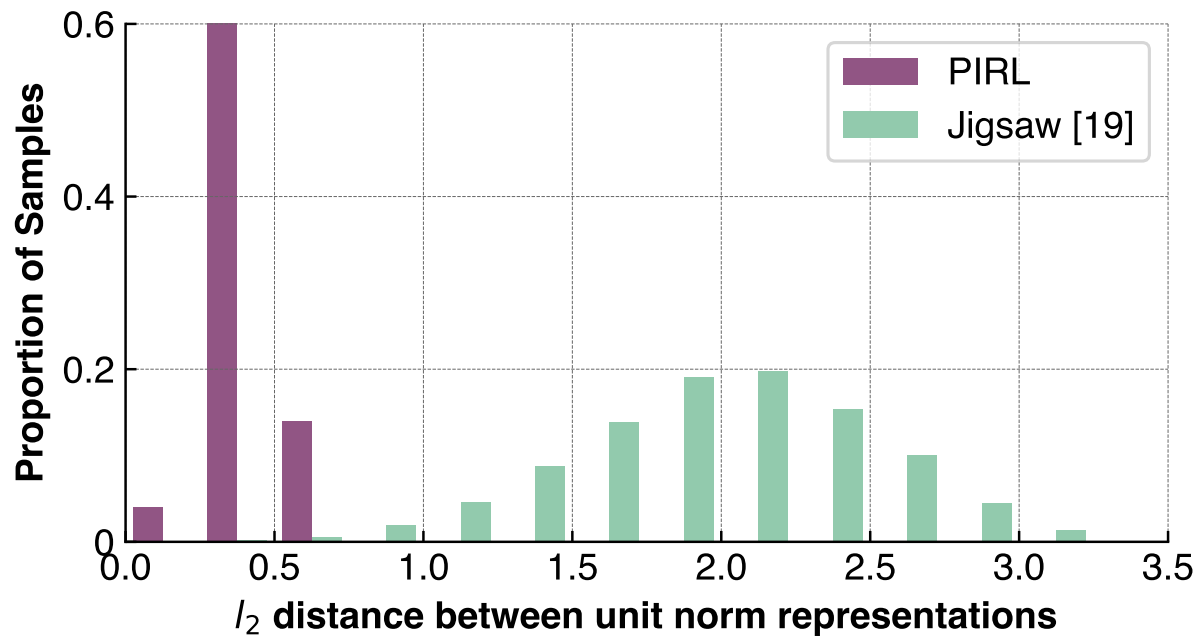
위 그림은 $l_2$ distance의 분포이다. PIRL의 경우 원본 이미지의 representation과 변환 이미지의 representation이 상당히 유사하지만 Jigsaw는 그렇지 않음을 볼 수 있다.

Which layer produces the best representations?

이전 실험에서 PIRL은 $\mathsf {res5}$에서, Jigsaw는 $\mathsf {res4}$의 representation을 이용했다. 이는 Jigsaw의 경우 $\mathsf {res5}$에서는 semantic information보다 이미지 변환과 연관성이 높기 때문이고, 따라서 $\mathsf {res5}$의 representation을 사용할 경우 성능이 급격히 저하된다. 하지만 아래 그림처럼 PIRL은 invariant representation을 학습하도록 설계되었으므로 $\mathsf{res5}$의 representation이 가장 성능이 좋다.

4.2 Analyzing the PIRL Loss Function

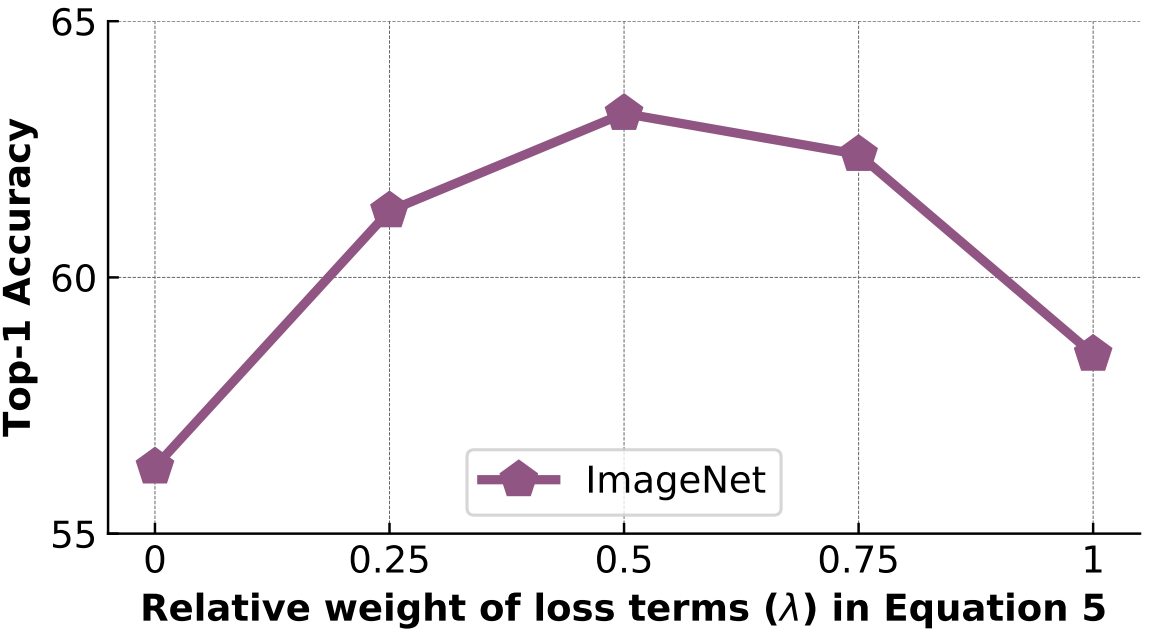
What is the effect of $\lambda$ in the PIRL loss function?

이전 실험에서 식 (5)의 $\lambda=0.5$를 사용했고, NPID는 $\lambda=0$인 경우이다. $\lambda=1$이라면 학습동안 $\mathbf I$와는 비교하지 않고, $\mathbf {m_I}$의 업데이트 속도는 감쇠되지 않을 것이다. 이와같이 $\lambda$가 학습에 미치는 영향이 크기때문에 다른 $\lambda$에서 모델의 성능을 확인한다.

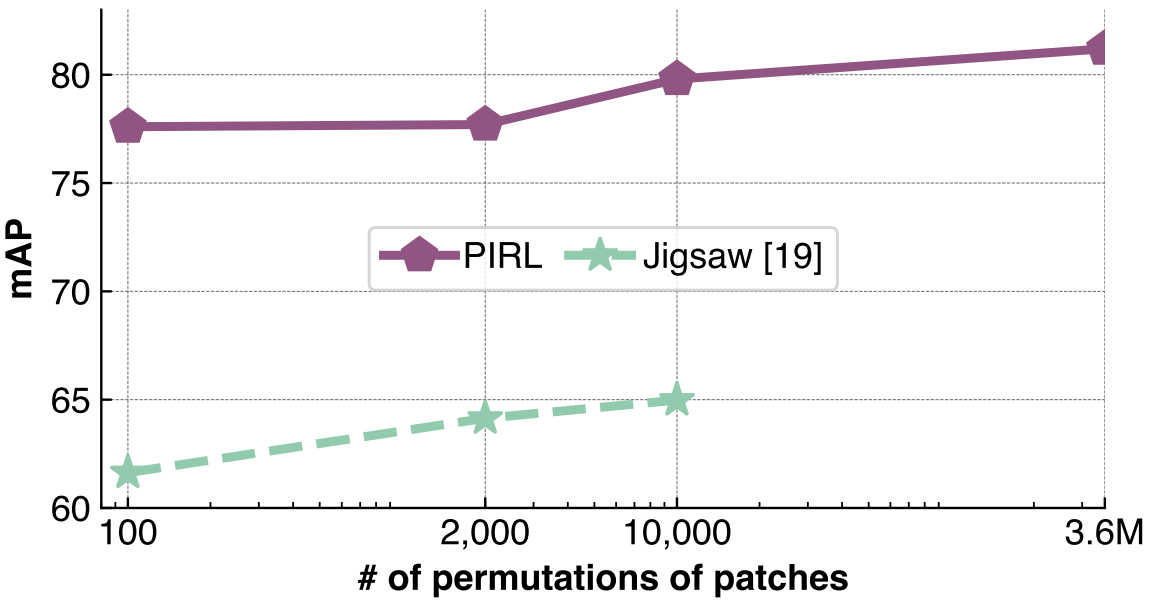
What is the effect of the number of image transforms?

Jigsaw의 경우 패치 조합의 수가 많을수록 성능이 좋아진다. 하지만 이미지에 적용된 패치 조합을 예측하기 위해 출력으로 각 변환별 확률을 만들기 때문에 패치 조합의 수가 증가할수록 파라미터수가 증가해 수가 제한되었다. PIRL의 경우는 출력 고정된 크기의 representation을 내보내기 때문에 그럴 필요가 없으므로 최대 $9!\approx 3.6\mathrm M$개의 조합 수를 사용할 수 있다. 따라서, $\mathcal T$의 개수가 성능에 미치는 영향을 확인한다.

What is the effect of the number of negative samples?

The number of negative sample $N$이 성능에 미치는 영향을 확인한다.

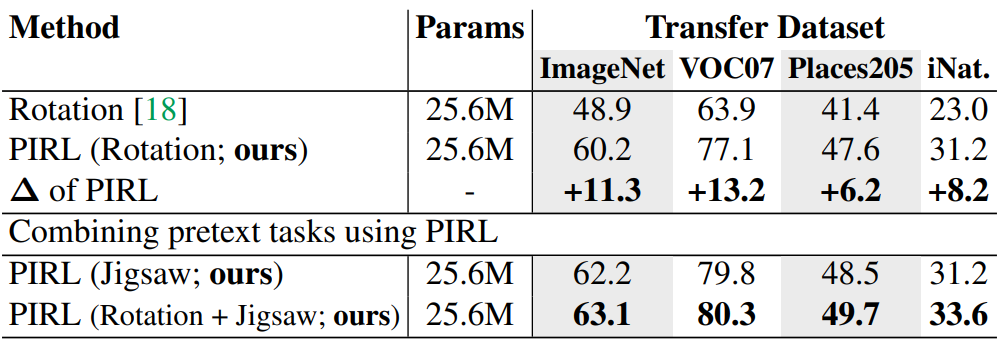
4.3 Generalizing PIRL to Other Pretext Tasks

다른 pretext task에도 PIRL을 사용될 수있는지 확인하기 위해 $\mathcal T=\{0^\circ, 90^\circ, 180^\circ, 270^\circ\}$인 rotation pretext task와, Rotation을 적용한 후 Jigsaw를 적용하는 multiple pretext task의 성능을 확인한다.

5. Related Work

• Image Reconstructing : sparse coding, adversarial training, autoencoder
• Pretext task in video : ordering video frame, tracking, cross-modal signal
• Pretext task in image : colorization,orientation/affine transform/relative position prediction, counting visual primitves(combinations)
• Invariant image representation : contrastive learning, clustering, maximizing mutual information

6. Discussion and Conclusion

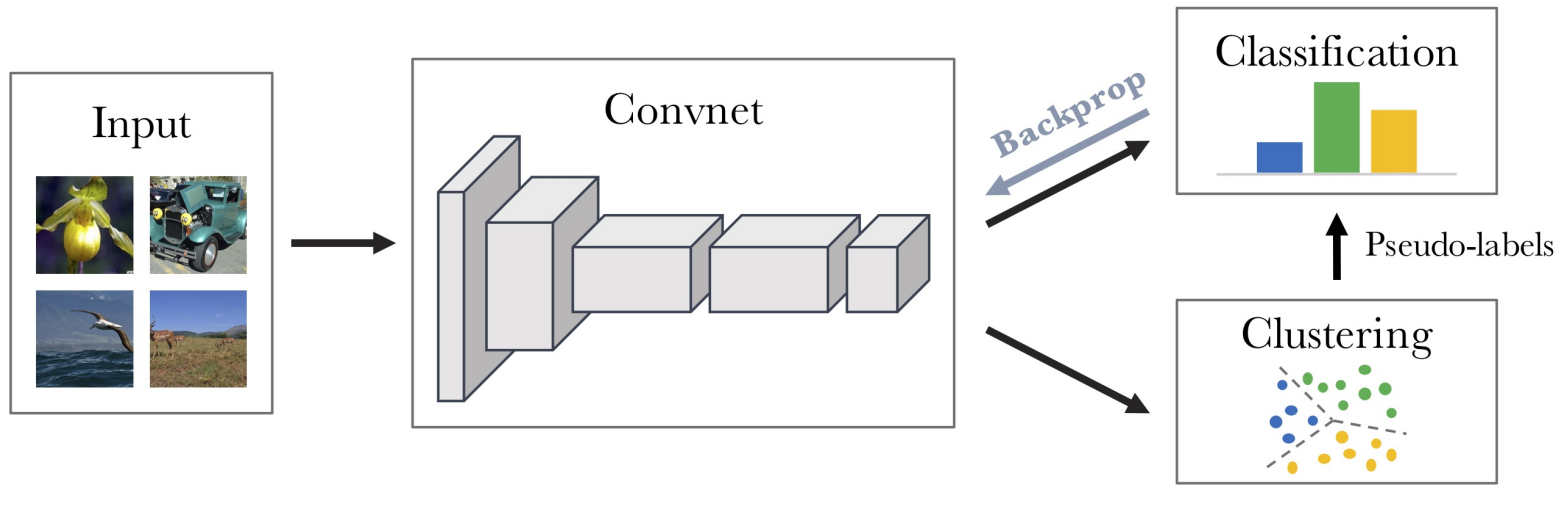
본 논문은 self-supervised pretext task에 적용된 이미지 변환에 invariant representation을 학습하는 PIRL을 연구했다. 기존의 다른 연구들보다 월등한 성능을 보였고, supervised learning method보다 뛰어난 성능을 보이기도 했다. 논문에서는 Jigsaw와 Rotation pretext task에서 연구를 수행했고, 두 개를 모두 사용한 pretext에서 최고성능을 보였다. 추후 clustering-based approach와 PIRL을 결합한 연구를 진행할 계획이다.