Deep Residual Learning for Image Recognition

관련 링크 : https://arxiv.org/abs/1512.03385

Architecture : ResNet(2015)

Abstract

층이 깊어지면 발생하는 문제를 residual 함수를 이용해서 해결했다.

1. Introduction

인공 신경망은 다양한 수준의 특징들을 학습하고, 이 다양성은 층이 깊어질수록 풍부해졌다. 하지만 층이 깊어지면서 gradient vanishing/exploding 문제가 발생했다. 이런 문제는 normalization layer와 normalized initialization으로 어느정도는 해결 할 수 있었고, 수 십층까지는 학습이 가능해졌다.

하지만 층이 더 깊어지면, degradation문제가 발생했다. 이는 깊은층을 가진 인공신경망이 오히려 더 낮은 성능을 보이는 것으로, 이는 overfitting이 아닌 구조적인 문제다.

위 사진은 degradation문제를 나타낸다. 만약 overfitting이 원인이였다면 test error에서는 다른 양상을 보이겠지만 그렇지 않음을 볼 수 있다. 성능을 낮추지않고 층을 늘리는 방법은 추가되는 층을 모두 identity mapping하는 것인데, 이는 단지 얕은층의 출력을 그대로 내보내는 것이므로 Nonsense다.

따라서, 기존의 desired underlying mapping이 $\mathcal{H}(x):=\mathcal{F}(x)$라면, 이를 입력을 참조한 함수 $\mathcal{F}(x):=\mathcal{H}(x)-x$로 바꾼다. 이는 입력을 참조하지 않은 기존의 mapping보다, 입력을 참조한 residual mapping이 더 optimize하기 쉬울것이라는 가정에서 시작했다. 극단적으로 identity mapping이 우리가 가진 데이터를 가장 잘 표현한다면($\mathcal{H}(x)=x$), $\mathcal{F}(x)$를 0으로 fit하는게 $x$로 fit하는 것 보다 쉬울 것이다.

여기서 $A:=B$의 의미는 좌변이 우변으로 정의된다는 뜻이다. $1= sin^2(\theta)+cos^2(\theta)$와 비교했을때, 후자는 좌변과 우변이 같다고는 하지만 정의된다고는 하지 않는다.

위 그림에서 출력에 더해지는 부분을 identity shorcut connection이라 부른다. 이 과정은 추가적인 계산을 요구하지 않고 성능을 향상시켰다.

2. Related Work

Residual Representations

Residual Representation은 여러 곳에서 쓰이고 그 성능을 보였다. 이미지 인식에서도 Fisher Vector를 이용해 dictionary를 만들때 original vector를 사용하는것 보다 residual vector를 사용하는게 효율적임을 보였다.

dictionary를 만드는 방식은 Bag of the words로, 이미지에서 local feature를 뽑아 이 feature들을 대표할 수 있는 값으로 codebook을 만든다. 이때 대표값들을 word라고 하며, k-means clustering 방식으로 결정한다. 새로운 이미지가 들어오면, 그 이미지의 요소들을 word로 대체하여 이미지를 word의 히스토그램으로 나타내서 이미지의 유사성을 비교할 수 있다.(색상이 word라면, 사과의 경우 대표 word인 빨간색과 비슷한 색은 모두 빨간색으로 대체)

이때 word를 feature를 그대로 사용하면 BoW이고, 모델의 파라미터에 대한 feature 벡터의 편미분을 사용하면 Fisher Vector이다.

또 다른 예시로, 편미분 방정식을 풀때 사용하는 multi-grid method에서도 residuali nature를 아는 solver가 그렇지 않은 solver보다 빠르게 수렴했다.

위의 예시로 볼때 residual을 사용해서 변형하거나 전제조건을 주는게 최적화를 간단히 함을 알 수 있다.

Shorcut Connections

많은 이론들이 shortcut connection을 이용했다. 초기에는 입력을 바로 출력으로 연결시키는 linear layer를 추가한 것부터, Googlenet에서는 중간층이 보조 분류기로 직접 연결되었다. 또 다른 연구에서는 layer response, gradients, propagated error를 centering하기위해 shortcut이 이용되기도 했다.

우리와 같은시기에 진행된 연구인 Highway networks에서도 이런 shortcut이 이용되었지만, 우리가 parameter-free인 identity shortcut을 사용한것과는 대조적으로 데이터에 의존적이고 parameter를 가지는 shortcut을 이용했다. 따라서 shortcut이 0에 가까워지면 non-residual function을 이용하는 것과 마찬가지이므로 우리와는 큰 차이가 있다.

3. Deep Residual Learning

3.1 Residual Learning

$\mathcal{H}(x)$를 여러개의 층에 의해 구성된 underlying mapping이라고 하자. 만약 다수의 nonlinear layers가 복잡한 함수($\mathcal{H}(x)$)를 점근적으로 근사할 수 있다면, 그보다 덜 복잡한 residual 함수($\mathcal{H}(x)-x$)를 근사할 수 있음은 당연할 것이다. 하지만 근사할 수 있는것과 그 난이도가 같은것은 다른 문제다.

우리는 앞서 Degradation 문제를 관찰하면서, 추가된 층들이 차라리 identity mapping이었다면 성능이 더 나빠지지는 않았을 것이라는 반직관을 얻었으므로 함수를 변형했다.

성능을 저하시키지 않으면서 층을 늘리는 방법은 identity mapping layer를 늘리는 것인데, 기존의 방법은 추가된 층을 identity mapping layer가 되도록 학습시키지 못했다(얕은층과 동일한 성능조차 보이지 못했으므로). 따라서 이 과정을 좀 더 쉽게 Residual fucntion을 0으로 만드는 문제로 바꿨다.

하지만 실제로 optimal한 mapping이 identity가 아닐 수 있다. 이 경우에 skip connection은 문제에 기준을 제시해 줘서 해결하기 쉽게 만든다.

만약 optimal mapping이 zero mapping보다 identity mapping에 가깝다면 optimize하기 더 쉽다. 실험을 통해서도 identity mapping이 일반적으로 작은 response를 이끌어 내서 의미있는 기준을 제시했음을 확인했다.

3.2 Identity Mapping by Shortcuts

Shorcut은 다음과 같이 구현했고, 입력과 출력의 차원이 다른 경우에만 $W_s$로 차원을 맞춰주었다. $\mathcal{F}(x, { W_i})$가 하나의 층만 가진다면 Linear와 동일해 Residual Learning의 이점이 사라지므로 두개 이상의 층을 가져야 한다. 입력과 출력의 차원만 맞춰준다면 $\mathcal{F}(x, { W_i})$는 어떤 연산도 가능하다.

\[y = \mathcal{F}(x, \{W_i\})+x \tag{1}\] \[y = \mathcal{F}(x, \{W_i\})+W_sx \tag{2}\]

3.3 Network Architectures

Plain Network는 VGG의 영향을 받아 3x3 filter를 사용했고, 입력과 출력의 resolution이 같도록 설계했으며, resolution이 반으로 줄면 channel은 두 배로 키웠다. Residual Network는 Plain에 shortcut을 추가하고, channel이 두배로 늘어나는 경우에만 1x1 conv를 이용해서 입력의 channel을 키워주었다.

VGG는 19.6 billion FLOPs, Plain Network와 Residual Network는 3.6 billion FLOPs이다.

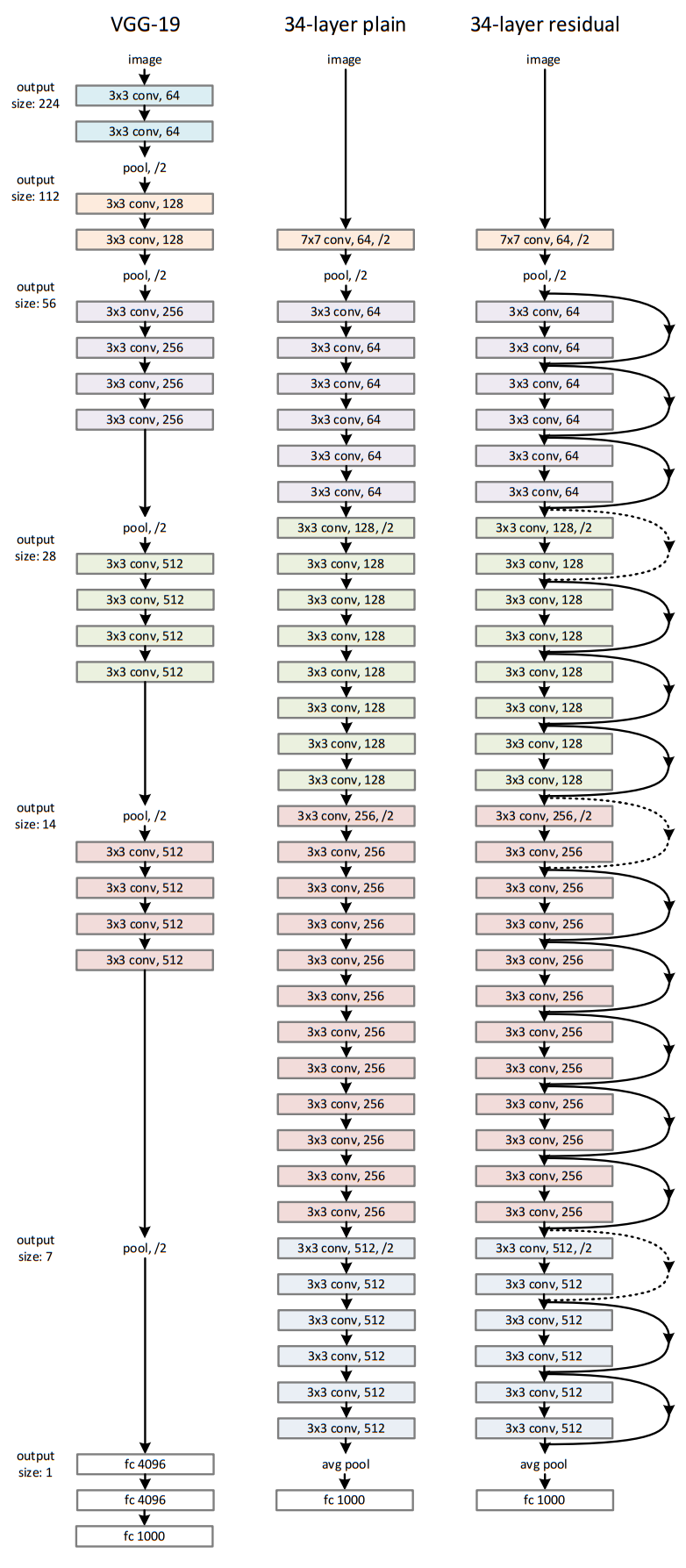
3.4 Implementation

VGG와 AlexNet에서 사용된 scale/color augmentation, per-pixel mean subtraction, horizontal flip을 이용해 data augmentation을 수행했다.

각각의 conv layer와 activation 사이에는 batch normalization을 사용하며, He initialization 기법으로 weight를 초기화하여 모든 plain/residual nets을 학습한다. batch normalization에 근거해 dropout을 사용하지 않는다.

learning rate는 0.1에서 시작하여, error plateau 상태마다 rate를 10으로 나누어 적용하며, decay는 0.0001, momentum은 0.9로 한 SGD를 사용했다. mini-batch size는 256로 했으며, iteration은 총 600K 수행된다.

비교를 위해 AlexNet의 standard 10-crop test를 수행했다. 최상의 결과를 내기 위해, VGG와 He initialization에서 사용한 fully-convolutional form을 적용했으며, multiple scale에 대한 score를 평균했다. multiple scale은 shorter side가 {224, 256, 384, 480, 640} 되도록 rescaling했다.

4. Experiments

4.1 ImageNet Classification

ImageNet 2012 clasification dataset을 이용했다.

Plain Networks

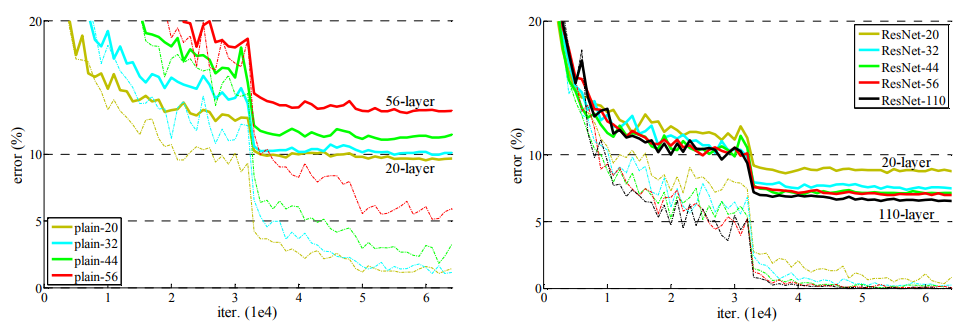
18-layer와 34-layer를 비교해보면, 34-layer는 18-layer보다 더 높은 validation error를 보인다. 이는 training시에도 동일했다. 학습시 BN과 He initialization을 이용했고, 학습을 관찰한 결과 gradient vanishing은 발생하지 않았으므로 구조적인 문제이다.

34-layer가 충분히 낮은 error를 보여줬으므로 많은 iteration후에는 더 좋은 성능을 보일까 하는 의문이 들 수 있지만, 논문에서는 충분히 많은 iteration에서도 degradation이 관찰되었다고 한다.

Residual Networks

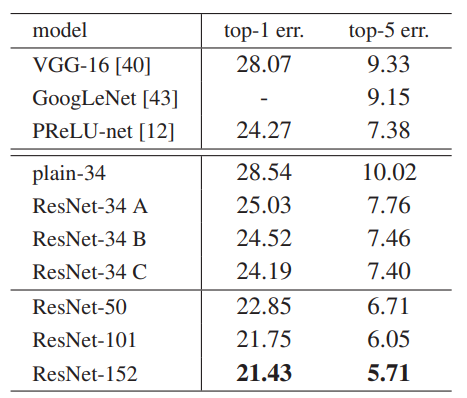
Fig. 4와 Table 2를 비교했을때 세가지를 관찰할 수 있다.

1. Residual Networks에서는 degradation 문제가 해결되어 깊은 네트워크의 성능이 더 좋다.
2. Residual Networks가 Plain Networks보다 성능이 더 좋다.
3. Plain 18-layer와 Residual 18-layer를 비교했을 때 Residual이 더 빠르다.

Identity vs. projection Shortcuts

Table 3에서, (A)는 zero-padding shortcuts으로 차원을 증가시켜 parameter-free한 것, (B)는 차원을 증가시킬때만 projection shortcuts을 이용한것, (C)는 모두 projection shortcuts을 사용한 것으로 성능은 (C)>(B)>(A)이다. (A)와 (B)를 비교해보면, zero-padding된 값들은 residual learning의 이점을 이용하지 못해 (B)>(A)이고, (B)와 (C)를 비교하면 더 많은 parameter의 영향으로 (C)>(B)이다. 하지만 세 경우의 성능차이가 미미하므로 논문의 나머지에선 시간과 메모리의 절약을 위해 (C)는 사용하지 않는다.

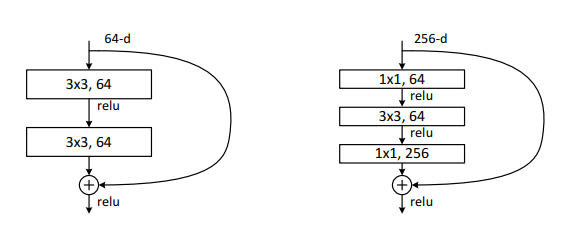
Deeper Bottleneck Architectures

2-layer를 3-layer로 대체하는데, 이는 연산시간을 줄이기 위해서이다.

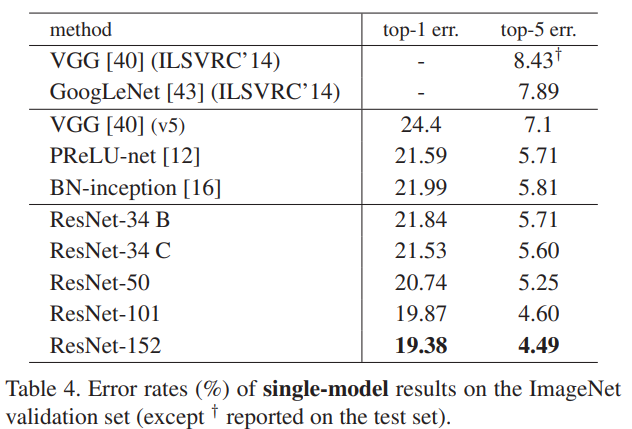
최종 모델의 구성은 다음과 같다.

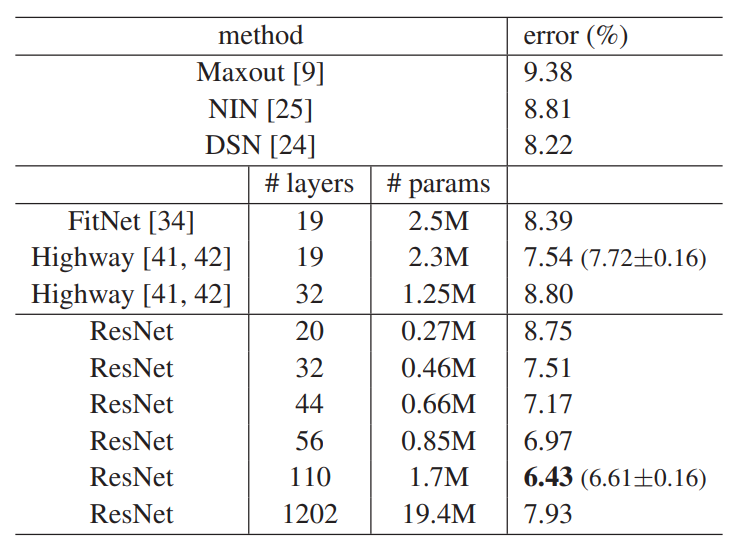
Comparisions with State-of-the-art Methods

4.2 CIFAR-10 and Analysis

CIFAR-10 dataset를 이용해 더 많은 연구를 수행는데, 이는 extremely deep network에 초점을 둔 연구이기에 다음과 같이 총 6n+2개의 stacked weighted layer로 구성된 간단한 architecture를 사용했다.(맨 마지막은 FC)

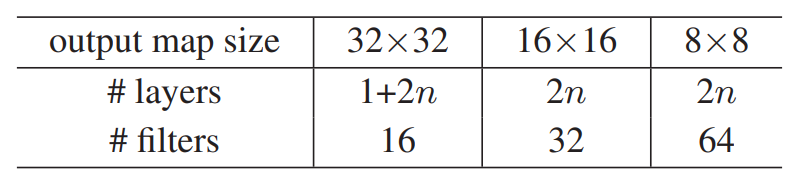
• shortcut connections은 각 3x3 layers 두 개마다 하나씩 사용했고(6n), identity mapping만 사용했다.
• He initialization으로 weight 초기화를 수행했고, weight decay는 0.0001, momentum은 0.9이다.
• 2개의 GPU에서 mini-batch size를 128로 했으며, 총 64000번의 iteration 동안 학습한다.
• learning rate는 0.1부터 시작하여 32000/48000번 째 iteration에서 rate를 10으로 나누어 적용한다.
• training시 4개의 pixel이 각 side에 padding되고, padded image와 horizontal flip 중에서 무작위로 32x32 crop을 샘플링 하여 data augmentation을 수행했다.
• testing시 32x32의 원본만 사용했다.

n=18일때는 learning rate 0.1이 너무 커서 0.01로 시작해서 error가 80%보다 작아질때 0.1로 올려주었다. 결과적으로 degradation문제를 해결하면서 다른 최신 네트워크보다 더 적은 파라미터를 가지고 좋은 성능을 보였다.

아래 그림에서 plain-110은 error가 60%가 넘어서 표시되지도 않았다.

Analysis of Layer Response

ResNet이 이에 대응하는 plain network보다 일반적으로 작은 response를 보여준다. 이는 residual function이 non-residual function보다 일반적으로 0에 가까울 것이라는 저자들의 basic motivation을 받쳐주는 결과이다. 또한, ResNet의 depth가 깊을 수록 더 작은 response를 보이는 것을 알 수 있다.

Exploring Over 1000 layers

이 모델은 110-layer ResNet과 비슷한 training error를 보였음에도, test 성능이 110-layer ResNet에 비해 뒤떨어진다. 논문에서는 CIFAR-10과 같은 소규모 dataset에는 1202-layer ResNet(19.4M param)과 같은 모델이 불필요하게 크므로 overfitting 때문이고, maxout이나 dropout과 같은 강력한 regularization 기법을 결합한다면 향상된 결과를 얻어낼 수 있다고 주장한다.

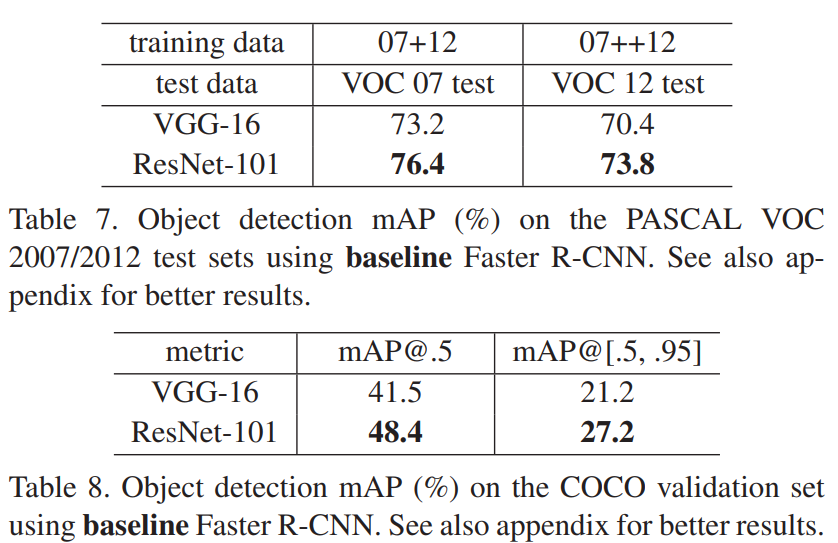
4.3 Object Detection on PASCAL and MS COCO

ResNet은 image recognition에도 좋은 성능을 보였는데, Faster R-CNN을 사용하고 VGG-16을 ResNet-101로 대체했을 때 성능향상을 이끌어냈다.