CoAtNet: Marrying Convolution and Attention for All Data Sizes

관련 링크 : https://arxiv.org/abs/2106.04803

• Conv와 Attn을 합치는 방법을 제안
• 제안한 방법들의 적절성을 스스로 보임

Intro

ViT는 JFT 300M 같은 대용량의 데이터셋을 이용했을 때 높은 성능을 보이지만, 이 보다 작은 데이터셋을 사용하면 ConvNet에 밀린다. 이런 경향은 ViT를 응용한 대부분의 모델에서 발생하고, 이는 ConvNet의 Locality 같은 Vision에 적절한 Inductive Bias의 부재를 많은 양의 데이터와 연산으로 보충하는 것으로 해석된다. 그러므로 ConvNet의 Locality를 ViT에 넣으려는 연구들이 진행되는 것은 당연하다고도 할 수 있다.

ViT 계열은 대용량의 데이터셋에서 좋은 성능을 보여주지만 학습이 어렵고 성능면에서 낮은 Lower Bound를 가지고 있고, ConvNet은 Vision에서 좋은 효과를 발휘하는 Inductive Bias를 가지고 있어 Local Pattern을 잘 파악해 일반화 성능이 높다. 그리고 각 모델의 이런 장점들은 모델을 구성하는 Self-Attention의 Input-Dependant Weighting과 Convolution의 Locality 때문이다.

따라서 이전 연구들은 ConvNet에 Self-Attention의 특징을, ViT에 Convolution의 특징을 추가하려는 방향으로 진행되었다. 하지만, ViT와 ConvNet의 장점이 뚜렷하므로 각각의 특징을 얼마나 주입해야 적절한지가 중요한데, 이전 연구들은 어떻게 주입할지에만 관심이 있었다. 오늘 소개할 논문은 각 모델들의 장점들을 고려해 어느 정도가 적절한지 연구하고, 이를 토대로 새로운 형태의 모델을 제안한다. 그럼 저자들의 방식을 살펴보자.

Conv vs. Attn

Conv와 Attn을 적절히 조합하는 문제는 두 질문으로 나누어 생각 할 수 있다. 첫 번째는 어떻게 Conv와 Attn을 한 Block으로 합칠 것인가?이고 두 번째는 다양한 Block들을 어떻게 합칠 것인가?이다. 먼저, 첫 번째 질문에 대한 답을 하기 위해 Conv와 Attn의 장점들을 살펴보자.

How to combine Conv and Attn within one Block?

Conv는 Locality와 Parameter Sharing라는 Vision에 적합한 Inductive Bias를 가지고 있다. Locality는 입력 이미지의 전체 픽셀을 고려하는게 아니라 일부 지역의 픽셀만 고려하는 특성을 말하고, Parameter Sharing은 Conv의 각 Weight가 이미지 안에서 입력 픽셀의 위치가 어디에 있는지가 아니라 Weight와 입력 픽셀의 상대적인 위치를 고려하는 특성이다. 쉽게 말하면 각 픽셀 위치에 적용되는 Conv Kernel의 Weight가 모두 공유됨을 말한다. 이 둘 덕분에 Conv는 Translation Equivalence의 특성을 가지고, 제한된 크기의 데이터셋에서도 좋은 일반화 성능을 가진다. Conv는 수식으로 다음과 같다.

\[y_i=\sum_{j\in \mathcal L(i)}w_{i-j}\odot x_j\]

$\mathcal L(i)$​​는 $i$​​의 이웃 픽셀들의 위치 Index의 집합으로 Locality를 뜻하고, 앞서 언급한 상대적인 위치를 고려하는 특성은 $i-j$​​​에서 나타난다. 논문에서는 Conv를 Depthwise에만 한정하는데, 이는 Attn의 FFN가 채널을 늘렸다가 줄이는 Inverted Bottleneck이 MobileNet의 MBConv와 유사하고, MBConv에 사용되는 Conv가 Depthwise이므로 한정했다고 말한다. 따라서 위 식도 Depthwise이고, 이 경우 $w_{i-j}$는 벡터지만 Depthwise로 한정한 이유가 타당해 보이지 않아 따로 명시하진 않았다.

이와 다르게 Attn는 Global Receptive Field를 가지며, 입력 데이터에 따라 달라지는 Adaptive Weighting을 Inductive Bias로 가진다. Global Receptive Field는 Vision에 적합 할 수 있지만 방대한 연산량으로 실용적이지 않아 Conv에서는 잘 사용되지 않았지만, 상대적으로 각 토큰(이미지에서는 픽셀 혹은 패치)들의 개수가 적은 자연어에서는 사용되었고, 따라서 Attn은 Global Receptive Field를 가진다. 떠 Input-Dependent한 Weight는 여러 Spatial Position들 사이의 복잡한 관계성을 잘 포착해 High-Level Concept를 처리하기 좋고, Conv의 Parameter Sharing과 Locality에 비하면 적은 제약을 가진 모델이라 Capacity를 증가시킨다. Attn은 수식으로 다음과 같다.

\[y_i=\sum_{k\in \mathcal G} \underbrace{\frac{\exp(x_i^\top x_j)}{\sum_{k\in\mathcal G}\exp(x_i^\top x_k)}}_{A_{i, j}}x_j\]

요약하자면, Conv는 Translation Equivariance를, Attn는 Input-adaptive Weighting과 Global Receptive Field를 장점으로 가지며 이를 모두 포함하기 위해 새로운 Block을 만든다. 이는 단순하게 Attn에 Global Kernel을 추가하면 가능하고, Attn에서 이는 Softmax 후와 전에 Global Kernel을 도입하는 두 가지 경우로 나뉜다.

1. Post Softmax

   \[y_i^\text{post}=\sum_{k\in \mathcal G}\left ( \frac{\exp(x_i^\top x_j)}{\sum_{k\in\mathcal G}\exp(x_i^\top x_k)}+w_{i-j}\right)x_j\]

2. Pre Softmax

   \[y_i^\text{pre}=\sum_{k\in \mathcal G} \frac{\exp(x_i^\top x_j+w_{i-j})}{\sum_{k\in\mathcal G}\exp(x_i^\top x_k+w_{i-k})}x_j\]

이렇게 하면 기존의 $A_{i,j}$​가 Input-adaptive한 특성을 살리면서도 Global Kernel $w_{i-j}$​에 의해 결정되어 앞선 장점들을 모두 가질 수 있다. 이런 방식은 Relative Positional Embedding과 유사하지만, 이 경우에는 각 층마다 다른 $w_{i-j}$​​​를 사용한다는 차이점이 있다. 논문에서는 최종적으로 두 번째, Pre를 주요 Block으로 사용하고 이후 Relative Attn이라 명명한다.

Ablation에서 Relative Attn의 여부에 따른 성능 비교를 수행한다. Relative Attn이 일반화 성능과 Capacity 모두에 좋음을 알 수 있다.

How to Stack different types of Blocks together?

첫 번째 질문을 해결 했으므로, 두 번째 질문을 해결할 차례다. Attn의 실용성을 해치는 가장 큰 원인은 토큰의 수(이미지에서 픽셀의 수)에 제곱으로 증가하는 연산량이다. 따라서 토큰의 수를 줄이거나, Attn의 연산 방식을 바꿔 연산량을 줄이는 방식들이 제안되었고 정리하면 다음과 같다.

1. Down-sampling을 통해 크기를 줄여 감당할 만한 수준에 이르면 Global Attn
2. Conv처럼 Local Field로 Attn의 범위를 제한한 Local Attn
3. Quadratic Attn을 여러 기법들을 이용한 Linear Attn으로 대체

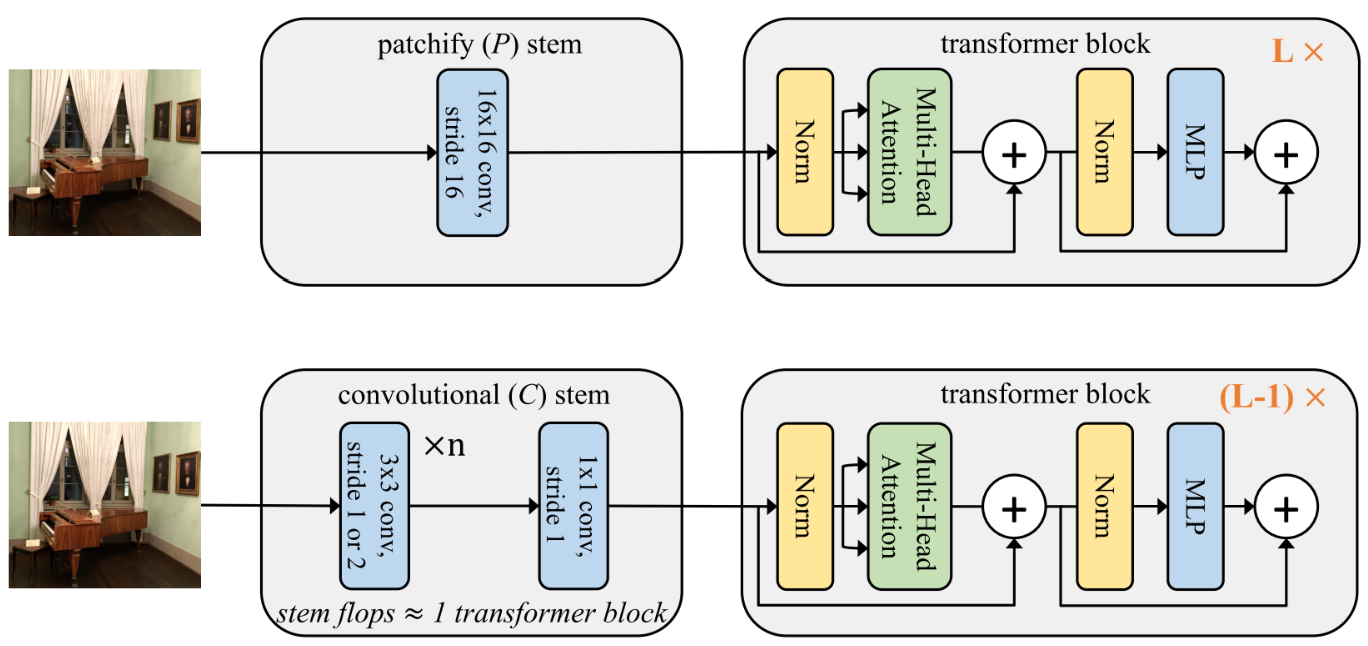
저자들은 2번과 3번 방식은 사용하지 않는다. Local Attn은 TPU상에서 비효율적이라 연산 속도를 올리기위한 목적을 달성할 수 없어 사용하지 않고, 3번의 경우는 예비 실험에서 좋은 성능을 보이지 못했다. 그래서 1번 방식만 고려한다. 하지만 1번 방식도 고려할 점이 충분히 많다. ViT의 경우는 이미지를 패치로 잘라 토큰의 수를 줄이는 방식을 사용했다. 간단히 ViT Stem이라 하자.

하지만 토큰의 수를 줄이는 방식이 굳이 ViT Stem일 필요는 없다. 일반적인 3X3 Conv를 쌓아서도 줄일 수 있다. 이 경우 ConvNet들이 그랬던 것 처럼 단계별로 Spatial Size를 줄이는 Multi-stage Layout을 사용한다. 저자들은 5 Stages의 모델을 만들고, $\text S0$​는 단순한 2층 Conv, $\text S1$​은 SE 모듈을 사용한 MBConv Block들로 이용한다. 그리고 Conv가 Local Pattern을 처리하는데 더 좋다는 사실에 근거해 초기 단계에 Conv가 많으면 좋으므로 $\text {S2-S4}$​는 다음의 $\text{C-C-C}$​, $\text{C-C-T}$​, $\text{C-T-T}$​, $\text {T-T-T}$​의 네 경우를 비교한다.

C는 SE 모듈을 사용한 MBConv Block만으로 이루어진 Stage를 의미하고, T는 위에서 만든 Relative Attn을 의미한다.

결과적으로 최선의 Stack 방식을 찾기 위해 기존 ViT Stem에 위에서 논의한 새로운 Attn을 사용한 $\text{ViT}_\text{REL}$​​과 Conv Stem을 사용한 Multi-Stage Layout(C와 T를 혼합한 4가지 방식)의 총 5가지 경우를 비교한다. 각 모델들은 Conv의 장점이었던 일반화 성능과 Attn의 장점이었던 높은 모델 Capacity의 관점에서 비교한다.

Capacity는 Overfit 없이 학습할 수 있는 데이터셋의 크기를 의미한다. Capacity가 큰 모델은 충분한 Training Step이 주어지고 난 후에 더 좋은 성능을 달성한다. 보통 파라미터 수를 키우면 Capacity가 커짐을 의미한다.

일반화 성능은 ImageNet-1K의 성능으로 비교 할 수 있다. 결과는 다음과 같다.

\[\text{C-C-C-C}\approx \text{C-C-C-T}\geq \text{C-C-T-T}>\text{C-T-T-T}\gg \text{ViT}_\text{REL}\]

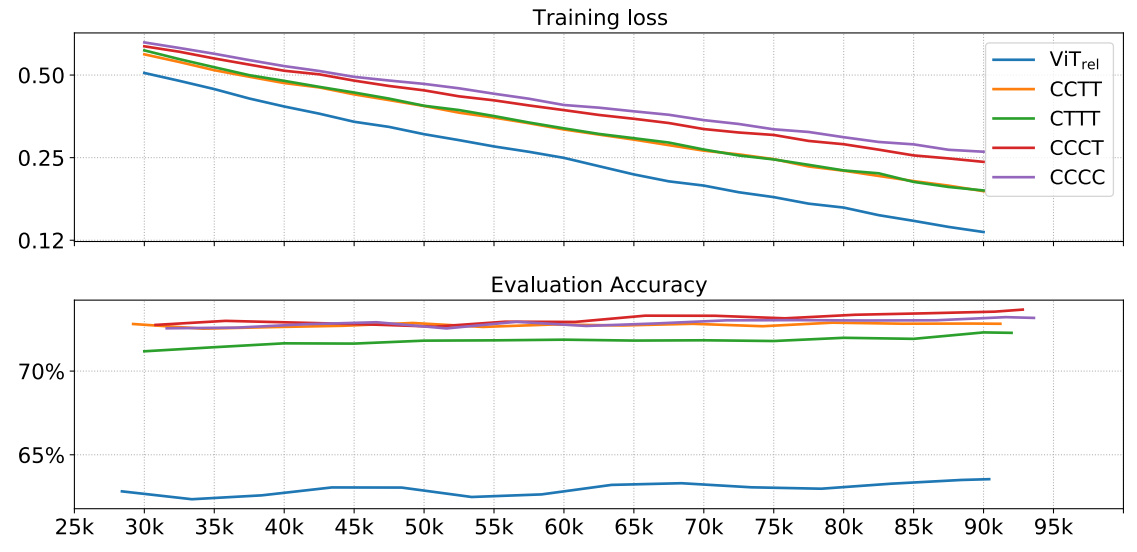
$\text S0$는 두 층의 Conv로 고정이므로, $\text{S1-S4}$까지를 각각 C와 T로 표현했다.

$\text{ViT}_\text{REL}$​의 경우 적절한 Low-Level Information Processing이 부족해 가장 일반화 성능이 떨어짐을 알 수 있다. 이는 Conv가 많을수록 일반화 성능이 좋아짐을 보면 더 명확해진다. Capcity에 대한 비교는 JFT-300M을 이용해 할 수 있다. 결과는 다음과 같다.

\[\text{C-C-T-T}\approx \text{C-T-T-T}>\text{ViT}_\text{REL}> \text{C-C-C-T}>\text{C-C-C-C}\]

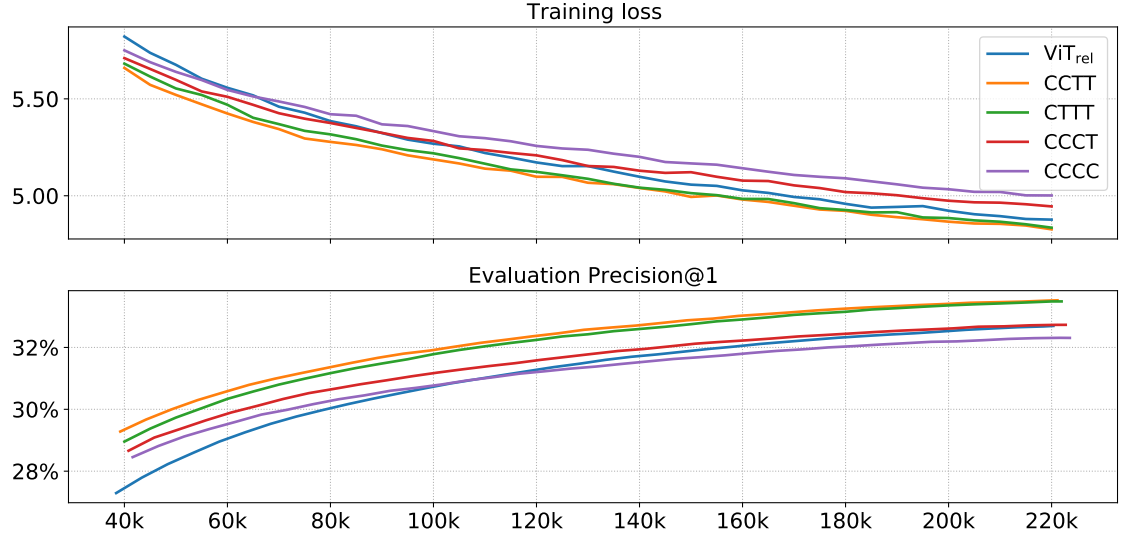
앞선 일반화 성능 결과와 유사하게 Transformer Block이 많으면 당연히 Capacity가 높을 것 같지만, 가장 Transformer Block이 많은 $\text{ViT}_\text{REL}$​​이 중간정도의 Capacity만 가짐을 알 수 있다. 이는 많은 Transformer Block이 Vision에서는 높은 Capacity를 얻기 위해서 필수적이지 않음을 뜻하거나, ViT Stem이 너무 많은 정보를 잃어버림을 의미한다.

두 관점에서 가장 적절한 모델은 $\text {C-C-T-T}$와 $\text{C-T-T-T}$​로 보이므로, 최종적으로 둘 사이에서 결정하기 위해 JFT pretrained 모델을 ImageNet-1K로 Transfer하는 Transferability 실험을 수행한다.

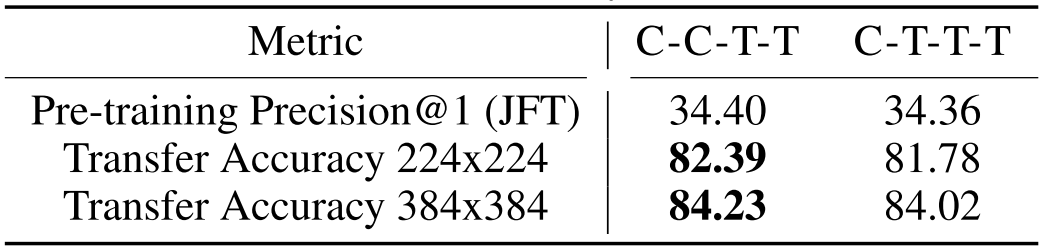
이때 $\text {C-C-T-T}$​​의 성능이 더 좋았으므로 최종적으로 이 방식으로 Block들을 쌓는다. 최종적인 모델은 다음과 같다.

연산의 대부분을 담당하는 부분은 $\text{S2, S3}$​이다. 따라서 이 두 Stage의 층 수와 차원 수에 따른 성능 비교도 Ablation에 존재하니 관심있으면 논문을 보자.

Results

다양한 실험들이 있지만, 결과는 다음의 하나만 보자.

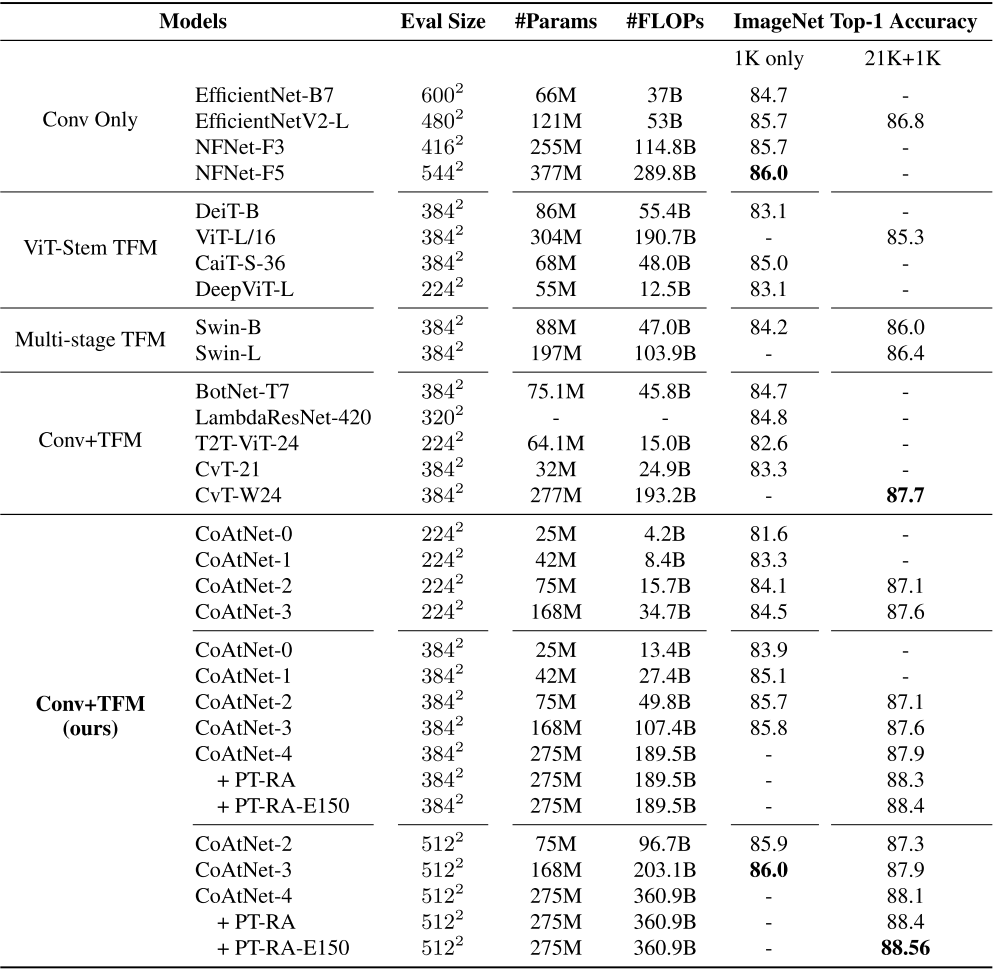
Conv Only 모델들과 비교 했을 때, ImageNet-1K에서도 SOTA 모델과 동일한 성능을 보였고, 21K pretrained를 1K로 Transfer 했을 때는 더 나은 성능을 보인다.

Remarks

Depthwise Conv로 Conv를 한정한 이유와, Conv와 Attn을 모두 사용한 모델을 만드는 질문을 두개로 쪼갠 이유가 공감이 잘 안되는 논문. 그래도 기존 Conv의 Inductive BIas를 Attn에 넣으려고 했던 연구들에 비해 체계적으로 비교한 것 같다. 이런 논문들을 보다 보니, Conv와 Attn 모두 Search Space로 넣은 Nas를 한번 찾아볼까 싶다.