관련 링크 : https://arxiv.org/abs/1912.02292
  • 고전적인 Bias-Variance Trade-Off와, 이와 다른 Double Descent를 포괄할 수 있는 가설 제시
  • 방대한 양의 실험으로 제시한 가설 Effective Model Complexity의 타당성을 보임
  • 이전에 다루어 지지 않은 Epoch-wise Double Descent와 Sample-wise Non-Monotonicity 현상을 발견

Intro

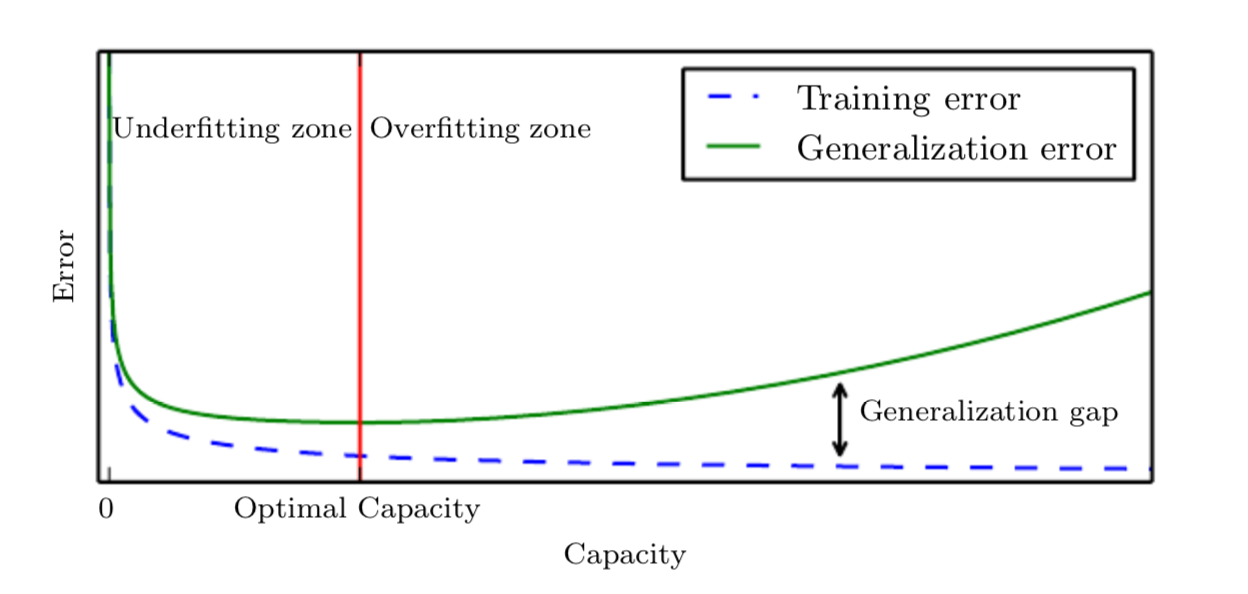
구글에 Bias-Variance Trade-Off를 검색하면, 다음 그림을 쉽게 볼 수 있다.

bias_variance

구글에서 볼 수 있는 위와 유사한 많은 그림들은 만든 사람에 따라 디자인이 차이가 날 수는 있지만, 공통적으로 Optimal Capacity 혹은 Optimal Model Complexity를 기준으로 Underfitting과 Overfitting으로 나뉘거나 High Bias와 High Variance로 나뉜다. 즉, 그림은 Optimal Capacity보다 작은 Capacity의 모델(High Bias)은 Underfit되고, 큰 모델(High Variance)은 Overfit될 수 있음을 보여준다. 이는 고전 ML에서 가장 잘 알려진 Bias-Variance Trade-Off이다. 이는 고전 ML에의 통념인 큰 모델이 더 별로다는 근거가 된다.

이 통념이 고전 ML의 역할을 이어받은 딥 러닝에서도 유효할까? 아래 그림은 여러 모델을 분석한 논문에서 가져온 그림이다. 이 그림은 모델의 복잡도와 연산량에 대한 성능을 나타낸다. 그림에서 상당히 많은 파라미터를 가진 VGG 계열들이 성능이 낮은걸 보면, 딥 러닝 역시 큰 모델을 싫어하는 걸까?

model_complexity_dl

원의 크기는 모델 파라미터 개수를 뜻한다.

아니다. VGG 계열이 상당히 예전 연구임을 감안하고 제외하고 다시 보자. 그러면 성능이 높은 모델들이 상대적으로 더 많은 파라미터를 가진다. 이는 딥 러닝 연구자들 사이에서 통용되는 큰 모델이 더 좋다는 통념의 약한 근거다. 도대체 뭐가 맞는걸까? 이를 확인하기 위한 가장 확실한 방법은 심층심경망의 파라미터 수를 기준으로 Bias-Variance Trade-Off 그림을 그려보는 것이다. 다행히 이를 먼저 수행한 연구가 있는데, 오늘 소개할 논문이다.

Model-wise Double Descent

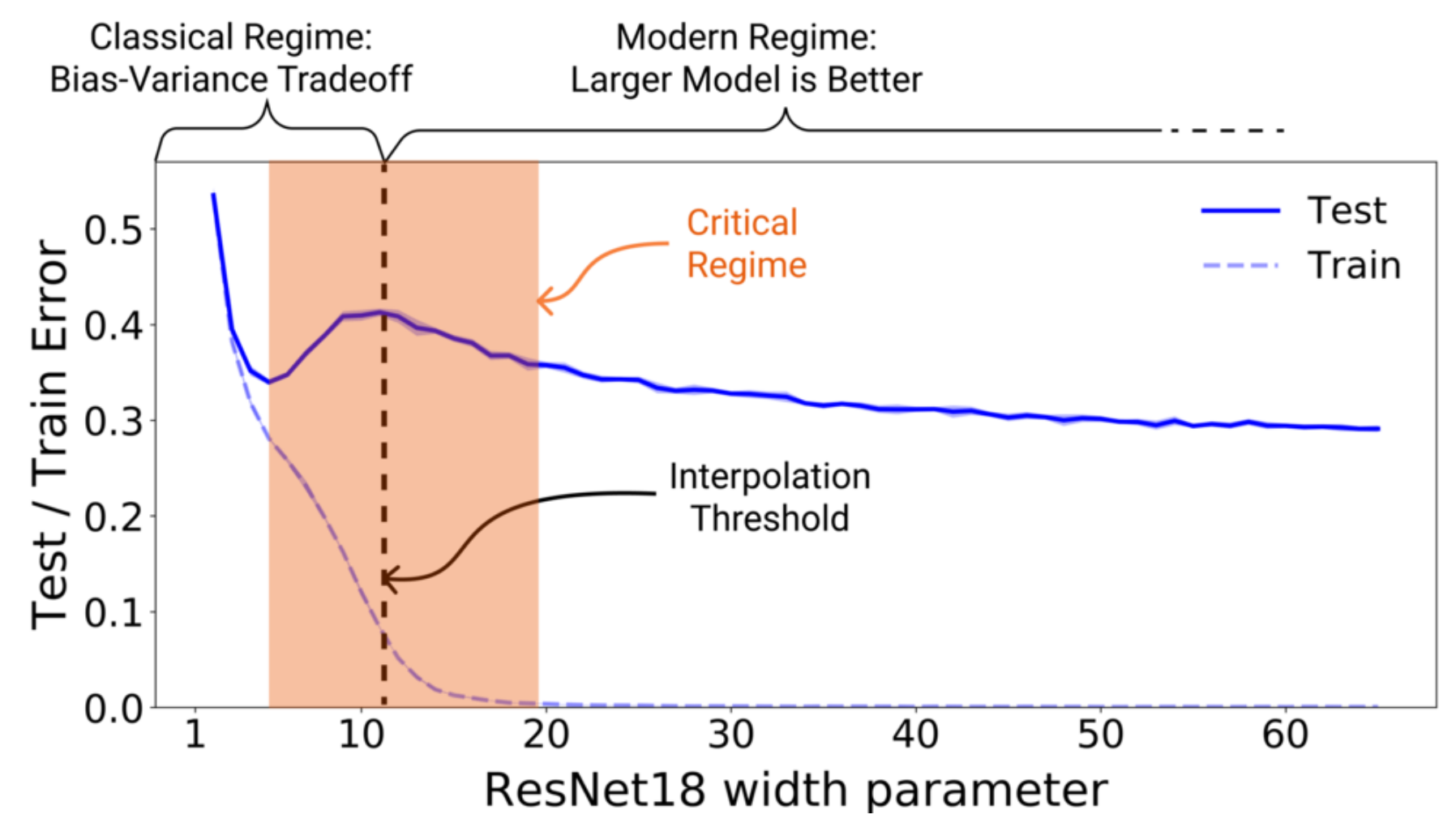
연구진들은 먼저 CIFAR-10 데이터셋을 이용해 모델의 파라미터 수에 대한 Train/Test Error 그래프를 그렸다. 모든 모델의 Training Epochs는 4K로 고정했다.

double descent

그림에 대해 이야기 하기 전에, 데이터셋의 라벨을 15% 확률로 오염시켰다는 점을 짚고 넘어가겠다. 이 논문은 다양한 환경에서 방대한 실험을 진행했고, 그 과정에서 라벨 노이즈가 강할수록 뚜렷한 Double Descent가 나타난다는 점을 발견했다. 따라서 Double Descent를 뚜렷하게 표현하기 위해 라벨 노이즈를 적용한 그림을 먼저 보여 준 것 같다.

결과 그래프는 꽤 신기한 현상을 보인다. 저자들이 Interpolation Threshold라 명명한 구간을 기준으로, 왼쪽은 전형적인 Bias-Variance Trade-Off를 보여주지만 오른쪽은 딥 러닝의 통념 큰 모델이 더 좋다를 보인다. 즉, 고전 ML과 딥 러닝의 통념들이 특정 지점을 기준으로 모두 나타나고 있다.

결과적으로, 고전 ML의 Trade-Off 관계가 딥 러닝까지 이어진다는 질문의 답은 Interpolation Threshold보다 작을때 그렇다이다. 그러면 자연스레 다음 질문이 떠오른다. Interpolation Threshold란 무엇일까? 위 그림을 보면 대답은 당연히 모델이 적절한 파라미터를 가지는 시점 일 것이다. 하지만, 이후 다른 실험에서 저자들은 모델 파라미터 수로는 설명할 수 없는 새로운 현상을 발견했다. 바로 Epoch-wise Double Descent이다.

Epoch-wise Double Descent

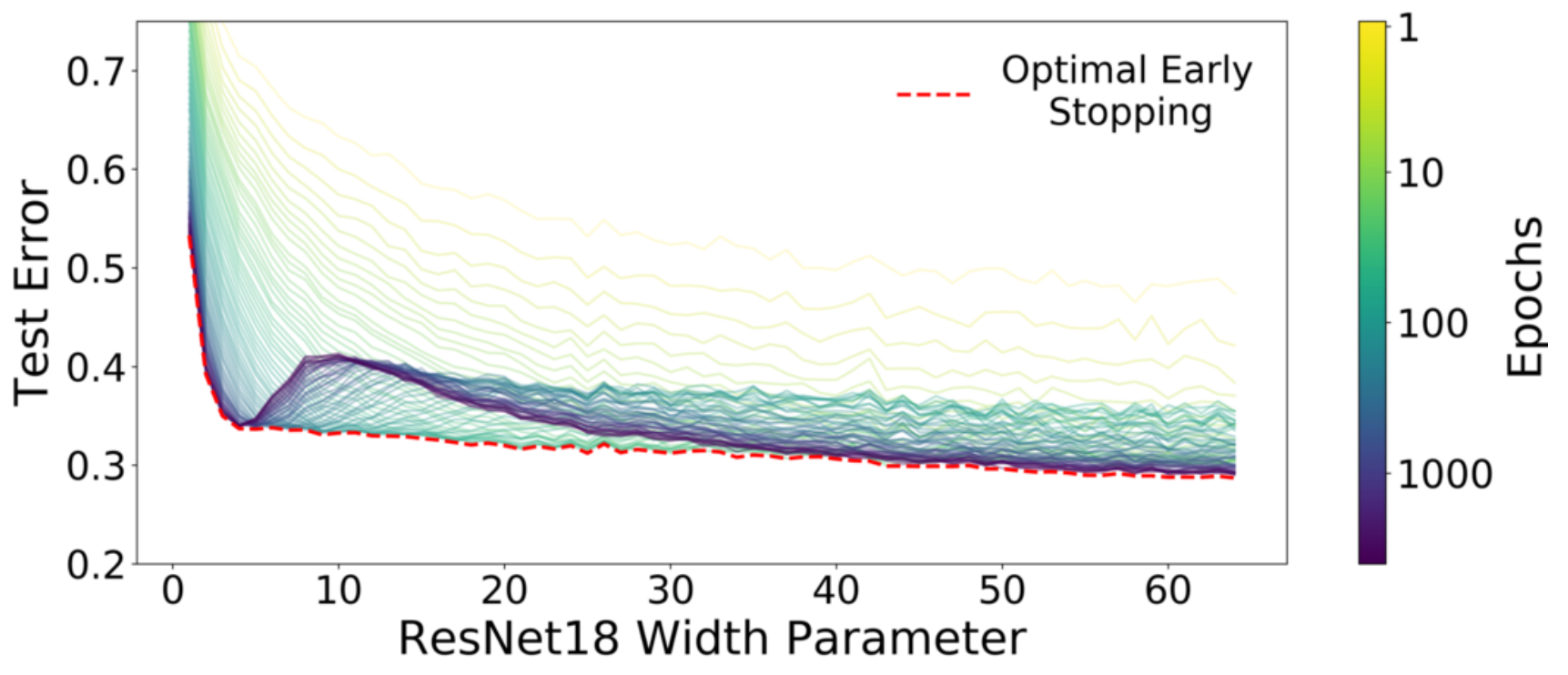
epochwise

Model-wise Double Descent 그림과 유사하게 Label Noise를 준 결과이다.

위 그림은 Training Epochs에 대한 모델의 Test Error를 나타낸다. 최대 Epochs에서의 Test Error는 앞서 본 그림과 유사하다. 주목할 부부분은 Optimal Early Stopping에서 최저 Test Error에 도달했다가 상승한 후 다시 감소하는 Epoch-wise Double Descent 현상이다. 위 그림에서는 이 부분이 Width가 30이상의 큰 모델에서만 나타난다.

epochwise_model

이 현상은 Optimizer나 LR Scheduler를 바꿔도 나타났다.

모델 파라미터별 Epochs에 대한 Test Error를 보면 확실히 큰 모델에서 이 현상이 두드러지며, 모델의 파라미터 수에 따라서 Epoch-wise Double Descent의 Interpolation Threshold가 다름을 알 수 있다. 모델 파라미터가 모델 복잡도라면, 모델의 성능 우열과 Interpolation Threshold 모두 Epoch에 따라 변하지 않아야 한다. 하지만 실제로는 그렇지 않다. 이는 모델 파라미터 외에도 모델 복잡도에 영향을 주는 다른 요인이 있다는 것을 의미한다.

Hypothesis

그렇다면, 모델 복잡도를 어떻게 정의해야 Model-wise와 Epoch-wise를 모두 설명할 수 있을까? 저자들은 복잡도를 학습 과정 전체인 $\mathcal T$에 대해 정의하고, 이를 Effective Model Complexity라고 정의했다.

\[\text {EMC}_{\mathcal D, \epsilon}(\mathcal T) :=\max \{n\;|\;\mathbb E_{\mathcal S \sim \mathcal D^n}[\text{Error}_\mathcal S(\mathcal{T(S))}]\leq \epsilon\}\]
  • $\mathcal{S\sim D^n}$: 분포 $\mathcal D$에서 $n$번 뽑은 라벨링된 데이터 셋 $\mathcal S$
  • $\mathcal{T(S)}$: 입력 데이터를 라벨로 맵핑하는 분류기

수식으로 나타내면 위와 같은데, 간단히 말하면 EMC는 $\mathcal T$의 Training Error가 0이 되기 위해 필요한 최대 샘플 수 $n$라고 할 수 있다. 이 가설을 이용해 $\text{EMC}_{\mathcal D,\epsilon}(\mathcal T)=n$인 Interpolation Threshold를 기준으로 위 영역들을 세개로 나눌 수 있다.

  1. Under-parameterized regime: $\text{EMC}_{\mathcal D,\epsilon}(\mathcal T)$가 $n$보다 충분히 작아서 EMC의 증가가 Test Error를 감소시키는 영역

  2. Over-parameterized regime: $\text{EMC}_{\mathcal D,\epsilon}(\mathcal T)$가 $n$보다 충분히 커서 EMC의 증가가 Test Error를 감소시키는 영역

  3. Critically parameterized regime: $\text{EMC}_{\mathcal D,\epsilon}(\mathcal T)\approx n$이라 EMC의 증가가 어떤 영향을 줄지 모호한 영역

    글의 순서가 논문과 달라, Critical Regime에서는 EMC의 영향이 모호하다고 한 점이 뜬금없이 느껴질 수 있다. 이는 논문을 보면 이해되는 부분이므로, 관심 있으면 논문을 보자.

이 가설을 이용해 Model-wise Double Descent를 설명해 보자. 파라미터 수가 많은 모델은 Training Error가 0이 되기 위해 많은 데이터가 필요하고 이는 EMC가 크다는 것을 의미한다. 따라서 EMC가 $n$보다 커 Over-parameterized 되어 모델의 파라미터 수를 늘려 EMC를 키워주면 Test Error가 낮아진다. 동일한 논리로 파라미터 수가 적은 모델은 EMC가 작아 Under-parameterized 되어 있으므로, Critically parameterized 되기 전까지 EMC를 키워주면 Test Error가 낮아진다.

Epoch-wise Double Descent도 유사하게 설명 가능하다. 동일한 크기의 모델을 작은 Training Epochs를 가지는 학습 과정 $\mathcal T$는 Training Error가 0이 되기 위해 필요한 데이터의 수가 적으므로 EMC가 작다. 반대로 Training Epochs가 큰 $\mathcal T$는 EMC가 크다. 따라서 Critical Regime을 제외하면 Model-wise Double Descent처럼 EMC와 비례해 성능이 증가한다.

Sample-wise Non-Monotonicity

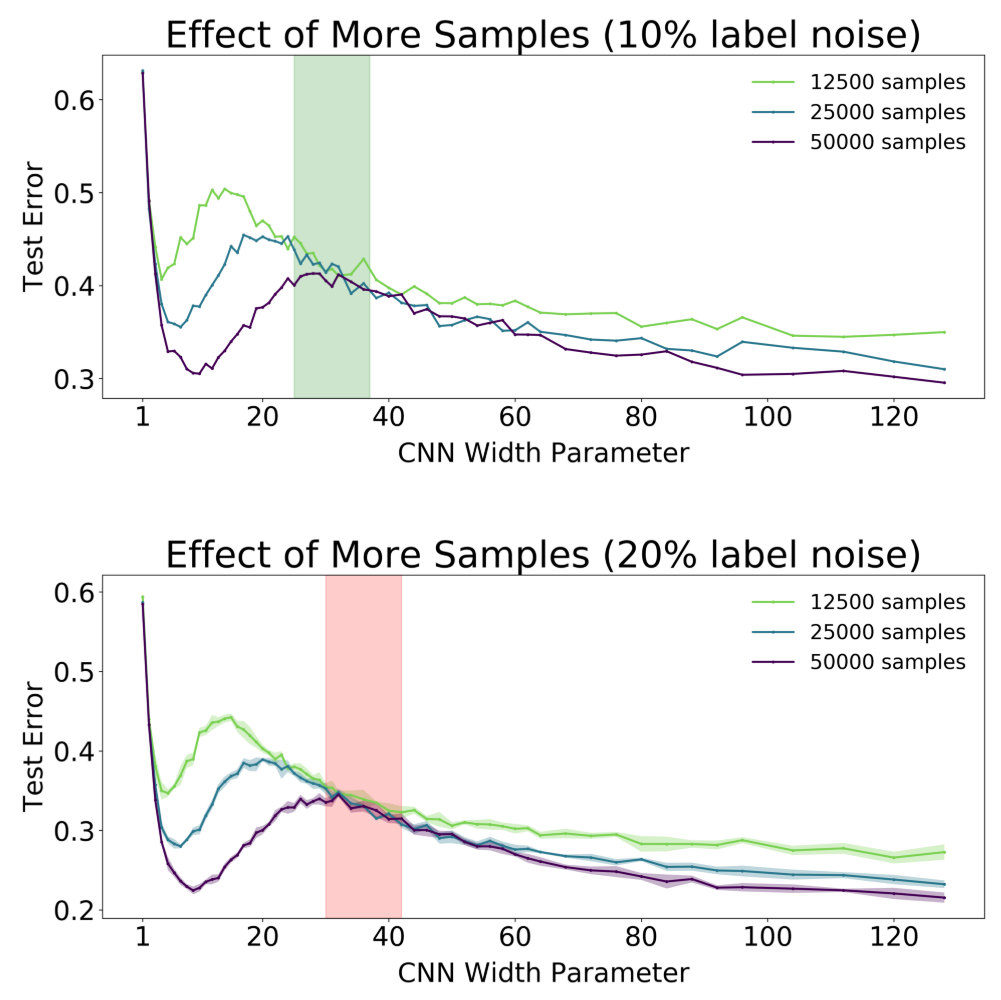
위에서 EMC를 도입해 Model-wise/Epoch-wise Double Descent에 대해 설명 했다. 그러면, $\mathcal T$를 고정하고 $n$을 변화시키면 어떨까? $\mathcal T$를 고정시켰으므로, $n$을 증가시키면 당연히 Over-parameterized regime이 Under-parameterized 될 것이다. 쉽게 말하면, Test Error가 최고점인 모델 파라미터 수의 위치가 오른쪽으로 이동할 것이다. 다음의 $n$별 모델 파라미터에 대한 Test Error를 나타내는 그림을 보면 예상과 동일하다.

samplewise

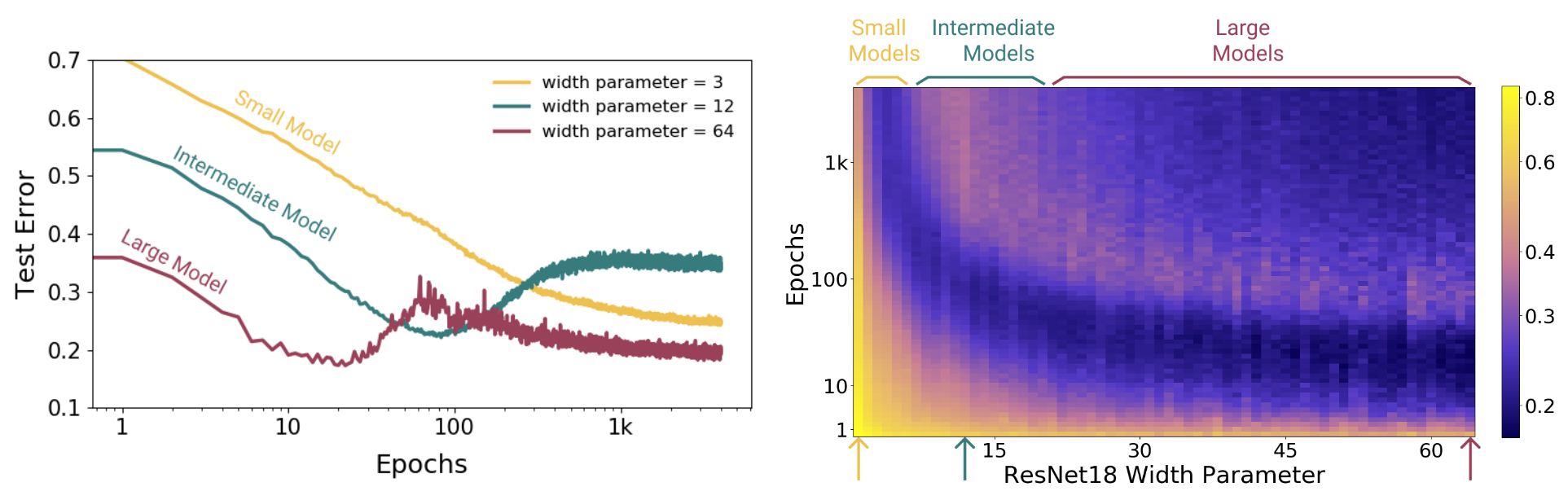
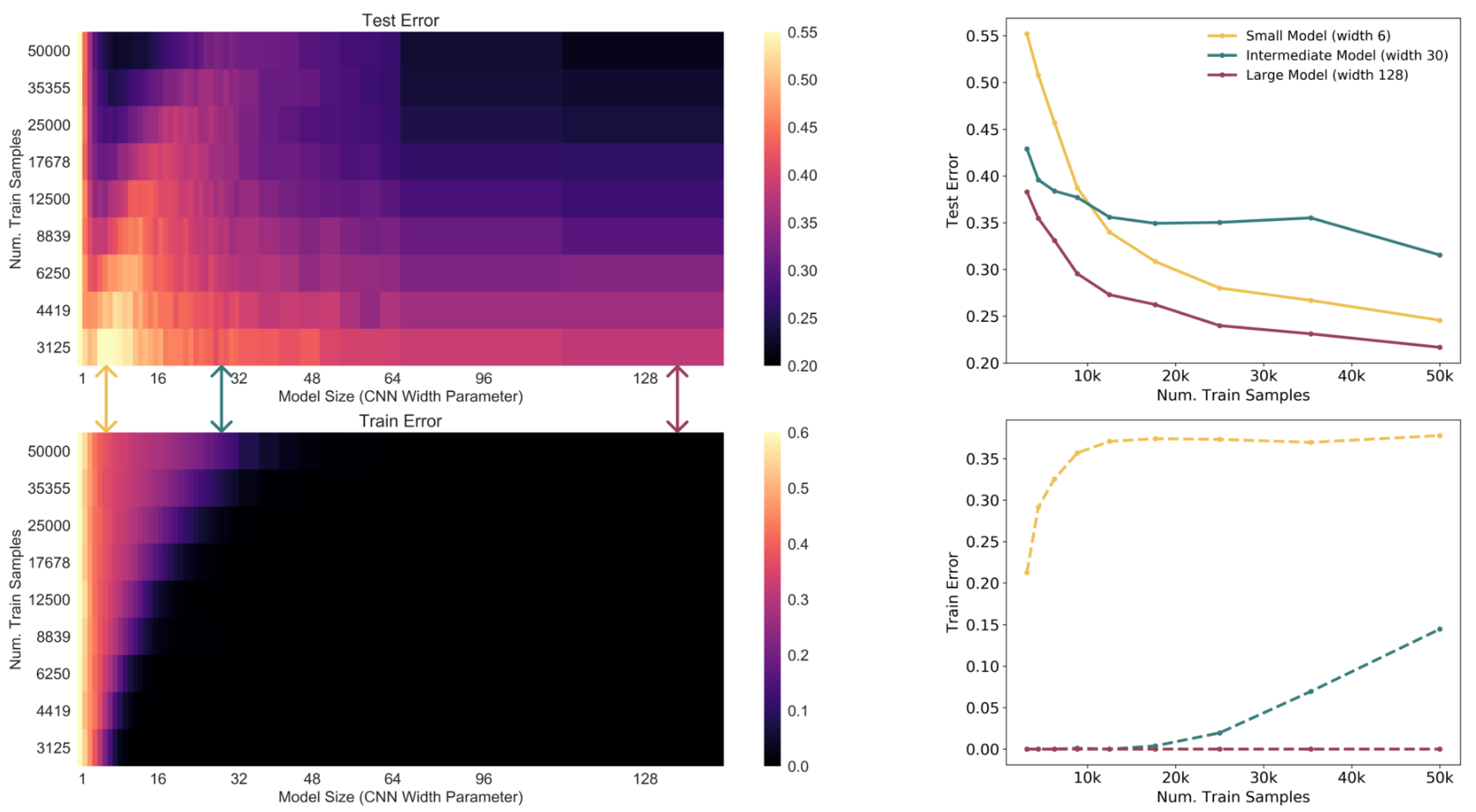
하지만 표시된 적색, 녹색 영역을 보면 더 많은 샘플이 오히려 낮은 성능을 보이는 구간이 있다. 이는 모든 딥 러닝 연구자들이 동의하는 데이터는 많을수록 좋다는 생각과는 다르다. 저자들은 이 현상을 Sample-wise Non-Monotonicity라고 명명했다. 이는 다음의 모델 크기별 $n$에 대한 Test Error 그림을 보면 더 명확하다.

non-monotonicity

그럼 왜 이런 현상이 나타날까? 이는 왼쪽 그림을 보면 명확해진다. 왼쪽 그림에 따르면, Small Model은 EMC가 $n=50000$에 비해 상당히 작고, Large Model은 상당히 크다. 따라서 앞서 제시한 가설대로 각각 Under/Over-parameterized 되었고, 많은 데이터가 더 좋다는 통념에 따라 Test Error가 감소한다고 볼 수 있다. 하지만 Intermediate Model은 EMC=50000으로 Critical Regime에 속한다. 따라서 이 근방에서 특정 요소의 변화는 예측할 수 없고, 위의 그림처럼 많은 데이터가 성능을 감소시키기는 경우도 발생한다.

Remarks

개인적으로 이 논문은 대부분의 연구자들이 단순히 생각하는 Bias-Variance Trade-Off를 딥 러닝으로 효과적으로 확장하면서 이후 여러 실험에서 고려해 볼 만한 많은 지점을 제인한 유용한 연구라고 생각한다. 정리하기 위해 누군가에게는 의미있거나 호기심을 이끌수 있는 많은 실험 결과들을 제외했음에도 꽤 적을게 많았던 것 같다. 가장 중요한 Critical Regime에 대해서는 완전히 알 수 없다고 못 박긴 했지만, 저자들의 가설은 현재까지 꽤 신빙성 있어 보인다. 후속 연구도 착실히 진행 됬으면…

Leave a comment

You may also enjoy