Not All Images are Worth 16x16 Words: Dynamic Vision Transformers with Adaptive Sequence Length

관련 링크 : https://arxiv.org/abs/2105.15075

• 이미지의 난이도에 따라 동적으로 Inference해 연산량을 줄이는 DVT 제안

Intro

ViT 이후로 Vision 분야에서 Transformer들이 등장하기 시작했다. 이들은 공통적으로 이미지를 패치로 나누어 문장의 단어처럼 토큰화 해주었는데, 토큰의 개수가 많아지면 토큰 수의 제곱에 비례해 연산량이 증가하지만 성능은 더 좋아지는 Trade-Off를 가지고 있었다. 따라서 보통 $14\times 14$ 혹은 $16\times 16$개의 토큰을 사용했다.

오늘 소개할 논문에서는 토큰의 개수를 이미지의 난이도에 따라 다르게 사용한다. 아래 표는 T2T-ViT-12에서 토큰 수에 따른 ImageNet 성능과 연산량이다.

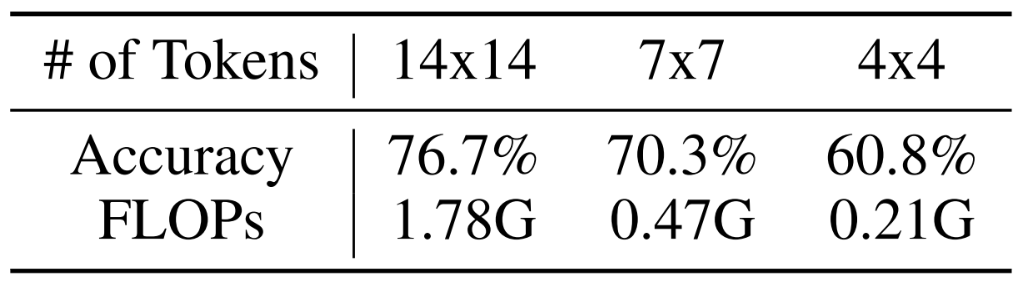
당연히 $14\times 14$개의 토큰을 사용한 모델이 $7\times 7$이나 $4\times 4$에 비해 성능이 높다. 하지만 이를 연산량까지 고려해 달리 보면, $60.8\%$의 이미지들은 $4\times 4$로도 충분하므로 $15.9\%$의 이미지에만 토큰 수가 많이 요구되고, 성능 향상을 위해 $\frac{1.78G}{0.21G}\approx 8.5$배의 추가 연산량이 필요하지 않다고 볼 수 있다. 따라서 저자들은 쉬운 이미지는 토큰 수가 적어도 충분히 쉽게 풀 수 있고, 어려운 이미지에는 많은 토큰 수가 필요하다고 생각해 이미지의 난이도에 따라 동적으로 Inference하는 Dynamic Vision Transformer(DVT)를 제안한다.

DVT

저자들의 생각을 듣고나면 어떻게 이미지의 난이도를 측정할 거고, 어떻게 동적으로 Inference할 지 의문이 든다. 이 두 의문을 해결하기 위해 Inference 과정을 대략적으로 살펴보자.

Inference

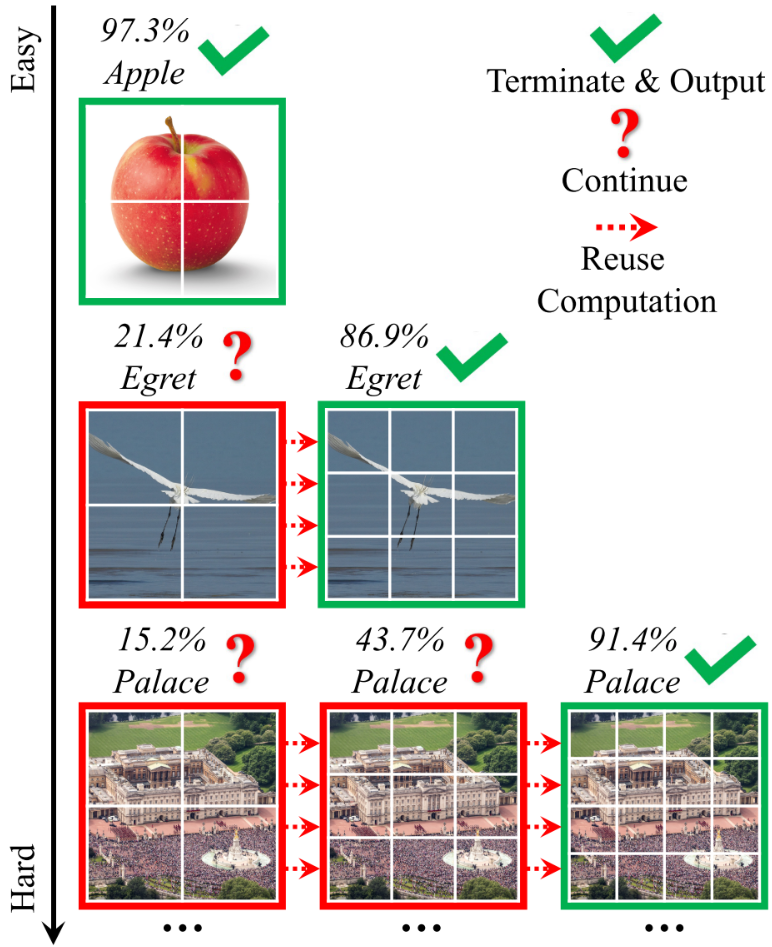
Inference 과정은 위 이미지와 동일하다. 첫 번째 행의 사과같이 쉬운 이미지는 4개의 토큰으로 잘라 4개의 토큰을 이용하는 Transformer에 통과시킨 후, 조건을 만족하면 Inference를 끝낸다. 마지막 행의 궁전 같은 어려운 이미지는 좀 다르다. 4개의 토큰으로는 15.2%의 Confidence 밖에 얻지 못했다. 따라서, 9개의 토큰으로 잘라 9개의 토큰을 이용하는 Transformer로 Inference하지만, 여전히 43.7%의 Confidence 밖에 얻지 못했고, 결과적으로 16개의 토큰을 이용하는 Transforemer로 Inference한 후에야 91.4%의 신뢰도를 얻고 Inference를 종료했다.

Confidence는 Softmax Prediction의 최대 값이다.

위 과정을 요약하면, 각 Transformer를 기준으로 먼저 Inference된 Transformer들을 Upstream Transformer라 하고 이 후 Inference될 것들은 Downstream Transformer라 할 때,

1. Upstream에서 Inference 후 Confidence가 특정 Threshold를 넘으면 종료
2. 넘지 않으면 Downstream에서 Inference

이고, 이미지의 난이도는 Confidence로 측정하고, Threshold를 이용해 동적으로 Inference한다로 앞선 두 의문에 답을 할 수 있다.

그러나 추가적으로 새로운 의문점들이 생긴다. Threshold는 어떻게 정할까? 또 모델이 어떻게 생겨먹었길래 저게 될까? Upstream에서 예측이 실패해서 Downstream에서 넘어가면 Feature map은 버려지나? 이것들을 설명하기 위해서 전체 모델과 Training 과정을 살펴보자.

Training

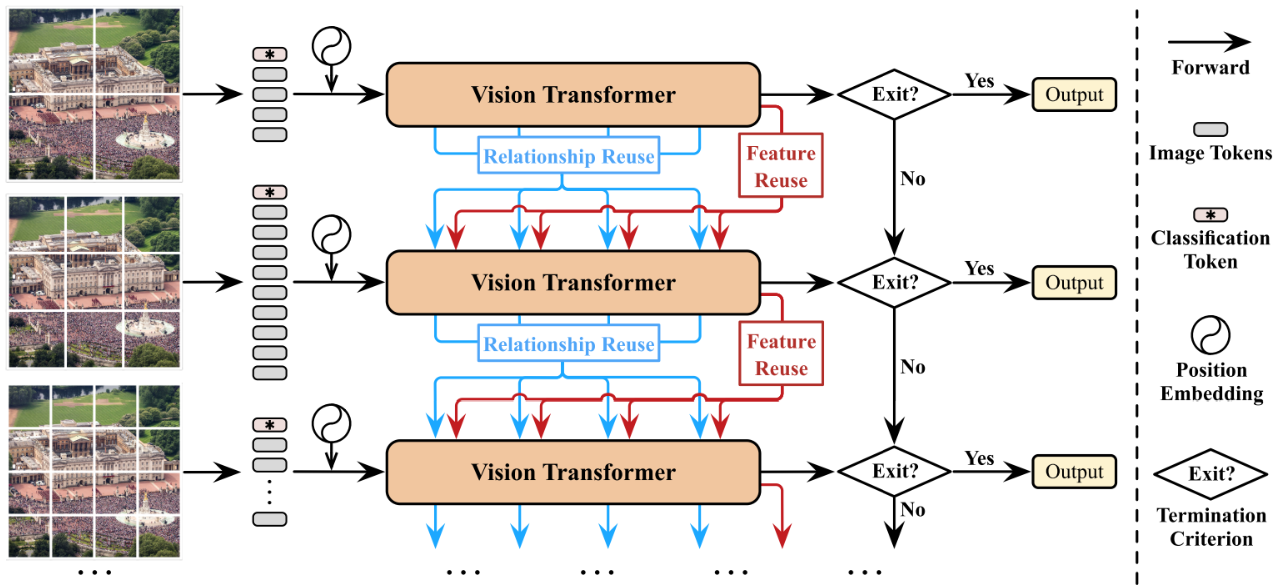
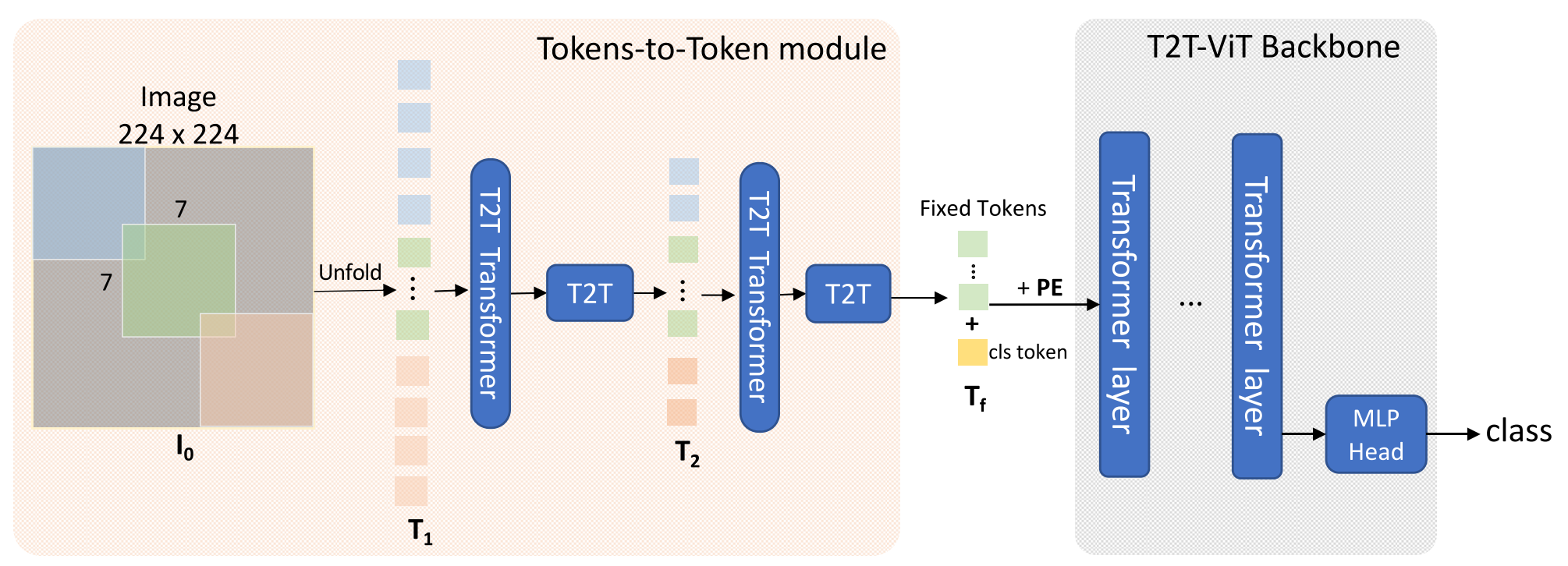
모델은 위와 같이 생겼다. Vision Transformer는 이전 연구들에서 사용된 것과 차이가 없으므로 크게 설명할 필요는 없고, 저자들이 추가한 Relationship Resue, Feature Reuse, Exit에 대해 설명해 보겠다.

Exit

사실 딱히 설명할 내용은 없는 부분으로, Threshold $\eta$을 이용해 Inference를 끝낼지, 계속 할 지를 결정하는 부분이다. $\eta$는 Transformer마다 하나 씩 개별 존재하므로, $\eta_i,i \in {1, 2, \ldots , I}$이다. $\eta_i$는 모델의 파라미터와 달리 Forward에 관여하지 못하고 미분 불가능하므로, Validation Set에 대해서 연산량에 $B$의 제한을 두어 다음 문제를 최적화 해서 찾는다.

\[\underset {\eta_1, \eta_2, \ldots} {\text {maximize}} \text { Acc}(\mathcal D_{\text {val}}, \{\eta_1, \eta_2, \ldots\}) \\s.t. \text { FLOPs}(\mathcal D_{\text {val}}, \{\eta_1, \eta_2, \ldots\}\leq B)\]

논문에서는 Genetic Algorithm을 이용해 찾았다고 한다.

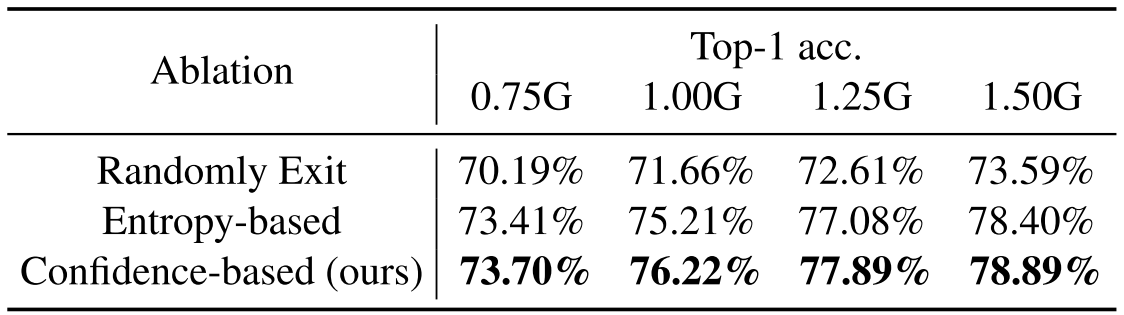
Exit는 Confidence말고 각 Exit을 무작위로 수행하는 등의 대안이 있을 수 있다. 이와 관련된 Ablation은 다음과 같다.

Reuse

Dynamic Inference를 위해서는 이미지의 난이도에 따라 다른 토큰 개수를 사용하는 Transformer들이 필요하다. 하지만, 이미지의 난이도 Confidence는 각 Transformer에 대해 Inference를 수행해야 알 수 있으므로, 어려운 이미지라 하더라도 바로 토큰 수가 많은 Transformer에 넣을 수 없고, 쉽든 어렵든 무조건 Upstream에 Inference 해야 한다.

따라서 Upstream에서 Confidence가 낮을 경우 Downstream에서 Inference 하는데, Downstream의 Feature만 사용하면 이전 Inference가 불필요해 지므로 이를 해소하고자 Upstream의 Attention Matrix인 Relationship과 Feature Map을 재사용한다. 먼저, Feature Reuse부터 살펴보자.

• Feature Reuse(Context Embedding)

  

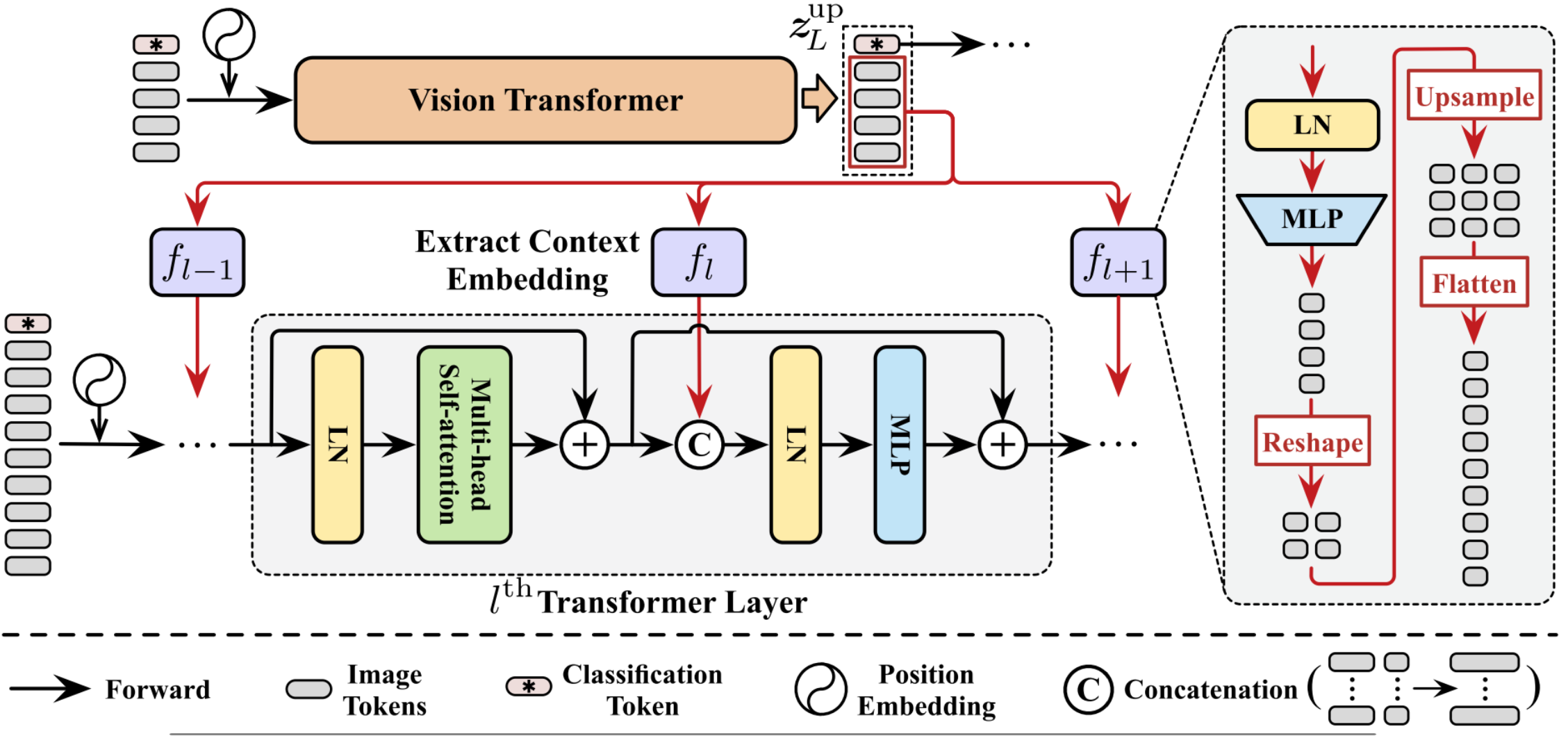
  Feature Reuse의 핵심은 Upstream의 Feature를 Downstream에서 사용하는 것이다. 따라서, Feature보다는 분류를 위해 사용했던 Classification Token을 제외하고, Transformer Layer의 입력으로 넣는 게 아닌 Self-Attention이 수행된 이후에 Concat해 주입한다.

  이때 Upstream과 Downstream의 토큰 개수가 다르므로 Feature Map을 바로 Concat 할 수 없으므로, Downstream의 모든 층마다 개별 Operation $f_l$을 이용해 토큰 개수를 맞춰 준다. 토큰 개수는 토큰들을 이미지 형태로 만들어서 Interpolation해 크기를 늘린 후 다시 잘라서 만든다. 결과적으로 Transformer Layer의 $\text{MLP}$에 들어가는 입력 차원 수가 Upstream Feature 만큼 늘어난다.

  저자들은 $f_l$을 구현할 때 내부의 $\text{MLP}$가 입력의 차원을 감소($128 \rightarrow 48$)시키도록 했다.

  위 그림의 Transformer Layer Forward를 식으로 나타내면 다음과 같다.

  1. $z_l’\in \mathbb R^{N\times D}=\text{MSA}(\text{LN}(z_{l-1}))+z_{l-1}$
  2. $z_l\in \mathbb R^{N\times D}=\text{MLP(LN(Concat(}z_l’, \mathbf E_l=f_l(z_L^\text{up})\in \mathbb R^{N \times D’}))) +z_l’$

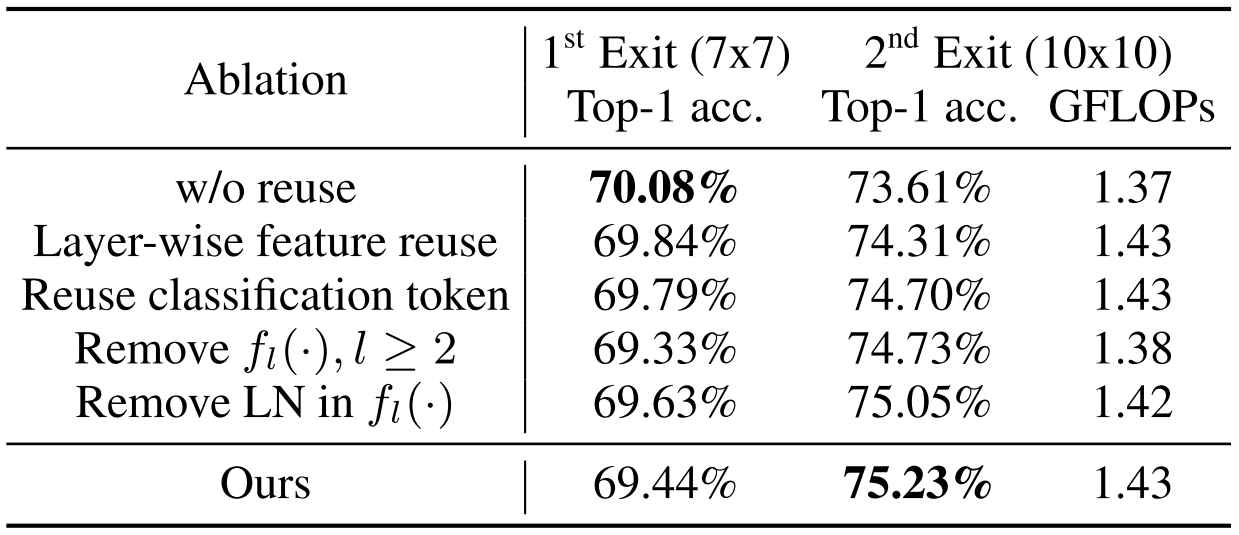
  여기서, Upstream과 Downstream Transformer들의 층 수 $L$은 동일하므로 제일 마지막 Feature가 아니라 각 층마다 사용하면 어떨까?라는 의문이 들 수 있다. 이와 관련된 Ablation은 다음과 같다.

  

• Relationship Reuse

  

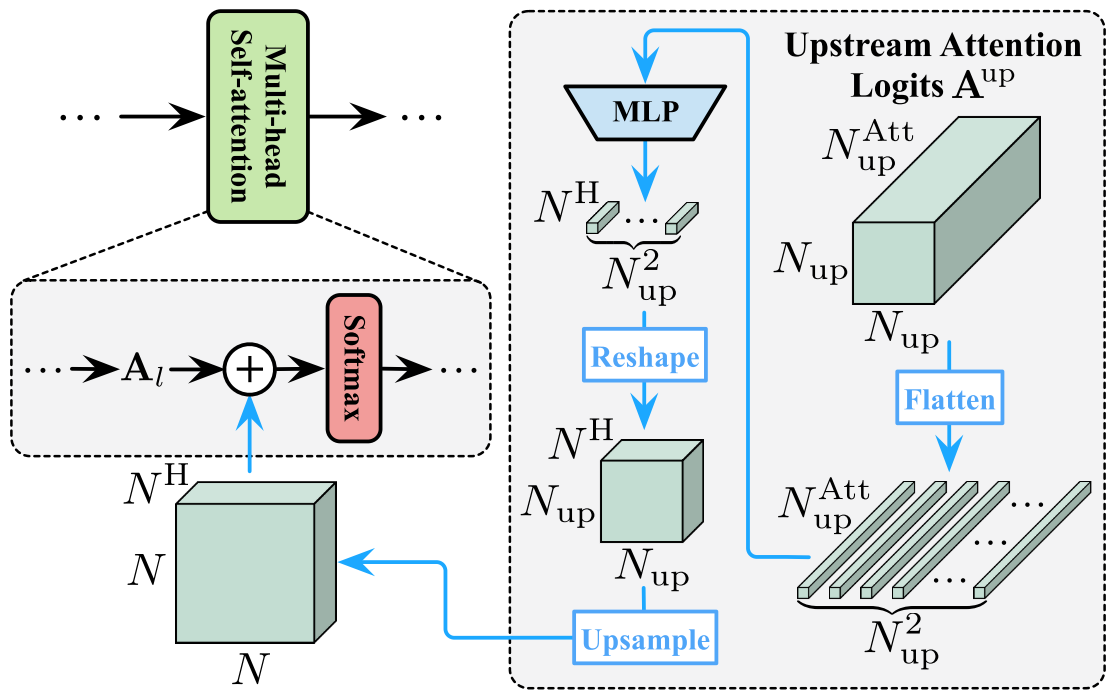
  Relationship도 Feature Reuse와 유사하다. 차이는 Multi-head Self-Attention 연산에 관여하고, 마지막 층의 Relationship만 사용하는 게 아니라 모든 층의 Relationship들을 Concat해서 사용한다. Relationship도 Feature와 동일하게 개별 Operation $r_l$을 이용해 토큰 수를 맞춰 준다.

  실제 구현에서는 효율성을 위해 Feature Reuse와 달리 각 층마다 $\text {MLP}$를 배치하지 않고, 각 Transformer마다 하나의 $\text{MLP}$를 배치해 $N_\text{up}^\text {Att} \rightarrow 3N^\text HL\rightarrow N^\text HL$ 한 번에 계산 한 후 층 별로 나눈다. Official Code를 보면 다음과 같다.

  relation_reuse_conv = nn.Sequential(
    nn.Conv2d(
      num_heads * depth, num_heads * depth * 3, 
      kernel_size=1, stride=1, padding=0, bias=True),
    GELU(),
    nn.Conv2d(num_heads * depth * 3, num_heads * depth, 
    kernel_size=1, stride=1, padding=0, bias=True)
  )
  

  따라서 $\mathbf A^\text {up}=\text {Concat}(\mathbf A_1^\text{up}, \mathbf A_2^\text{up}, \ldots, \mathbf A_L^\text{up})\in \mathbb R^{N_\text{up} \times N_\text{up}\times N_\text{up}^\text {Att}}$일 때, 이 과정을 식으로 나타내면 다음과 같다.

  1. $r_l(\mathbf A^\text {up})$: $\mathbb R^{N_\text{up} \times N_\text{up}\times N_\text{up}^\text {Att}} \rightarrow \mathbb R^{N_\text{up} \times N_\text{up}\times N^\text{H}}\rightarrow \mathbb R^{N \times N\times N^\text H}$

     • $N_\text {up}^\text {Att}$는 Head개수와 층 수를 고려해 $N^\text HL$이다.

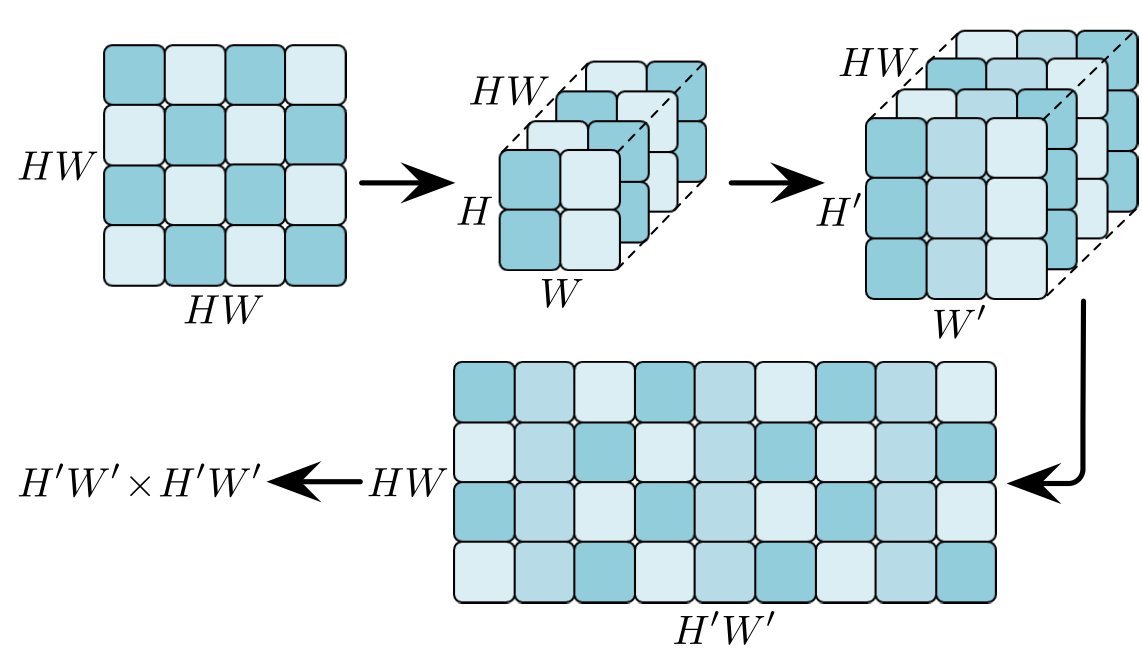
     $\mathbb R^{N_\text{up} \times N_\text{up}\times N^\text{H}}\rightarrow \mathbb R^{N \times N\times N^\text H}$의 Upsample은 Feature Reuse와 달리 $N$행과 $N$열들이 이미지 같은 위치 관계가 아닌 Attention Score로 이루어 졌으므로 단순히 Interpolation하면 안되어 저자들은 이를 고려한 Upsample을 사용했다. 아래 그림의 $HW$는 위 식의 $N_\text {up}$이고 $H’W’$는 $N$이다.

     

  2. $\text{Attention}(z_l)=\text {Softmax}(\mathbf A_l+r_l(\mathbf A^\text{up}))\mathbf V_l$

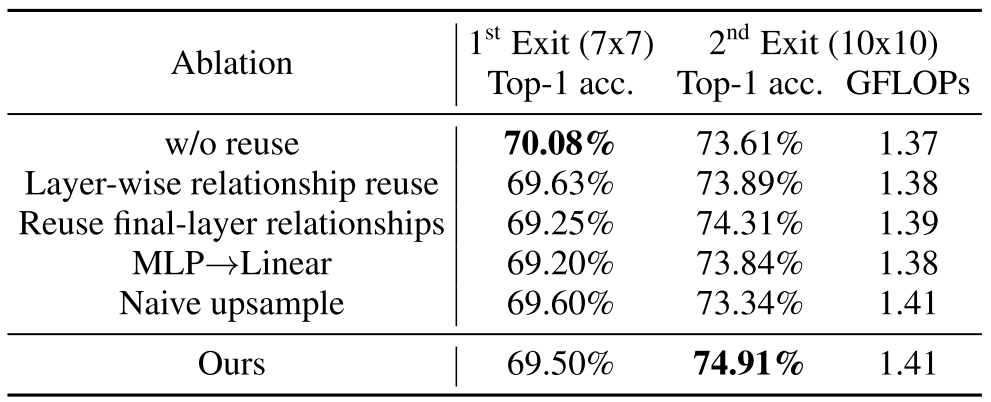
  Relationship Reuse도 Ablation이 있다. Naive upsample은 위의 Upsample을 사용하지 않은 것이다.

  

최종적으로, 각 Reuse에 따른 성능 향상은 다음과 같다.

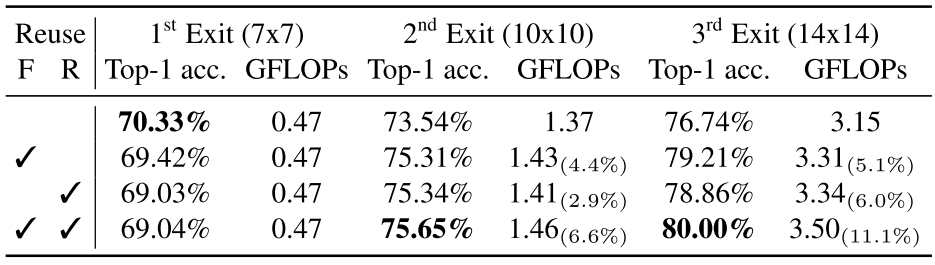
Results

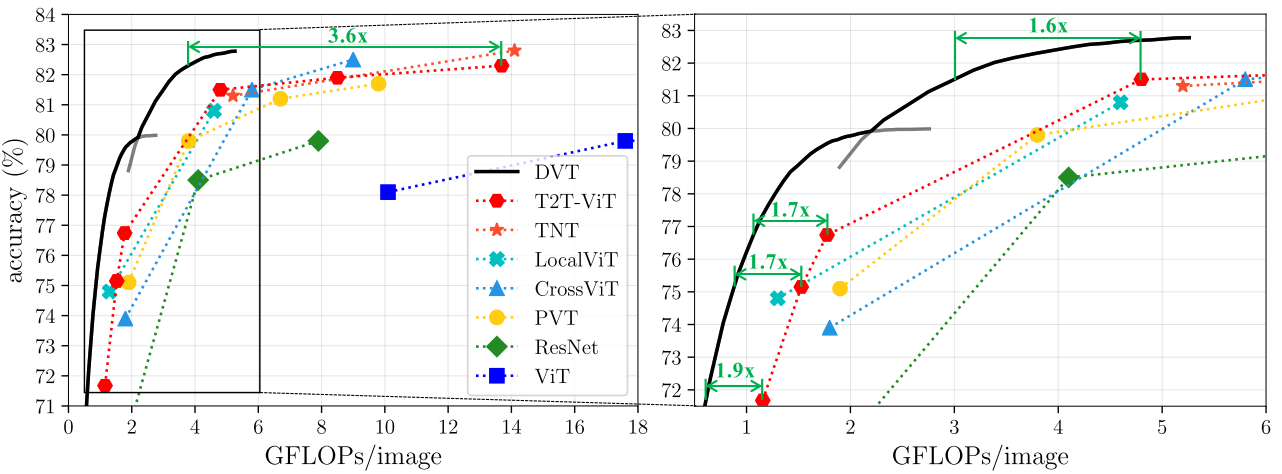
결과적으로 성능은 잃지 않으면서 Inference 속도는 훨씬 줄일 수 있었다.

Remarks

지속적으로 Transformer의 Patch 개수를 바꾸는 연구를 찾아보고 있다. 위에 정리에는 포함하지 않았는데, Dynamic Model은 CNN 계열 모델에서 이미 제안되었다고 하니 특별한 연구는 아닌 듯(이 논문과 동일 저자긴 하다). 전체적으로 저자가 이전 연구를 Navie하게 가져다 붙인 것 같다.