Sharpness-Aware Minimization for efficiently improving generalization

관련 링크 : https://arxiv.org/abs/2010.01412

• Sharpness에 따라서 Optimization하는 Sharpness Aware Optimization을 제안
• 배치의 크기가 작을수록 일반화 성능이 나아지는 경향성, $m$-$sharpness$를 발견

Intro

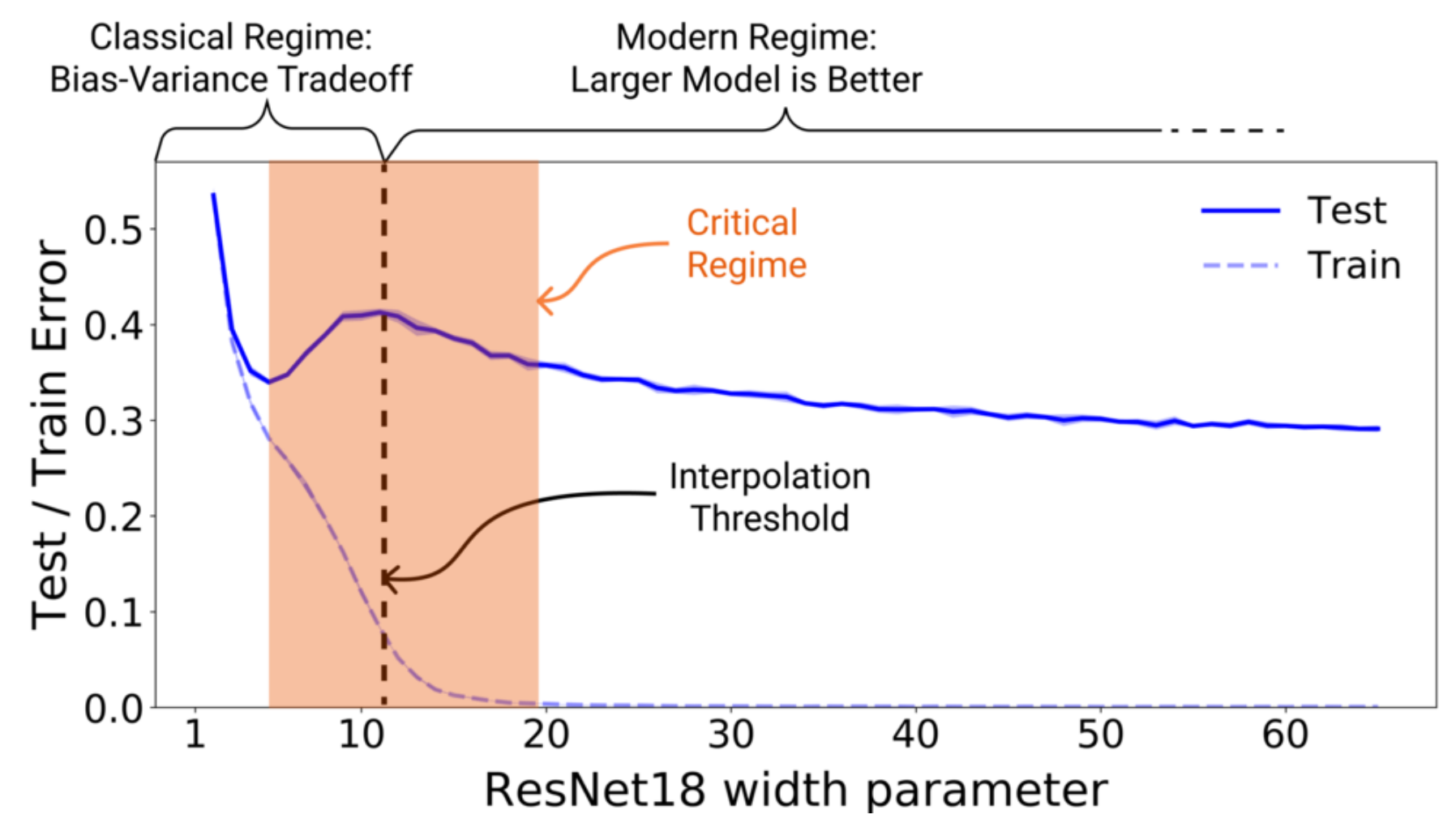
많은 분야에서 딥 러닝 모델들이 사용되고 SOTA를 달성하고 있지만, 아직까지 누구도 왜 딥 러닝 모델들이 좋은 성능을 내는지 명확히 설명할 수 없다. 머신 러닝에서 당연하게 여겨지는 Bias-Variance Trade-Off 조차 Deep Double Descent과 많은 성공한 Overparameterized 모델들을 보면 성립하지 않는다. 심지어 많은 양의 데이터가 오히려 성능을 떨어뜨리는 경우도 종종 발생한다. 따라서 많은 연구자들이 Bias-Variance Trade-Off를 대체할, 딥 러닝의 무언가와 일반화 성능간의 관계를 찾으려고 노력하고 있다.

딥 러닝에서 일반화 성능과 관련된 ‘무엇’을 논할 때 데이터의 수, 파라미터의 수 등등을 이야기 할 수 있겠지만, 보통 저런 수의 변화에 따른 Loss Landscape의 형태와 일반화 성능을 관련시킨다. 구체적으로 학습 이후의 Loss Landscape의 형태를 보고, 최종적으로 도달한 Minima가 Sharp한지 Flat한지 본 후 일반화 성능과 관련시키는 연구가 많다. 하지만 아직까지 어떤 형태의 Minima가 좋은지 명확히 답을 내릴 수는 없다. Flat Minima가 좋다는 연구도 있고, Sharp가 좋다는 연구도 있다.

오늘 소개할 논문 역시 이런 Minima의 형태와 관련된 논문으로, Flat Minima가 일반화에 더 좋다는 가정에서 출발한다. 알려진 것 처럼 Loss Landscape는 아주 복잡한 Non-Convex의 형태를 띄고 있으며 다양한 Local 혹은 Global Minima를 가지고 있다. 이는 학습 방법에 따라서 Flat Minima에 도달 할 수도, Sharp Minima에 도달 할 수도 있다는 의미다. 그럼, Minima의 형태가 Flat 하도록 학습 방법을 수정하면 더 좋은 일반화 성능을 가지지 않을까?

Loss Landscape에 영향을 주는 요소는 다양하다. 모델의 파라미터 수, 사용 할 수 있는 학습 데이터 수, 학습에 사용된 여러 기법들 등등이 모두 Landscape에 영향을 준다. 이런 요소들을 바꿔가면서 Loss Landscape를 Flat하게 만들어 애초에 Sharp Minima가 존재하지 않도록 만들면 가장 이상적일 것이다. 그런데, 이는 불가능하다. 따라서 저자들은 Loss Landscape를 건드리지 않고, 애초에 Sharp한 방향으로 학습되지 않고 Flat 한쪽으로 모델이 학습되도록 Optimizer를 수정했다. 이를 Sharpness Aware Minimization으로 줄여서 SAM이라고 한다.

SAM

그런데, Loss Landscape가 뭘까? 모델의 파라미터 $w$​​​​​​​에 따른 Loss의 Landscape를 의미한다. Landscape이므로 시각화를 해서 확인 하며, 모델의 파라미터가 고차원이므로 저차원으로 차원을 낮춰 시각화 한다. 이에 관련된 연구도 다양하지만, 간략한 설명을 위해서 $w$​​​를 2차원으로 Projection 했다고만 생각하자. 그러면 $w$​​​​​​​​에 따른 Loss의 등고선을 얻을 수 있다.

보통 시각화를 할 때는 연산량의 이유로 $w$의 범위를 작게 하지만, 모든 $w$​​​​​에 대해서 이를 그렸다고 생각해보자. Loss Landscape는 Non-Convex로 다양한 Minima들이 존재하므로 당연히 여러개의 Minima가 존재할 것이다. 저자들은 Flat Minima가 좋다고 가정하므로, Optimizer가 존재하는 여러 Minima중 Flat Minima에 도달하도록 만들면 된다.

Flat하다는 것은 Loss Landscape의 등고선이 촘촘하지 않다는 것을 말한다. 즉, 파라미터 $w$와 $w$에 약간의 노이즈를 더한 $w+\epsilon$의 Loss 차이가 작은 곳에 $w$가 도착하도록 만들어야 함을 뜻한다. 즉, Loss를 계산할 때 다음의 Sharpness도 고려하면 Optimizer가 Flat Minima로 수렴할 수 있다.

\[\text{Sharpness}=L_\mathcal S(w+\epsilon)-L_\mathcal S(w)\]

위의 식은 시각화 했을 때의 Sharpness를 말한다. 시각화로 나타나는 Sharpness가, 시각화 불가능 하지만 차원 축소 없이 Loss Landscape를 나타냈을 때의 Sharpness와는 다르다. 그래서 보통 Loss Landscape의 Sharpness를 Hessian의 고유값으로 확인한다.

• $\mathcal S$는 Training Dataset을 의미하며, 실제 데이터 분포 $\mathcal D$에서 뽑힌다. 분류 문제의 경우 식으로는 $\mathcal S \triangleq \bigcup^n_{u=1}{(\boldsymbol x_i, \boldsymbol y_i)}$​​이다.
• $L_\mathcal S$는 Training Dataset 전부를 이용해 계산한 Loss로, $L_\mathcal S(\boldsymbol w)\triangleq \frac{1}{n}\sum^n_{i=1}l(\boldsymbol w, \boldsymbol x_i, \boldsymbol y_i)$를 뜻한다.

저자들도 이를 고려해서 Optimizer가 최적화할 Loss를 다음과 같이 수정했다.

\[\begin{matrix} \text{Loss}&=&\text{Sharpness}+L_\mathcal S(\boldsymbol w) +h(\|\boldsymbol w\|^2_2/\rho^2)\hfill \\ &=& [\max_{\|\epsilon \|_2\leq \rho}L_\mathcal S(\boldsymbol w+ \boldsymbol\epsilon)-L_\mathcal S(\boldsymbol w)]+L_\mathcal S(\boldsymbol w) +h(\|\boldsymbol w\|^2_2/\rho^2)\\ &\approx& L_\mathcal S^{SAM}(\boldsymbol w) + \lambda\|\boldsymbol w\|^2_2 \hfill \end{matrix}\]

• $h: \mathbb R_+ \rightarrow \mathbb R_+$로 Strictly Increasing Function($x_1 <x_2$일 때 $f(x_1)<f(x_2)$​인 함수)이므로 간단히 근사한다.

사실 해결하려는 문제를 위처럼 단순하게 근사하기 위해 여러 정리를 이용하지만, 수식 전개가 중요한 건 아니므로 개념적으로 정리했다. 그리고 내가 이해하기 힘들기도 :(

즉, 기존 Loss를 Sharpness와 Weight Decay를 추가한 것으로 바꿔 Loss를 가장 작게하는 $w$​​​​를 찾으면 된다. 이는 미분을 통해 Gradient Descent하면 되는데, $L_\mathcal S^{SAM}(\boldsymbol w)$​​​ 내부의 $\epsilon$​​​을 모르므로 이를 First-order Taylor Expansion으로 다음과 같이 근사하고,

\[\boldsymbol e^*(\boldsymbol w)\triangleq \underset{\|\boldsymbol \epsilon \|_p\leq \rho}{\arg\max}\ L_\mathcal S(\boldsymbol w + \boldsymbol \epsilon) \approx \underset{\|\boldsymbol \epsilon \|_p\leq \rho}{\arg\max}\ L_\mathcal S(\boldsymbol w)+\boldsymbol \epsilon^T\nabla_\boldsymbol w L_\mathcal S(\boldsymbol w)=\underset{\|\boldsymbol \epsilon \|_p\leq \rho}{\arg\max}\ \boldsymbol \epsilon^T\nabla_\boldsymbol w L_\mathcal S(\boldsymbol w)\]

이 후 Dual Norm Problem을 풀어서

\[\hat{\boldsymbol \epsilon}(\boldsymbol w) = \rho\ \text{sign}(\nabla_\boldsymbol w L_\mathcal S(\boldsymbol w))|\nabla_\boldsymbol w L_\mathcal S(\boldsymbol w)|^{q-1}/\bigg(\|\nabla_\boldsymbol wL_\mathcal S(\boldsymbol w)\|^q_q\bigg )^{1/p} \tag 1\]

지식이 얕아 Dual Norm Problem을 푼다는게 무슨 말인지 모르겠다. 논문에서는 $p=2$​를 사용했고, Pytorch 코드로는 다음과 같다.

grad_norm = (parameter.grad).norm(p=2)
scale = rho/(grad_norm + 1e-12)
e_w = parameter.grad * scale.to(p)

과 같이 근사한다. 그리고 이를 이용해 최종적으로 $L_\mathcal S^{SAM}(\boldsymbol w)$​를 다음과 같이 미분하고,

\[\begin{matrix} \nabla_\boldsymbol w L_\mathcal S^{SAM}(\boldsymbol w) &\approx& \nabla_\boldsymbol w L_\mathcal S(\boldsymbol w + \hat{ \boldsymbol \epsilon}(\boldsymbol w))=\frac{d(\boldsymbol w+\hat{\boldsymbol \epsilon}(\boldsymbol w))}{d\boldsymbol w}\nabla_\boldsymbol wL_\mathcal S(\boldsymbol w)|_{\boldsymbol w + \hat {\boldsymbol \epsilon}(\boldsymbol w)} \\ &=& \nabla_\boldsymbol wL_\mathcal S(\boldsymbol w)|_{\boldsymbol w + \hat {\boldsymbol \epsilon}(\boldsymbol w)}+ \frac{d\hat{\boldsymbol \epsilon}(\boldsymbol w)}{d\boldsymbol w}\nabla_\boldsymbol wL_\mathcal S(\boldsymbol w)|_{\boldsymbol w + \hat {\boldsymbol \epsilon}(\boldsymbol w)} \hfill\\ &\approx & \nabla_\boldsymbol w L_\mathcal S(\boldsymbol w)|_{\boldsymbol w + \hat {\boldsymbol \epsilon}(\boldsymbol w)} \hfill \end{matrix} \tag 2\]

두 번째 줄의 두 번째 항은 $\hat{\boldsymbol \epsilon}(\boldsymbol w)$가 $\nabla_\boldsymbol w L_\mathcal S(\boldsymbol w)$​의 함수이므로 Hessian이 된다. 이는 쉽게 계산 할 수 있지만, 결과에 큰 차이가 없으므로 생략해서 사용한다. 자세히 말하면, 실험을 통해 확인한 결과 학습의 초기 절반 동안은 Fisrt Order와 Second Order 근사가 Cos 유사도가 1에 가깝고, 모델이 수렴에 가까워지면 달라진다. 다행히 Second Order를 생략한 모델이 더 성능이 높았다. 하지만 그 이유는 모호하므로 추가 연구가 필요해 보인다.

이를 이용해 파라미터를 업데이트한다. 전체 과정을 요약하면 다음과 같다.

1. 한 배치 $\mathcal B$를 이용해 첫 번째 Forward, Backward를 계산하고, 식 (1)을 이용해 $\hat {\boldsymbol \epsilon}(\boldsymbol w)$를 근사한다.
2. 위에서 구한 $\hat {\boldsymbol \epsilon}(\boldsymbol w)$​를 파라미터에 더해 두 번째 Forward, Backward를 계산하고, 식 (2)를 이용해 $\nabla_\boldsymbol w L_\mathcal B^{SAM}(\boldsymbol w)$​를 근사한다.
3. 파라미터에 $\hat {\boldsymbol \epsilon}(\boldsymbol w)$을 뺀 후, $\nabla_\boldsymbol w L_\mathcal B^{SAM}(\boldsymbol w)$​​를 이용해 파라미터를 업데이트한다.

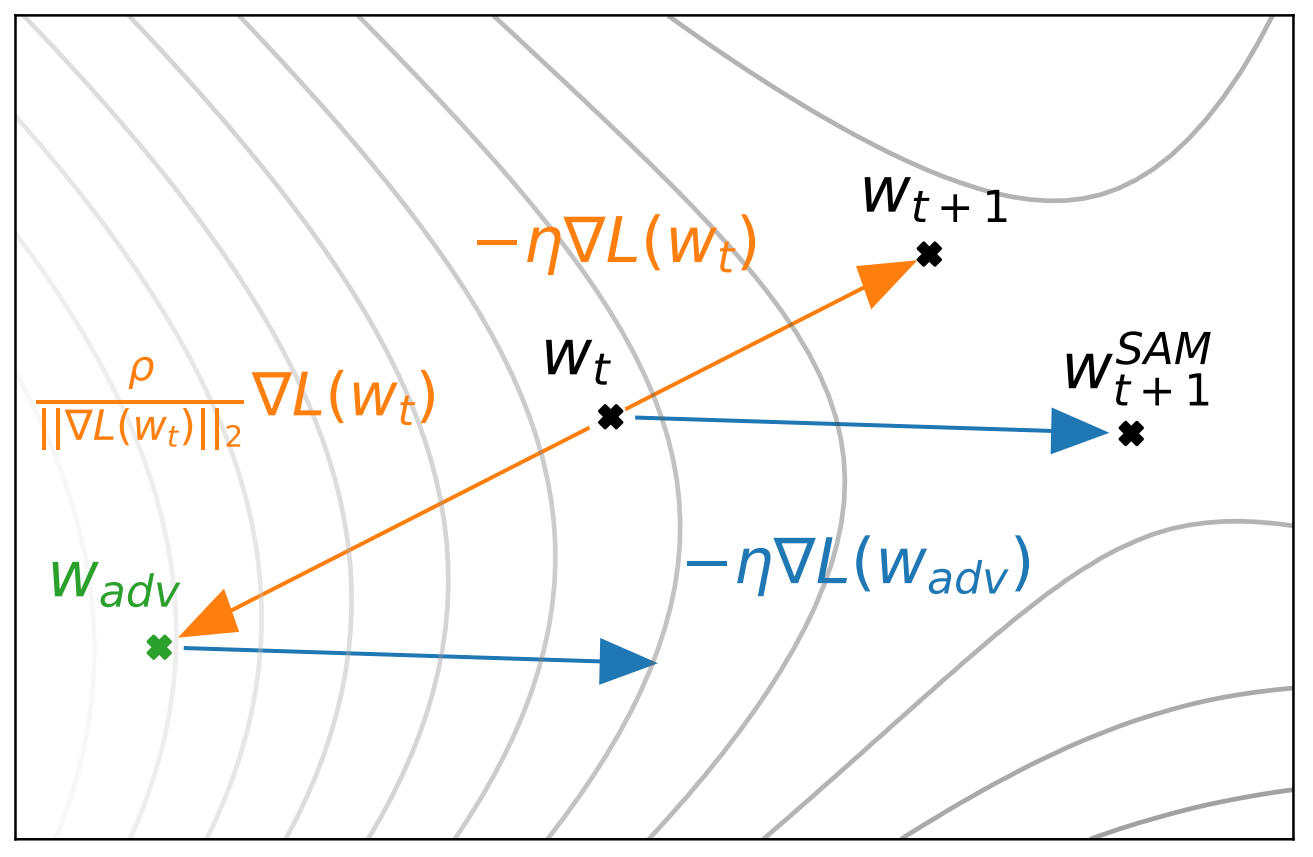
SAM을 이용한 파라미터의 움직임을 나타낸 것. $\text W_{t+1}^\text{SAM}$이 SAM을 이용했을 때 업데이트된 파라미터의 위치를 나타냄. $\hat {\boldsymbol \epsilon}(\boldsymbol w)$는 Grad를 이용해서 계산되므로 Adversarial한 방향과 동일해 위 그림에서 $w+\epsilon$을 $\text W_\text{adv}$​로 표현함.

그런데 위에서 적은 SAM의 진행 과정과 식 (2)를 자세히 살펴보면, 하나 다른 점이 있다. 식 (2)는 Training Set $\mathcal S$에 대한 식이고, 진행 과정은 배치 $\mathcal B$에 대한 것이다. 이는 구현상의 이유로 바뀐 것으로 큰 차이를 가져오진 않는다. 차이는 $\mathcal S$에 대해서 $\hat {\boldsymbol \epsilon}(\boldsymbol w)$을 구하는게 아니고 각 $\mathcal B$에 대해 $\hat {\boldsymbol \epsilon}(\boldsymbol w)$를 구하는 것으로, 각 $\mathcal B$마다 독립적인 $\hat {\boldsymbol \epsilon}(\boldsymbol w)$​에 대해 SAM을 수행하는 것과 같다. 하나 재밌는 점은 $\mathcal B$의 크기인 $m$​에 따라서 일반화 성능이 달라진다는 것이다.

논문에 배치 크기가 작을수록 Mutual Information이 높음을 나타내는 그래프도 있다. 하지만 그 그래프와 일반화 성능의 관계를 유추하기가 어려워 첨부하진 않았다.

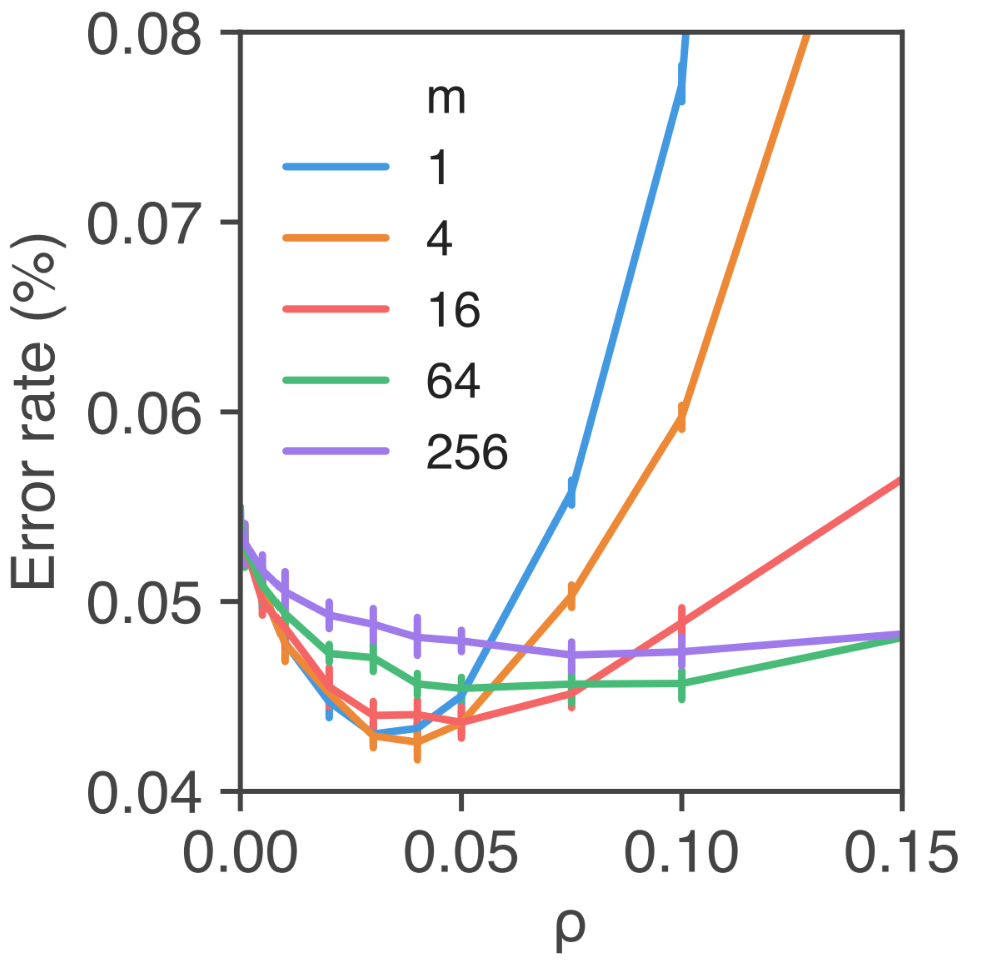
위의 그림을 보면, 낮은 $m$​이 더 낮은 Error rate를 가지는 것을 볼 수 있다.

낮은 $m$이 알려진 것처럼 Stochasticity를 높여서 혹은 낮은 $m$에서 파라미터 업데이트 횟수가 잦아져 기본적으로 SAM에 걸려있는 Weight Decay 때문에 Loss Landscape가 Smooth 해지기 때문이지 않을까?

Empirical Evaluation

여러 실험이 있지만, 기존 방법들 보다 성능이 더 좋더라 같은 실험은 제외하고 알아둘만한 실험만 정리하겠다.

1. Training Epoch이 늘어 날수록 성능이 늘어나는 경향이 있음

   

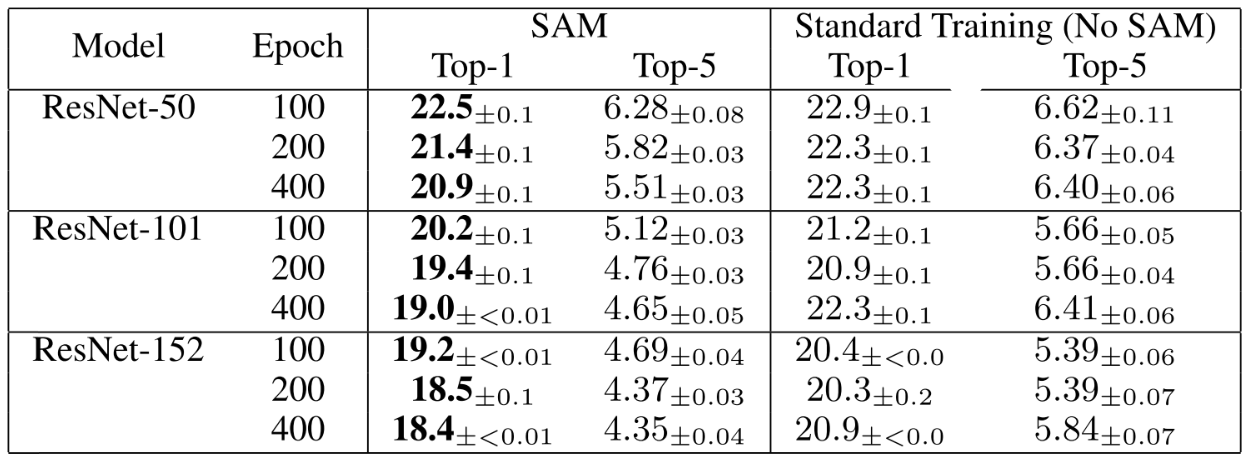
   SAM은 한 번의 파라미터 업데이트를 위해 두 번의 Forward/Backward를 요구한다. 따라서, 100 Epoch 학습한 SAM과 Non-SAM을 비교하기 위해 Non-SAM의 경우 100 Epoch과 200 Epoch 중 더 성능이 좋은 것으로 기록했다.

2. SAM을 사용한 것만으로 Label noise robustness를 개선하는 이전 연구들보다 나은 성능을 보임

   

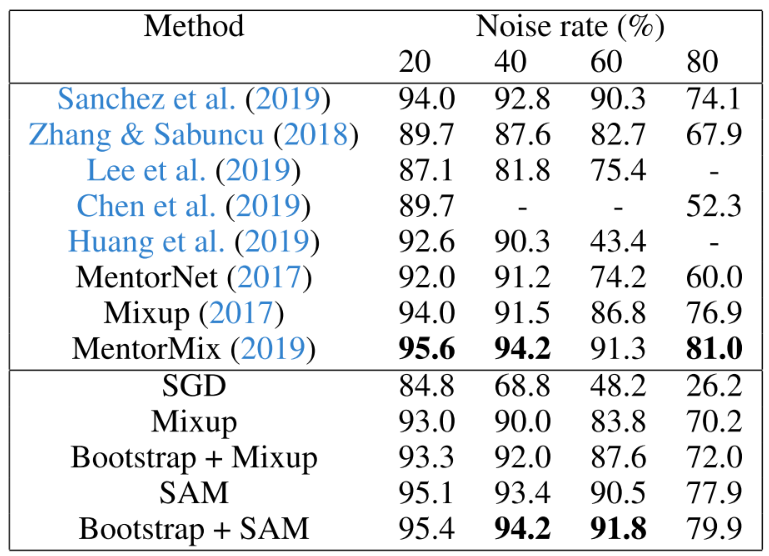
   Noise가 있는 CIFAR-10 Training Set을 이용해 Clean Test Set에서의 성능을 측정. 각 성능은 해당 논문에서 가져옴

Sharpness and Generalization through the Lens of SAM

성능 향상은 확인 했으므로, 성능 향상이 SAM이 의도한 것 처럼 Flat Minima로 인한 것인지 확인 해보자. 2차원으로 차원을 줄여 시각화 한 것으로도 경향성은 판단할 수 있지만 정확하지 않으므로, Epoch에 따른 Hessian의 고유값 분포를 이용해 확인한다.

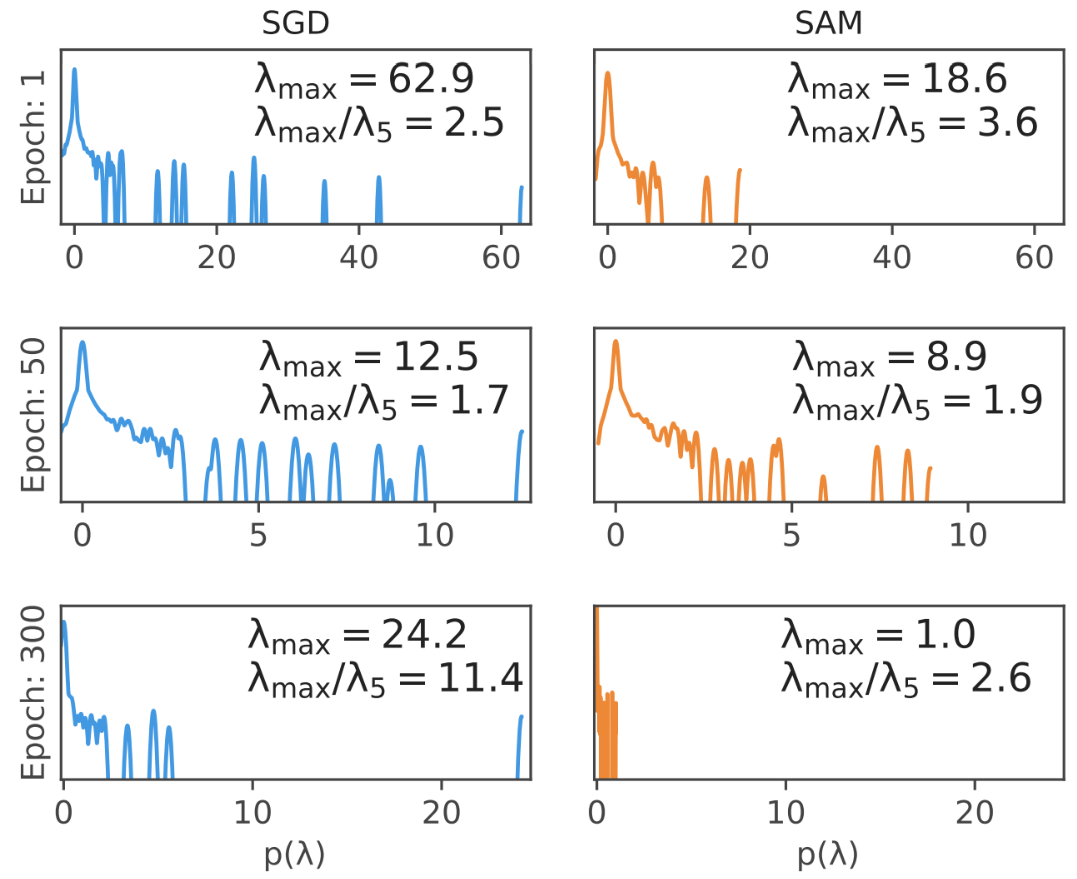
SAM을 이용한 경우 그렇지 않은 경우보다 곡률이 낮고 $\lambda_\text{max}$​​​​​의 최대값도 낮아짐을 알 수 있다. 이는 SAM이 의도한대로 Flat해짐을 보여준다.

Remarks

나름 재밌는 논문이긴 한데 SAM이 모델에 미치는 영향에 대한 분석이 약간 빈약한 느낌이다. 후속 연구 나오면 살펴 봐야 할듯