Visualizing the Loss Landscape of Neural Nets

관련 링크 : https://arxiv.org/abs/1712.09913

• Filterwise-Normalization을 이용해 더 설득력 있는 Loss Landscape 시각화를 수행
• 시각화를 통해 Sharpness와 Generalization Gap 사이의 상관 관계를 보임
• PCA를 이용해 Loss Landscape에서 최적화 경로를 시각화 하는 방법을 제안

Intro

인공신경망을 학습시키기 위해서는 Loss를 최소화 해야 한다. Loss는 고차원의 Non-convex 함수이고 이론적으로 이를 최소화하는 경로를 찾기는 힘들다. 그러나, 놀랍게도 실제 Deep Learning 방법들은 간단한 Gradient Descent 방식으로 Global Minima를 찾는다. 문제는 이렇게 Global Minima를 찾는 경우가 흔하지 않다는 점이다.

모델이 Global Minima로 수렴할 수 있을지 아닐지는 모델의 구조, 사용된 Optimizer, 파라미터 초기화 방식에 따라 달라진다. 따라서 간단히 어떤 구조가 좋고, 어떤 Optimizer가 적절하며 어떤 파라미터 초기화 방식이 최적인지를 안다면, Global Minima를 찾기 쉬울 것이다. 문제는 각 선택들이 모델에 어떤 영향을 주었는지 개별적으로 알기 어렵다는 점이다. 모델의 성능은 각 선택들이 준 복합적인 영향의 결과이므로 개별 요소들의 영향을 알기 쉽지 않다. 실험적으로 알아 내려 한다고 해도, 이는 어마어마한 연산량을 요구한다. 그래서 Loss Surface를 시각화해 여러 변화에 따른 특성을 실험적으로 분석하는게 도움이 된다.

어떤식으로 도움이 되는지 궁금하다면, Loss Surface의 Flatness 혹은 Sharpness가 Generalization Gap에 어떤 영향을 미치는지에 관한 다양한 연구들을 살펴보면 좋을 것 같다. 물론 아무 영향도 없다는 연구도 있다.

오늘 리뷰할 논문은 이런 실험적 분석을 위한 Loss Surface 시각화에 관련된 논문이다.

Basics of Loss Function Visualization

Loss Function을 시각화 한다는 것은 어떤 의미일까? 모델을 학습시키면서 가장 많이 보게되는 Training Curve역시 Loss Function의 시각화이다. Training Curve는 Epoch 혹은 Iteration에 따른 Loss Function의 시각화이고, Training Curve를 분석해 Optimizer의 수렴 속도, 모델의 구조에 따른 수렴 속도 등에 관한 통찰을 얻을 수 있다.

하지만 오늘의 논문에서 말하는 시각화는 학습 횟수가 아닌 파라미터에 따른 시각화이다. 따라서, 먼저 기존 방식들을 살펴보자.

1-Dimensional Linear Interpolation

초기 파라미터 $\theta$​에서 학습으로 얻어진 파라미터 $\theta’$​까지의 Loss를 시각화 하려면 어떻게 해야될까? 당연히 가로 축은 $\theta$​의 변화량이고 세로 축은 Loss인 그래프를 그리면 된다. 하지만, $\theta$​​​​는 고차원 벡터이므로, 수선(1차원)에 표현 할 수 없다. 따라서 차원을 줄여 $\alpha$​라는 스칼라 값으로 이를 표현한다.

\[\theta(\alpha)=(1-\alpha)\theta+\alpha\theta'\]

그리고 이를 이용해 Loss Fucntion

\[f(\alpha)=L(\theta(\alpha))\]

를 시각화 한다.

관련 연구로 이 방식을 응용해서 초기 파라미터와 서로 다른 두 Optimizer로 얻은 파라미터들 간의 Loss Surface를 표현하기 위해 Barycentric Interpolation을 이용하거나, 네 가지 파라미터를 비교하기 위해 Bilinear Interpolation을 사용했다.

Contour Plots & Random Directions

모델의 파라미터를 $\theta=(a, b)$​​​​와 같이 좌표로 나타낼 수 있다면 1-D Linear Interpolation은 두 좌표 사이의 직선을 가로 축으로 Loss Function을 시각화 한 것이다. 하지만 직선보다는 좌표 평면에 따른 Loss를 시각화 하는게 더 Loss Surface의 특징을 보기에는 좋을 것이다. 따라서 Loss Surface를 Contour Plot으로 그리는 방법이 있다.

Contour Plot은 지도에서 높이에 따라 등고선으로 선을 긋는 등고선도를 의미한다. 등고선으로 Loss의 값을 표현하므로 앞선 1-D Linear와 다르게 세로 축도 조작 변인이 된다.

등고선도에서 위도와 경도로 표현되는 좌표에 따른 고도를 표현 하듯 Loss Surface의 Contour Plot에도 위도와 경도, 그리고 좌표가 필요하다. 그래서 위도와 경도의 역할을 수행할 벡터 $\delta$​와 $\eta$​를 무작위로 뽑고, 스칼라 $\alpha$​와 $\beta$​​를 이용해 좌표를 다음과 같이 표현한다.

\[\theta(\alpha, \beta) = \theta^*+\alpha \delta+\beta\eta\]

$\theta^*$는 중심 파라미터로, 시각화 하고자 하는 중심점을 의미한다. 위도와 경도는 직교하는데 $\delta$와 $\eta$​는 Guassian 분포에서 무작위로 뽑으니 직교하지 않으므로

그리고 1-D Linear와 동일하게 $f(\alpha, \beta)=L(\theta(\alpha,\beta))$를 시각화 한다.

Filter-Wise Normalization

앞서 설명한 방식들로 손쉽게 Loss Landscape를 그릴 수 있게 되었다. 하지만, 이 방식들은 시각화의 목적인 여러 선택들에 따른 영향을 공정하게 비교할 수 없다. 왜냐하면, ReLU 같은 특정 범위의 값을 그대로 내뱉은 비선형 함수가 가지는 Scale Invariance를 고려하지 않았기 때문이다.

모델의 첫 번째 Conv의 파라미터에 10을 곱하고, 두 번째 Conv 파라미터에 10을 나눠보자. 조작을 가하기 이전의 모델과 출력은 동일한데, 파라미터의 Scale은 달라졌다. 이를 Scale Invariance라 하고, 당연하게도 각 층의 출력을 새로 Normalization하는 Batch Normalization을 사용해도 이 경향성이 나타난다.

근데, Scale Invariance를 왜 고려해야 할까? 이를 위해서 파라미터들의 값 평균이 1보다 상당히 큰 모델 A와, 1보다 상당히 작은 모델 B를 생각해보자. 두 모델은 Scale Invariant하다. 각 모델의 Loss Landscape를 시각화 하기 위해서는 방향 벡터를 이용해 파라미터에 변화를 주어야 하고, 두 모델을 비교하기 위해서는 동일한 방향 벡터를 사용할 것이다. 그런데, 모델 A는 작은 단위의 파라미터 변화가 발생해도 애초에 값들이 1보다 상당히 크기 때문에 출력에 변화가 적다. 하지만 모델 B는 출력에 큰 변화가 발생한다. 즉, 방향벡터의 크기에 따른 영향이 각 모델에게 매우 다르게 나타나므로 시각화를 통한 비교가 어려워진다.

따라서, 방향벡터의 크기에 따른 영향이 각 모델에 동일하도록 만들 필요가 있고, 이를 위해서 Filter-wise Normalized Direction을 사용한다.

\[d_{i, j} \leftarrow \frac{d_{i, j}}{\|d_{i, j}\|}\|\theta_{i, j}\|\]

• $d_{i, j}$: $i$​​번째 층의 $j$​​​번째 파라미터에 해당하는 방향 벡터. 무작위 방향에서 추출한다.

  Random Direction이라서 Direction에 따라 전혀 다른 다양한 Plot이 나오지 않냐는 의문이 들 수 있다. Appendix에서 서로 다른 여러 Direction들을 이용한 Plot들 간의 비교를 수행하는데, 1D의 경우 거의 비슷한 Plot들을 내뱉고 2D의 경우도 모양은 다르지만 동일한 특징들을 가진 Plot들이 나타남을 보여준다.

• $\theta_{i, j}$: $i$번째 층의 $j$번째 Conv 필터. FC도 1x1 Conv로 보면 동일하게 적용할 수 있다.

• $\|\cdot\|$: Frobenius Norm, Element-wise L2 norm

여기까지 이야기 해도 여전히 Filter-wise Normalization의 필요성이 느껴지지 않을 수 있다. 그래서 이번엔 기존 방법과 제안된 방법을 Sharp vs. Flat Dilemma에 적용해 비교해 보겠다.

The Sharp vs Flat Dilemma

Loss Surface를 통한 실험적 분석 중 가장 잘 알려진 것은 Small Batch SGD가 일반화가 좋은 Flat Minimizer이고 Large Batch SGD는 일반화가 상대적으로 나쁜 Sharp Minimizer라는 Dilemma이다. 이후 연구들에 의해 일반화와 Loss의 곡률은 무관하고, Large Batch에서 좋은 성능을 내는 방법들도 제안되면서 논란의 여지가 있긴 하지만, 가장 많이 연구 되었으므로 살펴보자.

비교를 위한 모델로는 9층의 VGG-BN을 사용하고 데이터 셋으로 CIFAR-10을 사용했다. Batch의 크기에 따른 모델의 파라미터를 각 $\theta^s$​, $\theta^l$​​이라 하고, 먼저 예전 방식의 1-D Linear Interpolation부터 살펴보자.

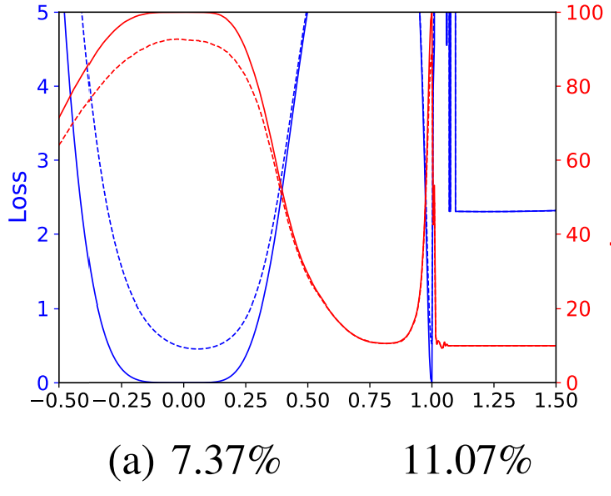
파란 선은 Loss, 빨간 선은 Acc이다. 실선은 Training, 점선은 Test에서의 결과를 나타낸다. Linear Interpolation이므로, $\theta(\alpha)=\theta^s+\alpha(\theta^l-\theta^s)$​​이다. 아래 숫자는 Test Error를 나타낸다.

시각화를 확인해 보니, 앞서 말한 것 처럼 $\theta^s$​​가 더 Flat Minima로 수렴했고 일반화 성능도 더 높게 나온다. 하지만, 여기에 Weight Decay를 적용해 보자.

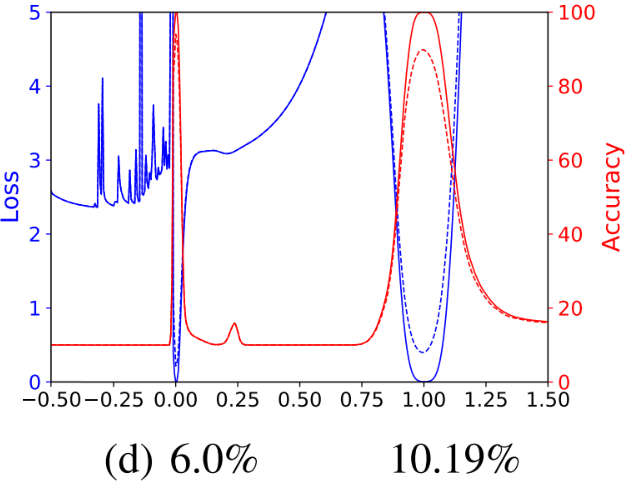
놀랍게도 $\theta^s$​​​​​가 더 날카로운 Minima로 수렴했는데, 일반화 성능은 여전히 더 좋다. 즉, 이 기존 시각화를 통한 비교로는 Sharpness와 Generalization Gap 사이의 차이를 설명 할 수 없다. 앞서 설명한 것처럼 이는 Scale Invariance를 고려하지 않았기 때문이다. 실제로 이것 때문인지 어떻게 알 수 있을까? 이는 파라미터를 살펴보면 알 수 있다.

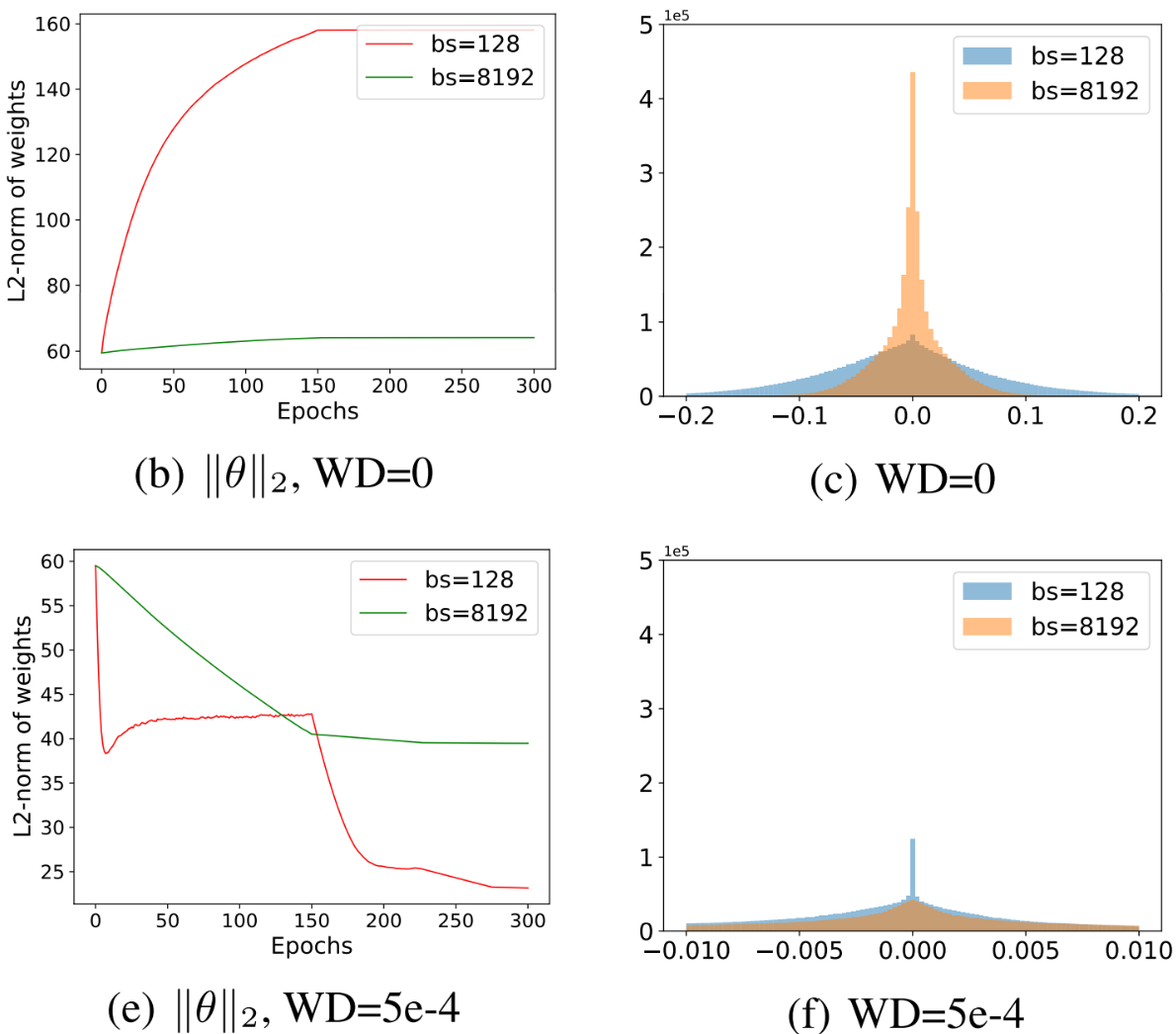
학습이 진행됨에 따라, WD를 적용하지 않았을 때 $\|\theta^s\|_2$는 커지는 반면, $\|\theta^l\|_2$은 상대적으로 매우 작다. 하지만 이 경향은 WD가 적용되면 반대로 나타난다. 이는 Small Batch SGD가 더 자주 업데이트 하므로 WD가 없을 때는 더 큰 값을 가지고 WD가 있을 때는 더 작은 값을 가지기 때문이다.

여기서 Scale Invariance의 영향을 생각해 보자. 앞서 언급했듯, Scale Invariance를 고려하지 않으면 방향벡터의 크기에 따른 영향이 각 모델에게 매우 다르게 나타난다. 위의 예시에서 WD가 없을 때 $\|\theta^s\|_2$​​​가 커서 $\alpha$​​​에 따른 영향이 작아져 Flat Minima에 수렴했고, WD가 있을 때는 반대로 $\|\theta^s\|_2$​​​가 작아 Sharp Minima에 도달했다. 이는 파라미터 크기에 따라 방향 벡터 $\theta^l-\theta^s$​의 적용 정도 $\alpha$​​​의 값이 다른 결과를 불러 일으킨 것이므로 Scale Invariance의 영향이다.

이번에는 저자들이 제안한 방법으로 시각화 해보자.

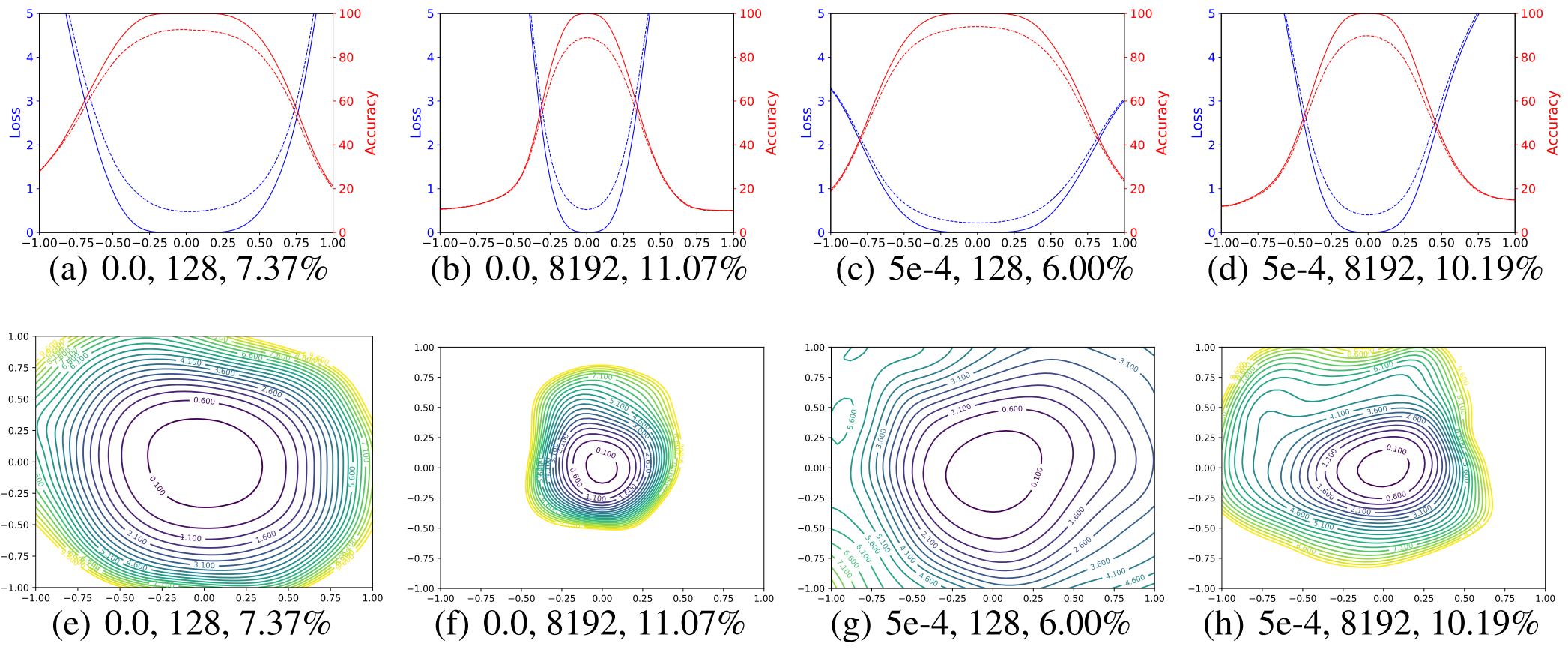
파란 선은 Loss, 빨간 선은 Acc이다. 실선은 Training, 점선은 Test에서의 결과를 나타낸다. 아래 숫자들은 Weight Decay, Batch Size, Test Error를 나타낸다.

Large Batch가 일관되게 더 Sharp한 경향성을 보이며 그 경향성이 약해졌다. 또 WD를 주었을 때 더 Flat해 졌지만 이전처럼 WD 적용 여부에 의해 일관성이 역전되지는 않았고, 모든 더 Flat한 모델들이 더 좋은 성능을 보인다. 즉, 제안한 방법을 이용하면 시각화의 결과가 일관되게 바뀌므로 방법들 간의 비교가 가능해진다.

Are we really seeing convexity?

근데, 이런 시각화를 통해 Convex 혹은 Non-Convex의 존재를 확인 하는게 믿을만 할까? 파라미터 $\theta$는 엄청나게 고차원인데, 우리는 이를 극도로 줄여 이차원으로 시각화 했으니 당연히 의문을 품을 수 밖에 없다. 따라서, 신뢰성을 검증할 필요가 있다. 보통 Loss Function의 Convexity 정도를 측정하는 방법으로 Hessian의 고유값들인 Principle Curvatures를 계산한다.

다행히 Reduced Plot($\alpha, \beta$​로 2차원)의 Principle Curvature가 Full-dimensional Surface($\theta$​​​​)의 Principle Curvature의 가중 평균임을 알 수 있으므로, 계산해 보지 않아도 시각화 도표에 Non-Convexity가 존재하면 실제 Loss Surface에도 존재함을 알 수 있다. 물론 이게 시각화의 Convex라고 무조건 고차원도 Convex임을 뜻하진 않지만 유용하다.

Hessian의 모든 고유값이 양수이면 Convex, 음수이면 Non-Convex이다. 평균값이 음수라는 것은 전체의 합이 음수임을 의미하므로 Non-Convex임을 뜻하지만, 평균이 양수라고 음의 값을 가지는 고유값이 하나도 없음을 의미하지 않기 때문에 위와 같은 결론을 도출 할 수 있다.

하지만 여전히 시각화는 저차원에서 수행하므로, 잡아내지 못하는 Non-Convexity가 존재 할 수도 있다. 그래서 파라미터 Hessian의 최소, 최대 고유값 $\lambda_{min}$​과 $\lambda_{max}$를 계산해 $|\lambda_{min}/\lambda_{max}|$를 시각화 했다.

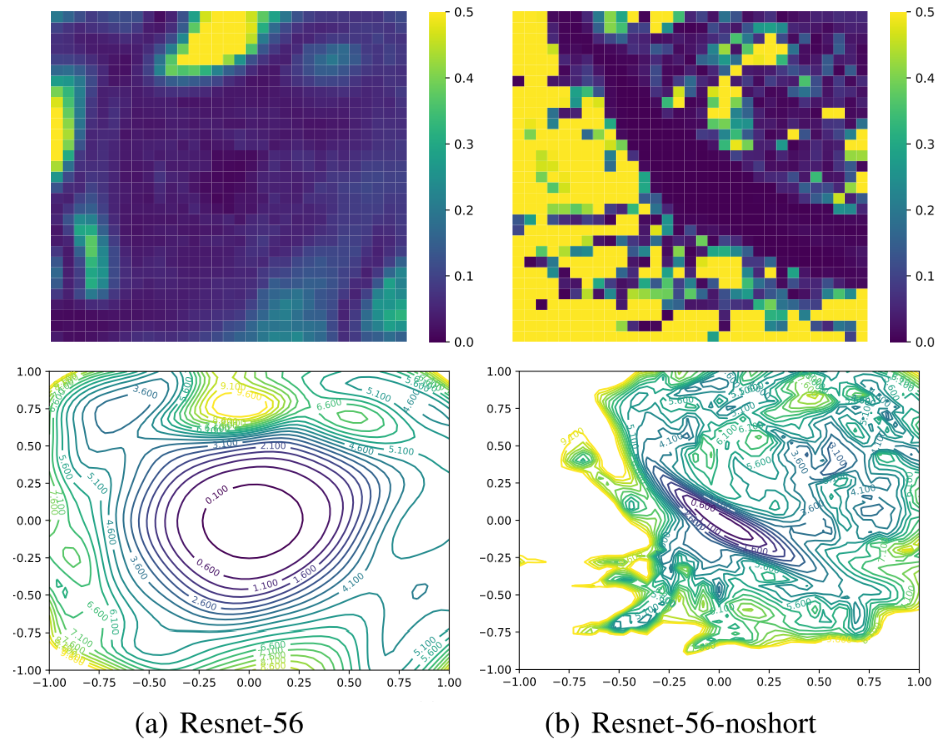
간단히 푸른색은 Convex, 노란색은 Non-Convex를 나타낸다고 볼 수 있다. noshort는 Skip Connection을 사용하지 않은 ResNet을 의미한다.

저자들이 사용한 시각화 방식이 두드러진 Non-Convex를 다 잡아내는 것을 볼 수 있다.

Analysis using Filter-Normalized Visualization

이제 공정한 시각화 방식을 찾았으니, 여러 조건에 따른 Loss Landscape를 시각화해보고 특징들을 비교, 분석해 보자. 먼저 ResNet과 Skip Connection이 없는 ResNet을 비교해보자.

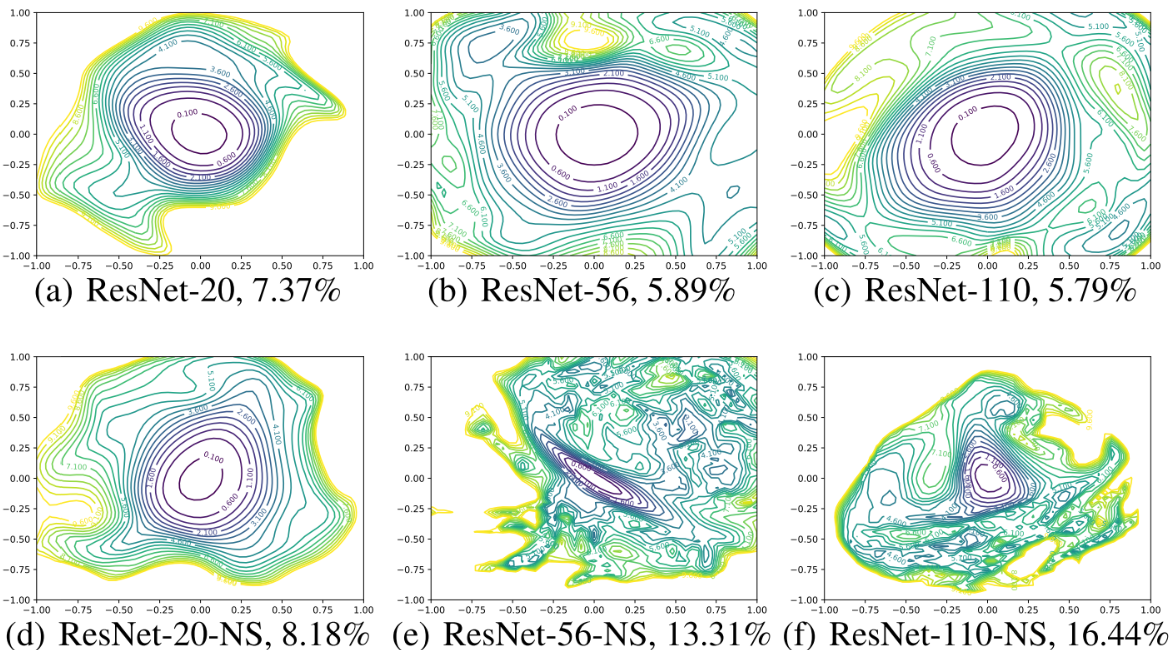
• Skip Connection이 없으면 네트워크의 층 수가 깊어질수록 Non-convexity로 이동
• Skip Connection이 없는 Deep 모델들은 Shap Minima로 수렴
• Skip Connection를 사용하면 이런 경향이 많이 해소됨

다음으로 Skip Connection 유무와 Wide한 정도에 따른 Loss Landscape를 시각화해보자.

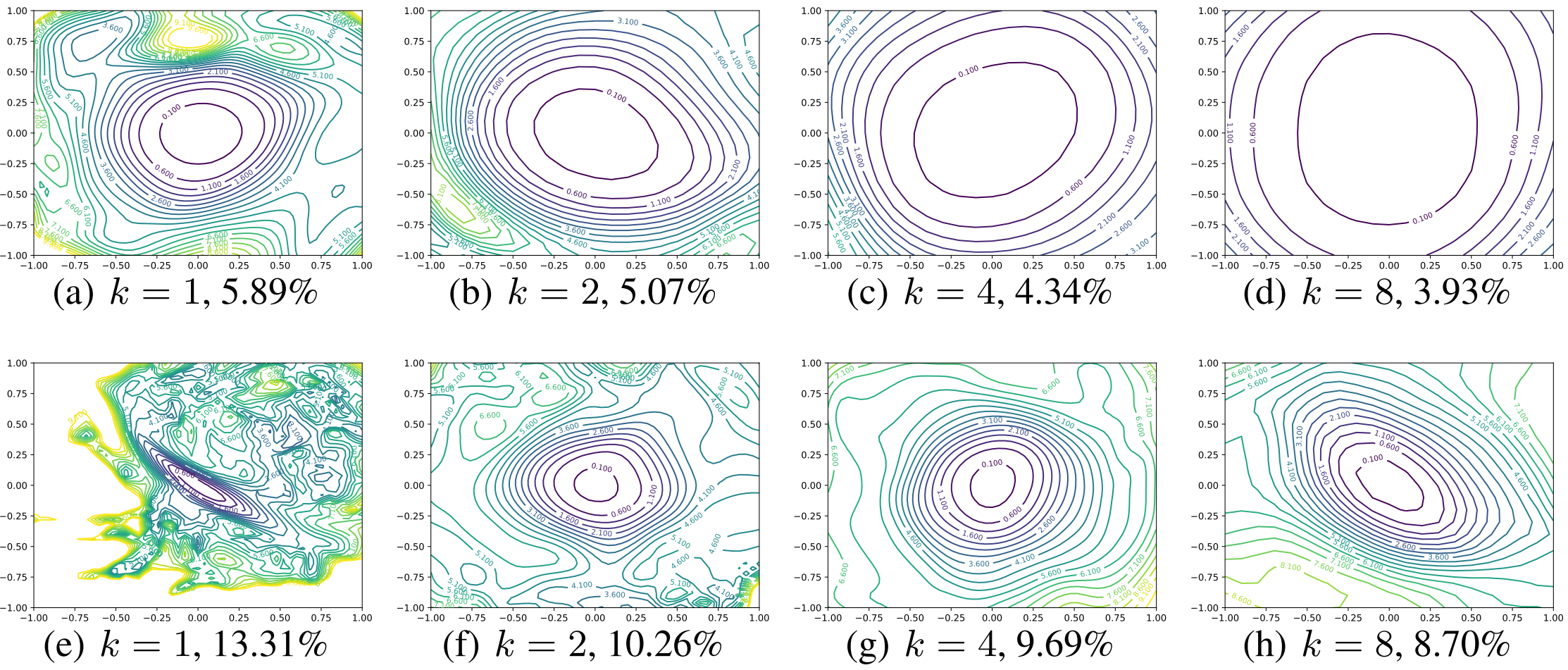
기본 모델은 ResNet-56으로 $k$​는 층당 필터 개수를 의미한다. 첫 행은 Skip Connection을 사용한 모델, 두 번째 행은 사용하지 않은 모델이다.

• 모델을 Wide하게 만들면 Loss Landscape가 Flat 해짐

위의 두 결과를 종합적으로 비교해 보면, 다음의 결론을 얻을 수 있다.

• Sharpness가 강하면 Test Error가 높음
• Convexity와 Non-Convexity의 구분이 뚜렷한 Landscape를 가진 모델들은 어떤 초기화에도 학습이 잘 됨. 그렇지 않은 녀석들은 학습이 안됨.(ResNet-156-no short는 학습이 불가능)
• 공통적으로 Flat한 녀석들이 더 좋은 일반화 성능을 보임

Visualizing Optimizaition Paths

이번에는 Loss Landscap와 동시에 최적화 경로를 시각화 해보자.

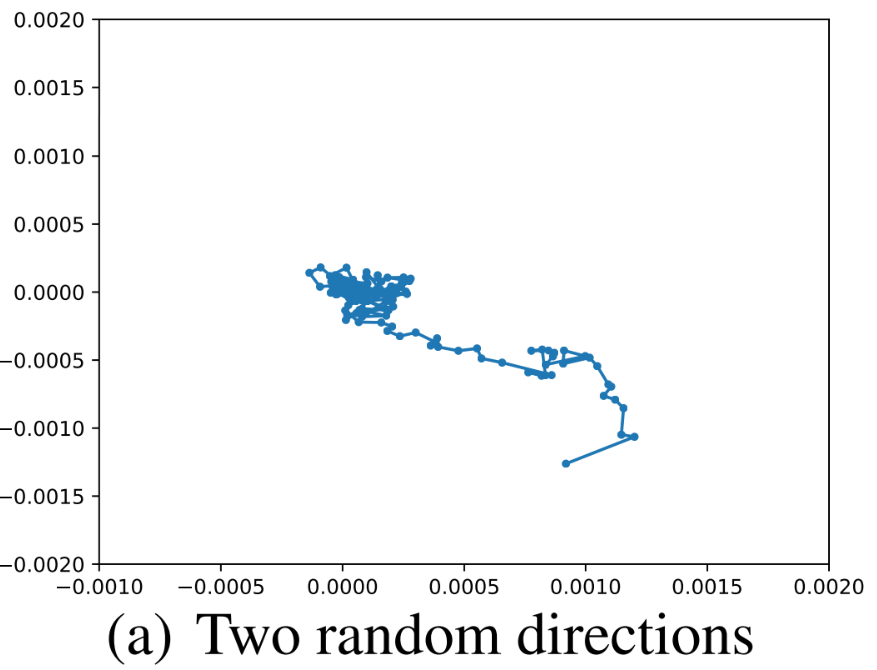
보이는 것과 같이 거의 움직이지 않는다. 이는 고차원을 저차원에 시각화하는 것이므로, Random Direction을 이용하면 변화량을 잡아내지 못하기 때문으로 보인다.

고차원에서 랜덤 벡터 두 개를 뽑으면, 차원이 높아질 수록 Orthogonal하다. 따라서 이 벡터들을 이용해 저차원에서 시각화해도 이들이 Orthogonal 하기 때문에 한 축으로는 거의 움직임을 잡을 수 없다.

그럼, 한 축은 최적화 경로로 다른 한 축은 무작위로 뽑아서 새로 시각화 해보자.

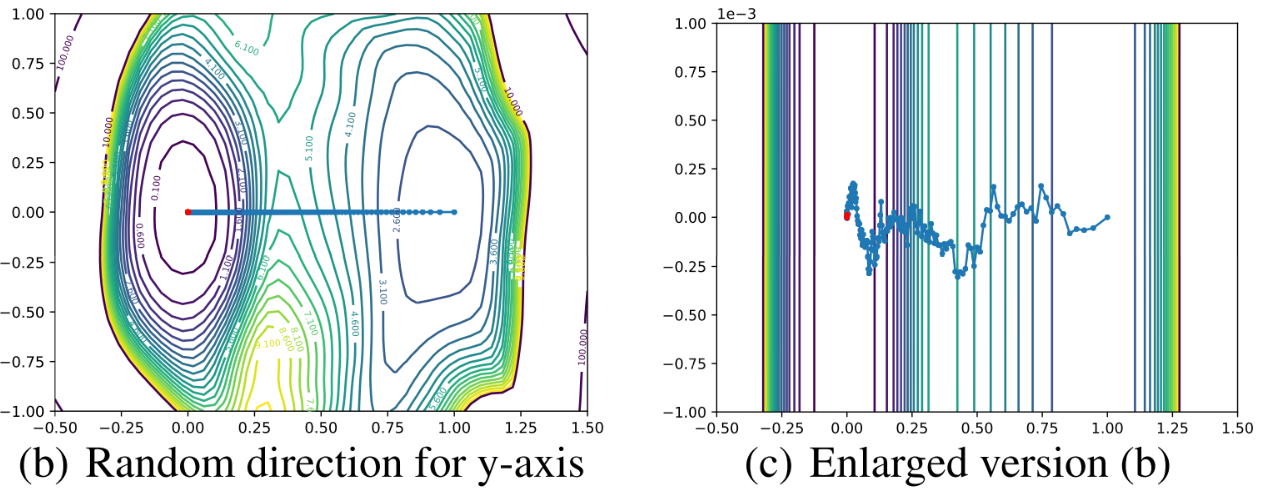
여전히 y축으로는 변화를 잡아내지 못한다. 따라서 Optimization Path를 시각화 하려면 방향 선택에 신중을 다해야 함을 알 수 있다. 저자들은 이를 위해서 PCA를 이용한다.

Effective Trajectory Plotting using PCA Directions

에폭 $i$에서 파라미터를 $\theta_i$라 하면, $n$ 에폭동안 학습 시켰을 때 $\theta_0, \ldots, \theta_n$을 얻을 수 있다. 저자들은 이를 이용해 행렬 $M=[\theta_0-\theta_n;\cdots;\theta_{n-1}-\theta_n;]$​​를 만들고,​ 이 행렬에 대해 주성분 두 개를 뽑아 시각화했다. 그 결과를 한 번 살펴보자.

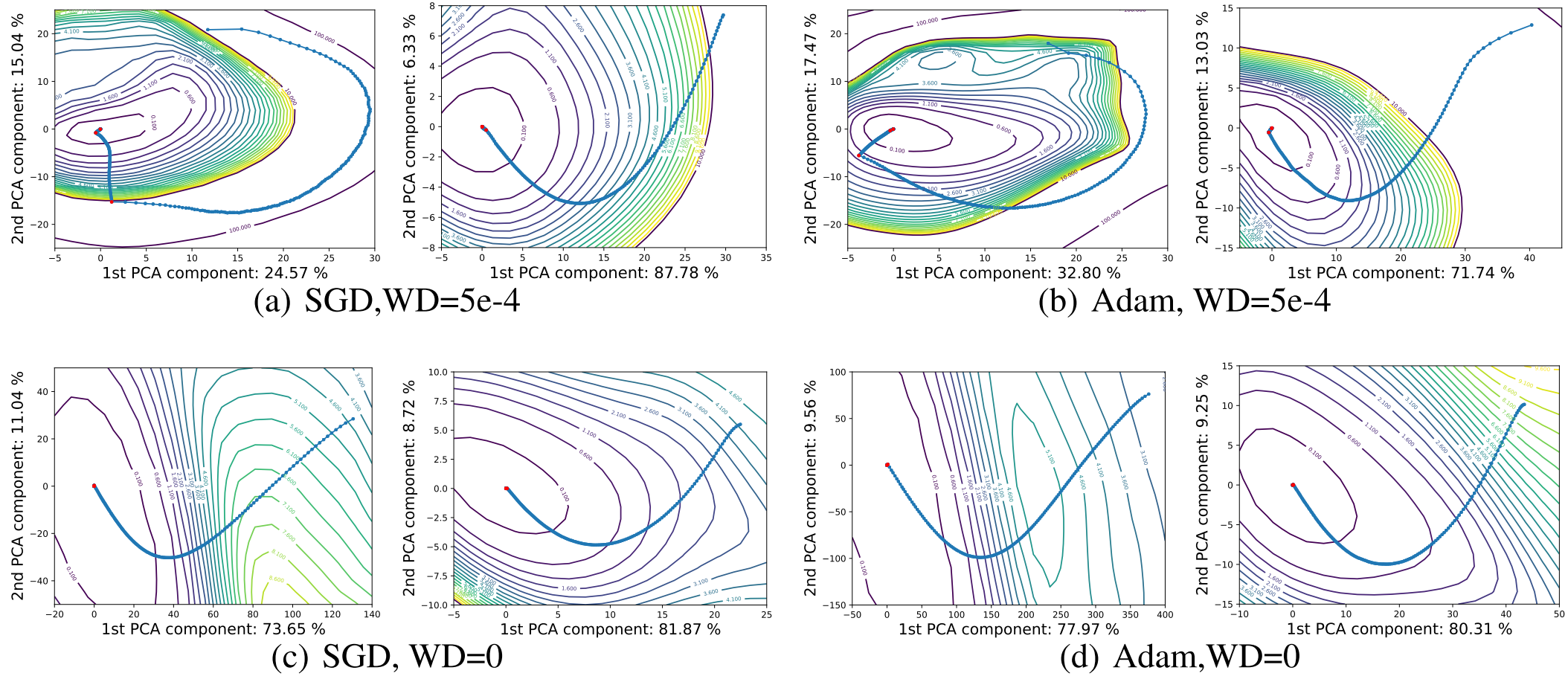
빨간 점은 Learning Rate를 줄여 준 지점이다. 각 축의 숫자들은 각 주성분들이 잡아낸 Variation을 나타낸다.

확연히 이전 시각화보다 많은 Variation을 잡아냈고, 각 경로들이 일관된 몇몇 특징들을 보여준다. 학습 초기에는 다 등고선에 수직으로 진행하고 WD를 쓰거나 Small Batch를 쓰면 Stochasticity가 두드러진다. 그리고 공통적으로 LR을 작게하면 현 지점에서 가장 가까운 Minima로 도착 하는 것을 볼 수 있다.

Stochasticity가 두드러져 최적화 과정에서 잡음을 유발하고, 경로를 이탈할 확률이 커지며, 큰 LR에서 등고선에 평행으로 움직이거나 궤도를 따라 돈다.

Remarks

왠만하면 필요하다고 생각되는 부분을 빼면 정리할 때 쳐내는데, 정리하다보니 뺄 내용이 없더라. 선대랑 최적화에 배경 지식이 많지 않은 상태로 읽어서 완전히 이해되는건 아니지만, 생각할 거리가 많아서 흥미진진한 논문인듯.