관련 링크 : https://arxiv.org/abs/1412.6550
Architecture : FitNet(2015)
Abstract
네트워크의 깊이는 성능을 향상시키지만, 깊어질수록 non-linear해지므로 gradient-based training은 어려워진다. 본 논문에서는 Knowledge Distillation를 확장시켜 hint라는 개념을 도입해 기존의 네트워크를 이용해 더 좁고 깊은 네트워크를 학습시킨다. 학습된 네트워크는 더 빠르고 좋은 일반화 성능을 보였다.
Knowledge Distillation은 파라미터수가 많고 느린 teacher 네트워크의 출력을 이용해 파라미터수가 적고 빠른 student 네트워크를 학습시키는 방법으로, 뒤에서 자세히 설명한다.
1. Introduction
넓고 깊은 네트워크들은 inderence time에서 매우 느리다는 단점이 있다. 따라서 이를 해결하려는 많은 시도들이 있었다. 처음에는 복잡하고 큰 앙상블 네트워크가 unlabeled 데이터를 label하고, 그렇게 label된 데이터를 작은 네트워크에게 학습시켜 큰 네트워크의 출력을 모방하도록 학습시켰다. 이는 깊고 넓은 네트워크를 얕지만 더 넓은 네트워크로 압축하는데 이용되었다. 최근에는, Knowledge Distillation이란 확장된 방법을 이용해 앙상블 네트워크를 동일한 깊이의 단일 네트워크로 압축시켰다.
하지만 위의 방법들은 깊이가 성능을 향상시킨다는 이점을 이용하지 않았다. 깊이의 이점을 이용하기는 어렵지만, 이를 이용하기 위해 초기에는 네트워크를 한 층씩 학습시켰고, 최근에는 중간층에도 분류기를 달아 전체 네트워크를 학습시키는 방법이 사용되었다. 또, 네트워크에게 쉬운 예시부터 어려운 예시까지 순서대로 보여주며 학습시키는 Curiculum Learning도 연구되었다.
초기에는 다른층은 고정시키고 한층씩 local minima를 찾아가는식으로 학습했지만, local minima의 집합이 global minima일 거라는 가능성은 보장되지 못했다. 이후에는 깊은 네트워크에서 gradient 전달이 약해지는것을 해결하기 위해 중간층에서 backprop하는 방법이 이용되었다.(Googlenet 등)
논문에서는 깊이의 이점을 이용하기위해 복잡한 네트워크(wide and deep)를 좁고 더 깊게 압축시킬것이다. 압축시키는 방법은 KD를 기반으로 삼고, 복잡한 네트워크의 중간층을 이용해 압축된 네트워크의 중간층을 학습시키는 intermediate-level hint를 도입했다. 여러 데이터셋에서 실험한 결과, 압축된 네트워크는 더 적은 파라미터와 연산량을 가지면서 더 좋은 일반화 성능을 보였다.
2. Method
Notation
- 앙상블된 넓은 네트워크를 teacher, 압축된 네트워크를 student라고 정의한다.
- $\mathrm T$는 teacher, $\mathrm S$는 student를 뜻한다.
- $\mathbf a_T$, $\mathbf a_S$는 softmax전의 출력을, $\mathrm {P_T}$,$\mathrm {P_S}$는 sofrmax후의 출력을 뜻한다.
- $\mathbf {W_K}$는 네트워크 $\mathbf K$의 파라미터를 뜻한다.
2.1 Review of Knowledge Distillation
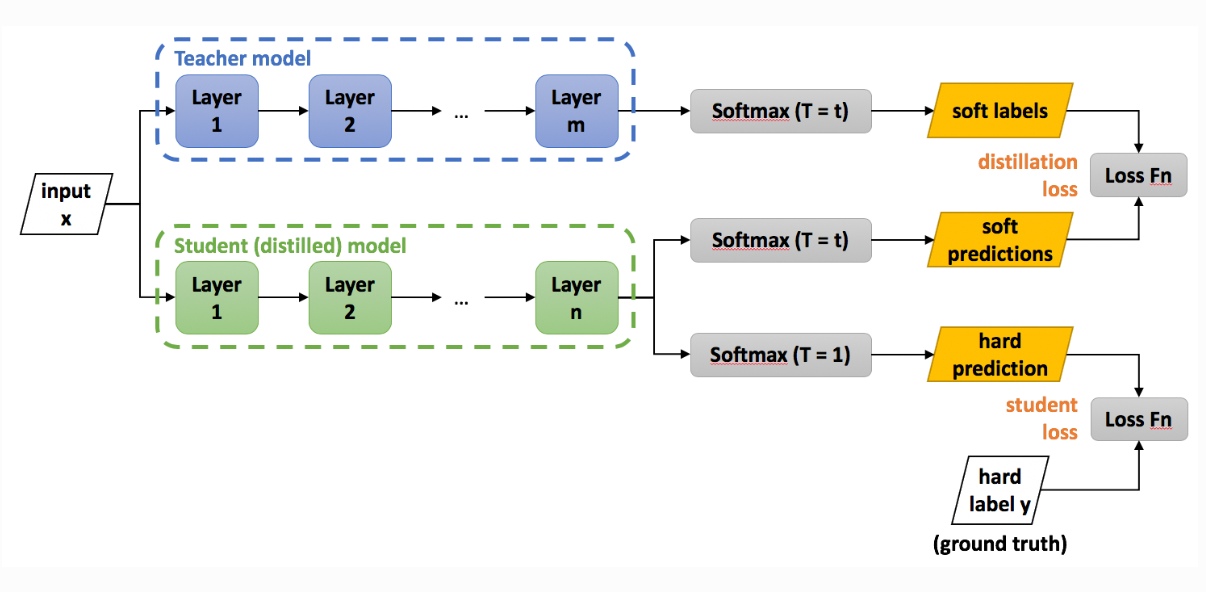
KD는 위의 그림으로 설명된다.
위 그림에서 Teacher는 원래 앙상블 모델이므로, 여러 모델들의 출력을 softmax전에 평균내거나 후에 평균을 내서 사용한다. softmax전에 평균낼때는 기하평균을, 후에 평균낼때는 산술평균을 사용한다.
기하평균은 $\sqrt[n] {a_1, a_2, \cdots, a_n}$을 의미한다. 산술평균과 달리 다양한 특징을 가졌을때 사용한다. 예를들어,
- 카메라 1 : 200화소, 사용자 평점 8점
- 카메라 2 : 250화소, 사용자 평점 6점
을 비교할때 기하평균을 사용하면 각각 40, 38.7이지만 산술평균을 사용하면 104, 128이다.
soft label/prediction과 Loss Fn의 식은 다음과 같다. hard prediction은 (1)식에 $\tau$가 없다.
\[\mathrm {P}^{\tau}_{\mathrm T}=\mathrm {softmax}\left(\mathbf{a}_T \over \tau \right),\quad \mathrm {P}^{\tau}_{\mathrm S}=\mathrm {softmax}\left(\mathbf{a}_S \over \tau \right) \tag 1\] \[\mathcal L_{KD}(\mathbf {W_S})=\mathcal{H}(\mathbf {y_{true}},\mathrm{P_S})+\lambda \mathcal{H}(\mathrm {P}^\tau_{\mathrm T},\mathrm {P}^\tau_{\mathrm S}) \tag 2\]$\tau$는 relaxation으로 1보다 큰 값을 사용하고, $\mathcal H$는 cross-entropy를 뜻한다. $\lambda$는 조절가능한 변수이다. KD는 student가 약간 깊으면 괜찮은 결과를 내놓지만 깊이가 늘어날수록 학습시키기 어렵다.
2.2 Hint-Based Training
hint는 간단히 $\mathrm {T}$의 특정 층 출력으로 정의되고, $\mathrm S$의 특정 층을 guided layer로 정의한 후 hint로 학습시킨다. hint는 regularization의 형태를 띄고 있으므로 over-regularized되지 않도록 hint/guided layer 쌍을 적절히 선택해야한다. $\mathrm T$가 $\mathrm S$보다 넓으므로, 출력의 형태를 맞추기 위한 변환기가 필요하다. 이는 $r$로 정의한다. 파라미터수를 위해 $r$은 conv layer로 사용한다. 전체적인 학습과정은 다음과 같이 표현할 수 있다.
\[\mathcal L_{HT}(\mathbf {W_{Guided}}, \mathbf {W_{r}})=\frac {1}{2}||u_h(\mathbf x; \mathbf{W_{Hint}})-r(v_{g}(\mathbf x;\mathbf {W_{Guided}});\mathbf{W_r})||^2 \tag 3\]$u_h$와 $v_g$는 각각 hint/guided layer까지의 함수를 뜻한다. 주의할 점은 비교를 위해 $u_h$와 $r$의 non-linearity는 같아야한다.
$r$가 FCL일 경우, $\mathrm S$와 $\mathrm T$가 convolution일때, 파라미터수는 $\mathrm W_h \times\mathrm H_h \times\mathrm C_h \times\mathrm W_g \times\mathrm H_g \times \mathrm C_g$이다. $r$을 Conv로 바꾸면, $\mathrm W_k \times \mathrm H_k \times \mathrm C_h \times \mathrm C_g$로 줄어든다. 커널 사이즈는 $h-k+1=g$을 이용해 간단히 구할수 있다.
2.3 FitNet Stage-Wise Training
학습 순서는 다음과 같다.
- $\mathrm T$를 학습시키고, $\mathrm S$의 $\mathbf {W_S}$를 무작위로 초기화한다.
- $\mathrm S$의 guided layer위에 $r$을 붙여서 $\mathcal L_{HT}$을 이용해 $\mathbf {W_{Guided}}$, $\mathbf {W_{r}}$를 학습시킨다.
- $\mathcal L_{KD}$를 이용해 $\mathbf {W_{S}}$를 학습시킨다.
그림으로는 아래와 같다.
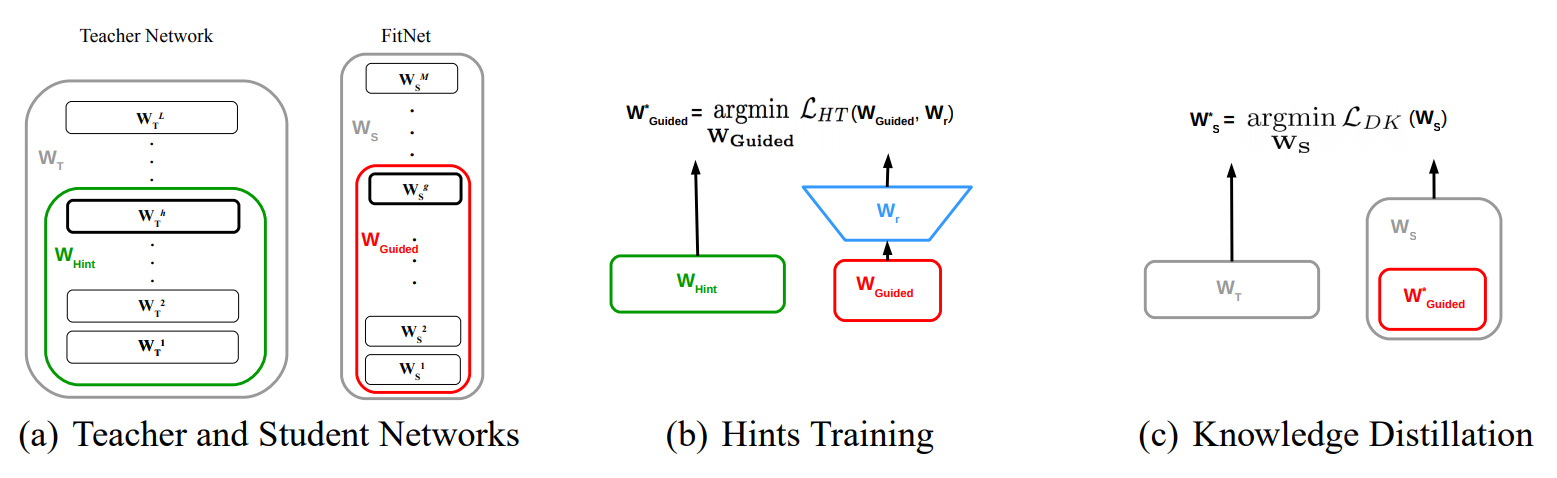
2.4 Relation to Curriculum Learning
CL은 쉬운 예시에서 점점 어려운 예시를 보여주지만, 이 어려움의 정도를 사람이 직접 정의해야하고, CL의 확장 연구에서 도입한 guidance hint도 end-task에 대한 사전지식이 필요하다. 따라서, problem-specific하다.
Problem-specific하다는 말은 풀어야할 문제에 따라 달라진다는 의미로 추측된다. Hint-based learning의 경우에는 데이터셋과 문제가 무엇인지와는 상관없이 teacher만 정의된다면 teacher를 보고 학습할수 있지만 CL은 그렇지 않음을 뜻하는 것 같다.
Hint-based learning with KD는 이 문제를 어느정도 해결한다. $\mathrm T$의 confidence가 높으면 쉬운 예시, 낮으면 어려운 예시로 기준을 모델이 기준을 정하고, 이를 cross-entropy로 구현해 쉬운 예는 학습에 크게 영향을 주고 어려운 예시는 적게 영향을 주도록 만들었다.
confidence가 낮다는 말은 각 클래스에 대한 예측 확률이 동일하다는 것을 뜻하므로, 학습시 어려운 예시는 gradient가 작아 영향이 적다.
또 초기에는 teacher의 영향을 받아 쉬운 예시 위주로 학습하다가 나중에는 어려운 예시는 정답($\mathbf {y_{true}}$)을 보고 학습하도록 $\lambda$를 추가해 학습동안 선형적으로 감소시켰다.
3. Results on Benchmark Datasets
이번 장에서는 다양한 데이터셋에서 학습 세부사항과 결과를 보여준다.
3.1 CIFAR-10 and CIFAR-100
CIFAR-10과 CIFAR-100은 32x32 RGB 이미지들로 각각 10, 100개의 클래스가 있다. 모두 훈련용 50k, 테스트용 10k로 구성되었고, contrast normalization, ZCA whitening만 적용시켰다.
ZCA whitening은 간단히 회전 PCA로 기존 PCA가 가장 큰 고유값을 가지는 고유벡터로 분포를 정사영 시켜서 고유벡터를 축으로 가지는 새로운 분포에서 기존 분포의 위치가 달라졌다면, ZCA는 PCA한 후 이를 회전시켜서 기존 분포와 위치를 같게 해준다는 차이가 있다.
Original PCA ZCA )
CIFAR-10
$\mathrm T$로는 Maxout Network를 사용했고, $\mathrm S$로는 $\mathrm T$의 1/3 파라미터만 가지도록 17 maxout conv layer와 maxout FCL, softmax layer로 구성했다. $\mathrm S$의 11번째 층을 guided layer로, $\mathrm T$의 2번째 층을 hinted layer로 정하고, 학습시 random flipping만 data augmentation으로 사용했다.
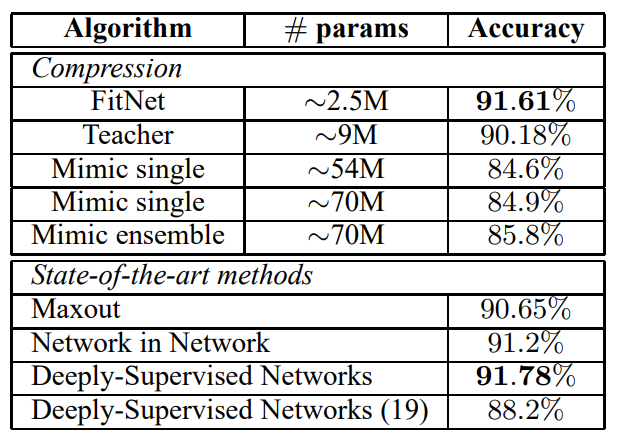
CIFAR-100
실험 방법은 CIFAR-10과 동일하다.

3.2 SVHN
SVHN 데이터셋은 GoogleStreet View로 수집된 House number로, 32x32 RGB 이미지다. 훈련용 73,257개, 테스트용 26,032개, 그리고 추가로 531,131개의 이미지가 있다. $\mathrm T$로는 Maxout Network를 사용했고, $\mathrm S$는 11 maxout conv layer와 FCL, softmax로 구성했다.
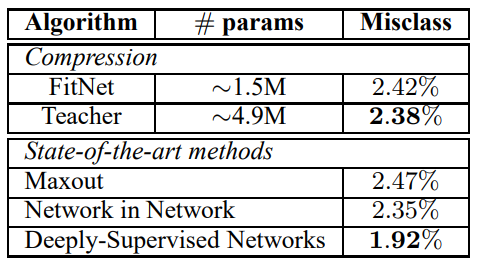
3.3 MNIST
훈련용 60k, 테스트용 10k의 28x28 greyscale 이미지인 MNIST 데이터셋에서 실험을 진행했다. $\mathrm T$는 Maxout Network를 사용했고, $\mathrm S$는 깊이는 두배로 늘리고 파라미터수는 8%로 줄여셔 구성했다. $\mathrm S$의 4번째 층을 guided layer, $\mathrm T$의 2번째 층을 hint layer로 정하고 hint가 실제로 학습에 도움이 되는지 비교하기 위해
- $\mathbf {y_{true}}$를 이용한 평범한 backprop
- Knowledge Distillation
- Hint-based Training
를 비교했다.
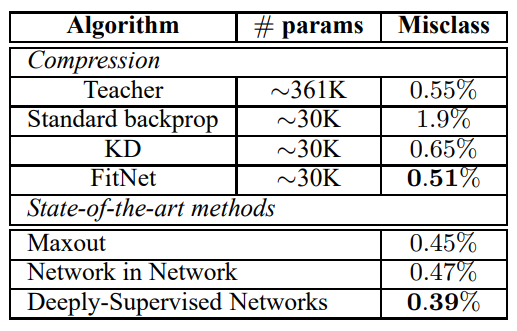
3.4 AFLW
AFLW는 실제 얼굴 사진으로, 25k의 이미지들로 이루어져있다. 얼굴인식을 위해 positive sample로 얼굴부분을 16x16으로 25k 뽑았고, negative sample은 ImageNet 데이터셋에서 얼굴이 없는 부분을 16x16으로 25k 뽑았다.
$\mathrm T$는 ReLU를 가진 3개의 conv layer와 sigmoid layer로를 사용했다. 다양한 구조에서 결과를 확인하기 위해, $\mathrm S$는 두개로, Fitnet 1은 $\mathrm T$보다 15배 적은 연산량을 가지도록, Fitnet 2는 2.5배 적은 연산량을 가지도록 설계했다. 둘 다 7개의 conv layer와 sigmoid layer로 구성되었다.
결과적으로, $\mathrm T$는 4.21%의 오류를 보였고, Fitnet 1은 KD로만 학습했을때 4.58%, HT도 사용했을때 2.55%를 보였다. Fitnet 2는 KD로만 학습했을때 1.95%, HT도 사용했을때 1.85%를 보였다. 이는 hint의 사용이 좁은 네트워크를 학습시키는데 효과가 좋다는것을 보여준다.
4. Analysis of Empirical Results
이 장에서는 HT의 영향을 확인하기 위해 고정된 연산량을 가진 여러 구조를 각각 평범한 backprop, KD, HT로 학습시키고 결과를 비교할것이다. 실험은 CIFAR-10 데이터셋으로 수행했고, 고정된 연산량을 위해 층이 깊어지면 conv layer의 채널수를 줄였다.
4.1 Assisting the Training of Deep Networks
실험에서 각각 30M, 107M의 연산량 제한을 가진 구조들로 실험을 진행한다. 이 연산량은 forward propagation시 필요한 연산량을 기준으로 했다. 결과는 다음과 같다.
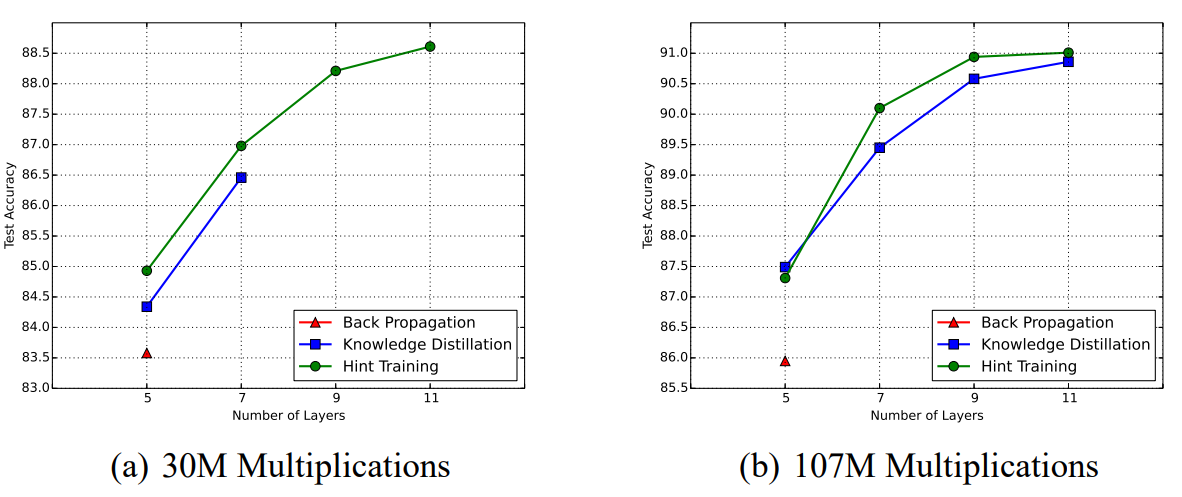
결과를 보면, KD는 층이 깊어지면 학습이 불가능한 반면 HT는 가능하다. 이는 local minima와 saddle point가 많은 깊은 네트워크의 parameter space에서 random initialization으로 좋은 시작점을 찾기가 어렵기 때문이다. 또한 HT가 일반화 성능이 더 좋은것은 HT가 일종의 regularizer로 작용하기 때문이다.
요약하면,
- HT가 KD보다 깊은 네트워크를 잘 학습시킨다.
- 같은 연산량을 가진 네트워크의 경우, 깊을수록 성능이 좋다.
4.2 Trade-Off Between Model Performance And Efficiency

속도와 성능사이에 Trade-off 관계가 있지만, 둘 다 $\mathrm T$보다 향상 시킬 수 있다.
5. Conclusion
intermeidate-level hint를 도입해서 넓고 깊은 네트워크를 좁고 더 깊은 네트워크로 압축시켰다. 이 과정에서 파라미터 수는 줄어들고, 일반화 성능을 좋아졌으며, inference시 더 빨라졌다.


Leave a comment