관련 링크 : https://arxiv.org/abs/1805.01978
Self-supervised Learning : NPID(2018)
Abstract
라벨을 가진 데이터로 학습된 신경망 분류기는 다른 카테고리들 사이의 시각적 유사성을 잘 잡아낸다.
Top-5 Error를 보면 시각적으로 유사한 사진들이 많다.
따라서 본 논문은 이를 확장해 feature들이 instance에따라 구별되기만 하면, class 대신에 instance사이의 시각적 유사성을 포착하는 feature representation을 학습 할 수 있다고 가정한다.
본 논문은 위의 가정을 이용해 기존의 class-level classification을 instance-level non-parametric classification problem으로 구체화 시키고, 많은 instance classes에 의한 계산량 문제를 해결하기 위해 noise contrastive estimation을 사용한다.
1. Introduction

Supervised learning에서 top-5 error가 top-1 error보다 상당히 낮고, top-5의 두 번째 class는 정답과 시각적으로 연관되있을 가능성이 높다. 이는 supervised learning은 추가적인 명령 없이도 자동적으로 semantic categories사이의 유사점들을 찾을 수 있음을 나타낸다. 즉, 이런 유사성은 semantic annotation에서 배우는 것이 아니라 visual data 그 자체로부터 배운다.
서로 연관성이 높은 카테고리들을 묶어서 별도의 신호로 모델에게 알려주지 않아도 모델은 이를 구분 할 수 있다. 이는 annotation을 통해서 상관관계를 배운것이 아니라 이미지 그 자체에서 배웠다는 것을 의미한다. 논문은 이런 맥락에서 아이디어를 가져온 것 같다.
그렇다면 이를 확장해서, class가 아닌 instance별로 유사성을 가지는 representation을 배우도록 하면 어떨까? class를 supervision으로 줬을때 처럼 instance사이의 유사점을 배울 수 있을 것이다. 하지만 이 경우 class의 수는 전체 학습 데이터셋의 크기와 같아지고, softmax를 그만큼 늘리는 것은 계산량의 관점에서 불가능하다. 따라서 이를 해결하기 위해 Noise Contrative Estimation를 사용하고 Proximal Regularization를 이용하여 학습을 안정화한다.
또한 기존의 unsupervised method는 training task에서 학습된 feature들이 unkown testing task에서 linearly separable하다고 가정하고 SVM을 이용해 이미지를 분류했다. 하지만 실제로 linearly separable한가는 명확하지 않다.
본 논문은 이를 개선하기 위해 Non-Parametric approach를 이용해 training과 testing을 consistent하게 만든다. 두 과정이 consistent하면 training task와 testing task의 feature들이 같은 space를 이용하므로 동일한 metric을 이용 할 수 있다. 이때 SVM보다 데이터 본연의 특징과 학습된 feature의 성능을 더 잘 나타낼 수 있도록 kNN 분류기를 사용한다.
최종적으로 본 논문의 모델은 다음의 특징을 갖는다,
- 학습 데이터가 많아지거나 사용된 모델의 성능이 좋을수록 분류 성능이 증가한다.
- Non-parametric approach로 인해 모델이 compact하다.
2. Related Works
- Generative Models : RBM, VAE, GAN
- Self-supervised learning : context prediction, Counting, context/colorization AE
- Metric Learning : 입력 데이터들이 얼마나 유사한지를 측정하는 metric을 학습
- Examplar CNN : 논문의 방법과 유사하지만 parametric paradigm을 사용
3. Approach
논문의 목적은 supervision 없이 이미지 $x$를 feature $v$에 mapping하는 딥뉴럴넷 $v=f_\theta(x)$를 학습하는 것이다. 잘 학습된 경우 $f_\theta$의해 만들어진 $v$는 metric $d_\theta(x,y)=\|f_\theta(x)-f_\theta(y)\|$이 적용되는 공간상에 존재한다.
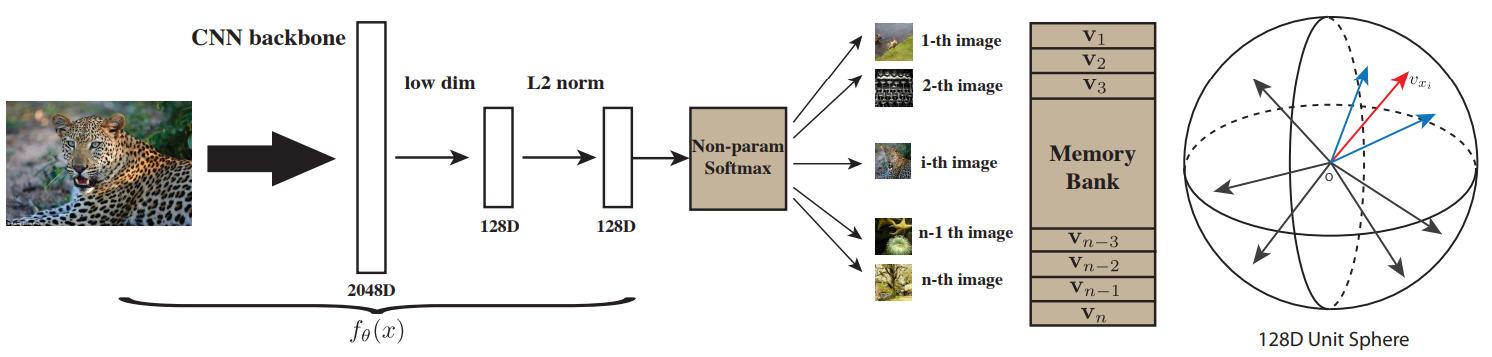
전체 과정을 요악한 그림이다. 최종적인 128D Unit Sphere는 위에서 언급한 metric이 적용된다. 여기서 metric이란 공간의 점들의 경우 거리, 벡터들의 경우 내적으로 가까움이나 유사함을 나타내는 방법을 의미한다. 예를들어 점들은 가까우면 거리라는 metric의 값이 작고, 벡터가 유사하면 내적이라는 metric이 커진다.
3.1 Non-Parametric Softmax Classifier
Instance-level classification이므로, 데이터셋의 크기가 $n$이라면 $n$개의 classification task를 수행한다.
Parametric Classifier : 이미지 $x$의 feature $v$가 $i$번째 클래스로 인식될 확률은 다음과 같다.
\(P(i|\mathrm{v})=\frac {\exp(\mathrm w_i^T \mathrm v)}{\sum^n_{j=1}\exp(\mathrm w_j^T \mathrm v)} \tag 1\)
- $\mathrm{v_1, \ldots,v_n}$ : 입력이 $x_1,\ldots,x_n$일때 feature $v_i=f_\theta(x_i)$
- $w_i$ : $i$번째 이미지일때 계산되는 weight vector
Non-Parametric Classifier : Parametric Classifier의 문제는 $w$가 class의 초기 위치를 지정해 instance간의 비교를 방해한다는 것이다. 따라서 이를 보완하여 식 (1)을 다음과 같이 바꾼다.
\(P(i|\mathrm{v})=\frac {\exp(\mathrm v_i^T \mathrm v/\tau)}{\sum^n_{j=1}\exp(\mathrm v_j^T \mathrm v/\tau)} \tag 2\)
- $|\mathrm v |=1$이 되도록 L2-normalization을 수행한다.
- $\tau$ : temparature parameter로 unit sphere에서 $\mathrm v$의 concentration에 영향을 준다.
최종적인 학습 목표는 joint probability $\prod^n_{i=1}P_\theta(i|f_\theta(x_i))$를 최대화 시키는 것으로, 이는 negative log-likelihood를 최소화하는 것과 동일하다.
\[J(\theta)=-\sum_{i=1}^n\log P(i|f_\theta(x_i)) \tag 3\]Learning with A Memory Bank : 식 (2)의 계산을 위해서는 모든 이미지의 feature $\mathrm v$가 필요하다. 따라서 제일 처음에는 unit random vector로 초기화하여 memory bank $V$에 저장하고, 이후 각 learning iteration마다 $\theta$와 함께 업데이트 한다.
SGD를 사용하므로 한 번에 하나의 이미지만 입력으로 들어오고, 입력에 해당하는 $V$안의 $v$를 업데이트한다.
따라서 식 (2)는 다음과 같이 바뀐다. \(P(i|\mathrm{v})=\frac {\exp(\mathrm v_i^T \mathrm f_i/\tau)}{Z_i} \tag 4\)
-
Normalizing constant $Z_i$ : \(Z_i=\sum^n_{j=1}\exp(\mathrm v_j^T \mathrm f_i/\tau)\tag 5\)
- $f_i$는 동일한 iteration에서 계산된 것, $\mathrm v_i$는 $V$에서 가져온 것이다.
Discussions : 기존의 $\mathrm w_j$를 $\mathrm v_j$로 대체하여 두 가지 장점을 얻을 수 있다.
-
모델이 특정 class가 아니라 feature representation과 그에 따른 metric을 학습하면서 새로운 class에도 잘 적용된다.
모델이 annotation이 아닌 데이터 위주로 학습하므로 새로운 annotation을 가진 데이터를 입력으로 받아도 feature representation을 계산해 시각적으로 유사한 데이터들을 판단할 수 있다는 의미인 듯
-
$\mathrm w$의 gradient를 계산할 필요가 없다.
3.2 Noise-Contrastive Estimation
식 (3)을 계산하기 위해 식 (2)를 계산 할 때, 이미지의 수가 많아지면 계산이 불가능해진다. 동일한 문제가 Word Embedding에서도 발생했고, 세 가지 방법을 이용해 해결했다.
-
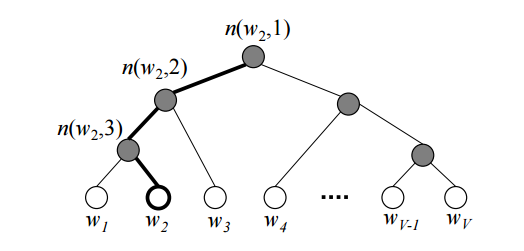
Hierarchical Softmax: 각 단어들을 leaves로 가지는 binary tree를 하나 만들고, 해당하는 단어의 확률을 계산할 때 root에서부터 해당 leaf로 가는 길을 따라 확률을 곱해 해당 단어가 나올 최종적인 확률을 계산한다.
자세한 설명은 위 그림 클릭
- Negative Sampling : 모든 단어들에 대해 Softmax를 수행하므로 계산량이 많아지는 것을 개선하기 위해 해당하는 단어와 그렇지 않은 일정 개수의 Negative Sample에 대해 Softmax를 수행한다.
- Noise-Contrastive Estimation : multi-class classification을 data sample인지 noise sample인지 판단하는 binary classification으로 바꾼다.
본 논문에서는 NCE를 사용한다. feature $v$를 가지는 입력 $i$가 data sample일 posterior probability은 다음과 같다. \(h(i, \mathrm v):= P(D=1|i,\mathrm v)=\frac {P(i|\mathrm v)}{P(i|\mathrm v)+mP_n(i)}\tag 6\)
- $P_n = 1/n$ : noise distribution
- $mP_n$ : noise sample이 data sample보다 $m$배 더 많다고 가정
따라서 학습 목표는 negative log-posterior distribution를 최소화 하는 것으로 바뀐다.
\(J_{NCE}(\theta)=-\mathbb E_{P_d}[\log h(i,\mathrm v)]-m\cdot\mathbb E_{P_n}[\log (1-h(i,\mathrm {v'}))] \tag 7\)
- $P_d$ : actual data distribution
- $\mathrm {v’}$ : $P_n$에서 무작위로 sampling된 이미지들의 representation
또 식 (4)의 $Z_i$의 계산량이 여전히 많으므로 이를 Monte Carlo 근사를 이용해 계산량을 줄인다.
\(Z\simeq Z_i \simeq n\mathbb E_j[\exp(\mathrm v^T_j \mathrm f_i /\tau)]=\frac {n} {m}\sum^m_{k=1}\exp(\mathrm v^T_{j_k} \mathrm f_i /\tau) \tag 8\)
- $\{j_k\}$ : 무작위 인덱스의 집합
- $V$가 계산되지 않은 첫번째 iteration에도 근사가 유효했다.
결과적으로, NCE를 사용해 각 샘플당 복잡도를 $O(n)$에서 $O(1)$로 줄일 수 있다.
3.3 Proximal Regularization
일반적인 classification과 달리 본 논문은 한 class당 하나의 이미지만 가지고 학습한다. 따라서 각 epoch당 각 class는 한 번만 학습되고 매번 loss가 크게 진동한다. 이를 완화하기 위해 regularization term을 추가한다. \(J_{NCE}(\theta)=-\mathbb E_{P_d}[\log h(i,\mathrm v_i^{ (t-1)})-\lambda\|\mathrm v_i^{(t)}-\mathrm v_i^{(t-1)}\|^2_2]-m\cdot\mathbb E_{P_n}[\log (1-h(i,\mathrm {v'^{(t-1)}}))] \tag {10}\)
- iteration $t$일때 feature representation은 $\mathrm v_i^{(t)}$이고, $V$에는 $\mathrm v^{(t-1)}$이 들어있다.
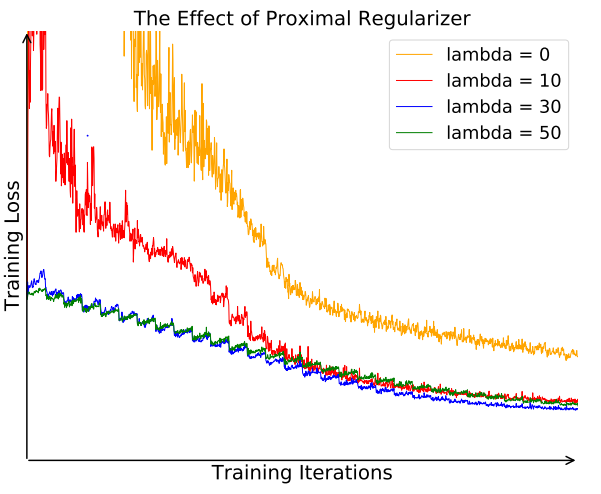
Regularization을 적용한 경우 진동 폭이 작고 학습이 안정적이다.
3.4 Weighted k-Nearest Neighbor Classifier
테스트 이미지 $\hat x$를 분류하기 위해서 여러 단계를 거친다.
- $\mathrm {\hat f}=f_\theta(\hat x)$를 계산하고 $V$안의 모든 $\mathrm v$와 cosine similarity $s_i=\cos(\mathrm v_i, \mathrm{\hat f})$를 계산한다.
- 가장 가까운 $k$개의 nearest neighbors를 선택해 $\mathcal N_k$라고 명명한다. 논문에서는 $k=200$을 사용한다.
- Countributing weight $\alpha_i=\exp(s_i/\tau)$를 계산한다. 논문에서는 $\tau = 0.07$을 사용한다.
- 클래스 $c$별로 $w_c=\sum_{i\in\mathcal N_k}\alpha_i\cdot 1(c_i=c)$를 계산해 가장 높은 class로 분류한다.
4. Experiments
4.1 Parametric vs. Non-parametric Softmax
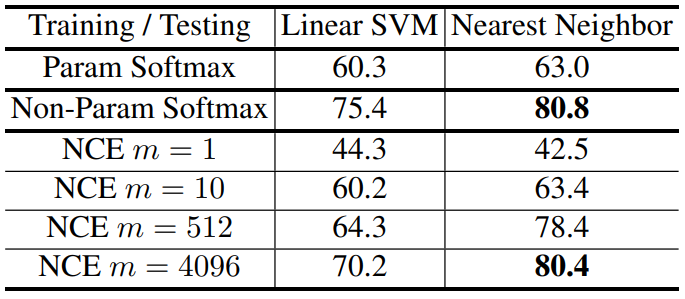
- CIFAR-10 데이터셋과 ResNet-18을 이용한다. 충분히 작은 데이터셋이므로 여러 근사방법을 사용하지 않은 식 (2)로 학습했다.
- SVM은 학습된 ResNet-18의 feature를 이용해 학습하여 SVM의 feature로 분류를 수행하지만 kNN 분류기는 오직 ResNet-18의 feature로만 분류를 수행하므로 representation의 quality를 더 잘 반영한다.
- $m$값이 커짐에 따라 성능이 증가하고, $m=4096$일때의 성능은 근사하지 않았을때의 성능에 다가간다. 따라서 NCE에서 사용된 근사는 유효하다.
4.2 Image Classification
Experimental Settings
- Hyper-Parameter : $\tau = 0.07$, $m=4$
- SGD with momentum
- Batch size : $256$, Training epochs : $200$
- LR scheduler : 120 epochs까지 $0.03$, 이후 40 epochs당 $1/10$
Comparisons 다양한 method들과 두 가지 방식으로 성능을 비교한다.
- $\mathrm {conv1}$에서 $\mathrm {conv5}$까지 각 층에 linear SVM을 추가해 성능을 평가한다.
- 최종 출력에 kNN 분류기를 추가해 성능을 평가한다.
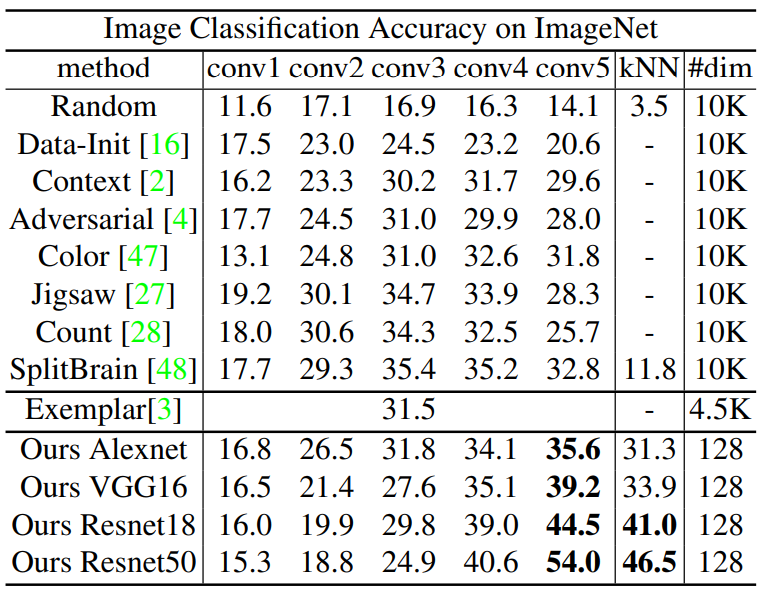
Top-1 acc on ImageNet, 다른 Method들은 모두 backbone network로 ResNet-101을 사용했다.
- 논문의 방법은 쉽게 더 큰 network에서 이용가능하고 더 좋은 성능을 보인다.
-
다른 방법들에 비해 kNN 분류기를 사용해도 linear SVM과 큰 성능차이가 발생하지 않았다. 이는 좋은 metric이 학습 되었음을 의미한다.
-
다른 방법들은 $\mathrm {conv3}$에서 $\mathrm {conv4}$로 바꾸면 성능이 하락했지만, 본 논문의 방법은 오히려 증가했다. 중간층의 feature들의 차원($10,000$)은 마지막층($128$)보다 크기 때문에 논문의 방법의 계산 비용이 효율적이다.
1.28M의 encoded feature의 크기가 600MB밖에 안된다.
Feature generalization
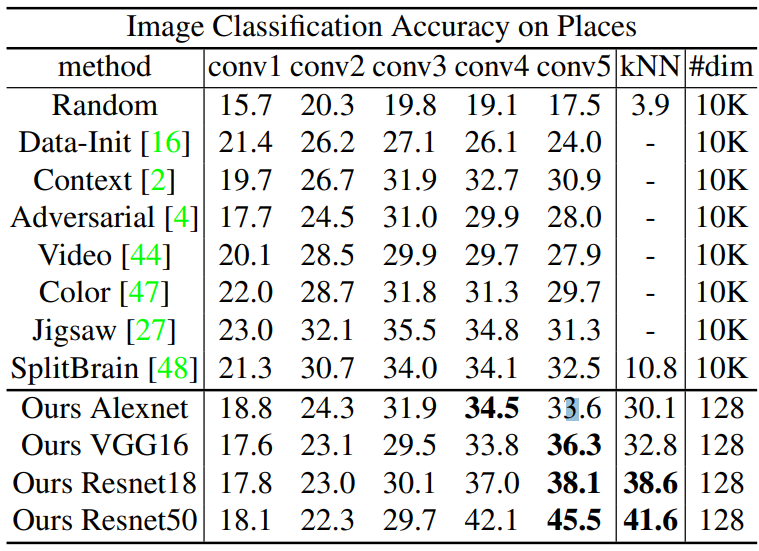
Top-1 acc on Places, finetuning없이 일반화 성능을 평가한다.
- 다른 방법들에 비해 상당히 좋은 성능을 보인다.
Consistency of training and testing objectives
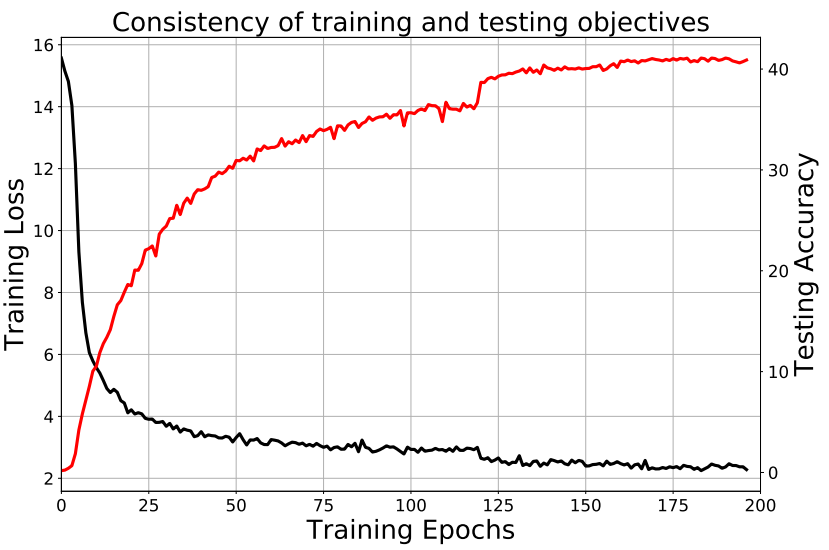
- Training task의 성능과 Testing accuracy 비례한다. 이는 유사성을 인식하도록 ㅓ
- Traning obtjective와 Testing objectve를 consistent하게 설계하면 더 좋은 성능을 이끌어 낼 수 있다.
The embedding feature size

ResNet-18에서 성능을 비교했다.
Training set size

ResNet-18에서 성능을 비교했다.
Qualitative case study

위 4행은 query와 동일한 class를 가진 사진들중 가장 가까운 10개, 아래는 가장 먼 10개이다.
- 가장 먼 경우도 어느정도 시각적 유사성을 가진다.
4.3 Semi-supervised Learning
Semi-supervised learning은 적은 수의 labeled 데이터와 많은 unlabeled 데이터를 가지고 있을때 사용하는 방법이다. ImageNet 데이터셋의 일부를 labeled 데이터로 사용해서 실험을 진행한다. Experimental Settings
- Proportion of Labeled Data : $1\%, 2\%, 4\%, 10\%, 20\%$
- Finetuning on Labeled Data
- Training epochs : $70$
- LR scheduler : 초기값은 $0.01$, 이후 30 epochs당 $1/10$
Results
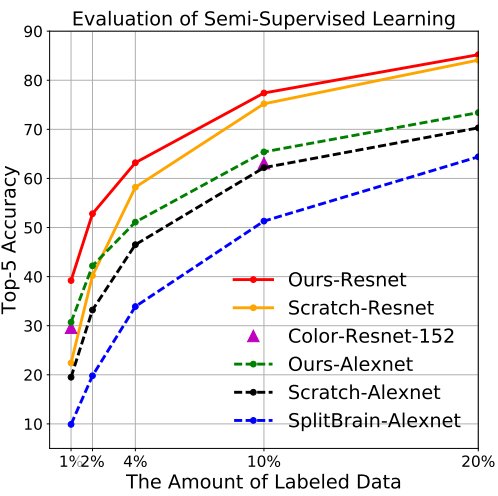
Scratch-Resnet은 Supervised method이다.
4.4 Object Detection
PASCAL VOC 2007 데이터 셋을 이용해 detection에서 일반화 성능을 평가한다. AlexNet과 VGG16을 사용할때는 Fast R-CNN, ResNet을 사용 할때는 Faster R-CNN에 fine-tuning 했다. 기존 관행과 동일하게 AlexNet, VGG16을 finetuning할때는 $\mathrm {conv1}$를 fix했고, ResNet은 $\mathrm {ResBlock1}$부터 $\mathrm {ResBlock3}$까지, 그리고 모든 $\mathrm {BN}$을 fix했다.
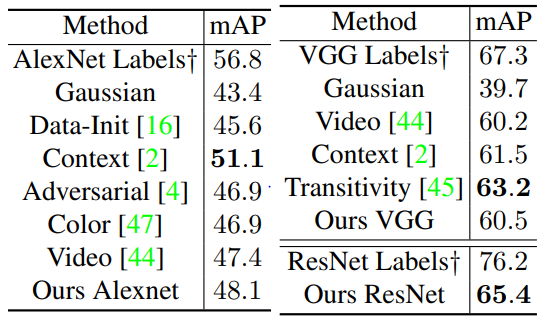
$\dagger$는 supervised pretraining method를 의미한다.
5. Summary
- 본 논문은 non-parametric softmax를 이용하여 instances간의 distinction을 최대화 하는 unsupervised method를 제안한다.
- 기존 방법들에 비해 compact하고, 데이터가 많고 깊은 네트워크를 사용하면 성능이 향상된다.
- 괜찮은 일반화 성능을 보인다.
Leave a comment