관련 링크 : https://arxiv.org/abs/1708.03888
Training : LARS(2017)
Abstract
큰 배치(batch)로 모델을 학습시키면 학습 시간을 짧아지지만 모델의 성능이 저하된다. 본 논문에서는 이를 극복하기 위한 방법인 LARS(Layer-wise Adaptive Rate Scaling)를 제안한다. 이를 이용해 Alexnet은 8K, Resnet-50은 32K의 배치로 성능 저하 없이 모델을 학습시켰다.
1. Introduction
큰 모델은 학습시간이 길다. 이를 해결하기 위해 더 많은 GPU를 사용한다. 하지만 이 경우 각 GPU가 처리해야 할 미니배치의 크기는 어느정도 커야하고 따라서 GPU를 추가할때마다 배치의 크기도 커진다. 하지만 큰 배치를 사용하는 것은 모델의 성능에 악영향을 끼친다.
일반적으로 큰 배치를 사용하면 작은 배치를 사용할때보다 epoch당 iteration이 더 적고, 따라서 이를 어느정도 보완하기 위해 더 큰 LR(learning rate)를 사용한다. 하지만 큰 LR을 이용하면 학습이 어려워지고, 초기 단계에서 모델이 발산해버린다. 따라서 초기 단계에서는 작은 LR을 사용하고, 몇 epoch동안에 linear scaling하는 linear scaling LR with warm-up 방법이 사용되었다. 하지만 여전히 배치가 크면 높은 LR 때문에 학습이 제대로 이루어지지 않았다.
LR warm-up : lr이 $p$일때 warm-up을 $n$ epoch동안 한다면, 첫 번째 iteration에서 lr은 $1\times p/n$, 두 번째는 $2 \times p/n$를 사용한다.
본 논문에서는 LR이 클때 학습 안정성을 분석하기 위해 weights와 gradients update의 norm사이의 비율을 측정했고, 이 비율이 작으면 학습이 불안정하고 크면 학습이 이루어지지 않음을 발견했다. 따라서, 이를 이용한 Layer-wise Adaptive Rate Scaling을 제안한다. 이는 ADAM이나 RMSProp과 유사한 adaptive algorithm이지만 두 가지 차이점이 있다.
- Weight가 아닌 Layer마다 LR을 다르게 사용한다.
- Update되는 정도가 Weight Norm에 따라 달라진다.
2. Background
First Background
Stochastic Gradient based method는 다음의 방식으로 weight를 update한다.
\[w_{t+1}=w_t - \lambda \frac {1}{B}\sum^B_{i=1}\nabla L(x_i, w_t) \tag 1\]- $B$ : 배치 크기, $t$ : 반복 횟수
- GPU $N$개로 학습시킬때는 각 GPU에 $\frac B N$의 미니 배치가 할당되고, 모든 GPU가 계산을 완료하면 업데이트된다.
$B$가 커질때는 Linear LR scaling 방식을 이용한다.
\[w_{t+1}=w_t - \lambda_2 \frac {1}{B_2}\sum^{B_2}_{i=1}\nabla L(x_i, w_t) \tag 3\]- 이떄 $B_2=2\times B$로 2배 키웠으므로, $\lambda_2 = 2 \times \lambda$도 2배로 키워주는게 Linear LR scaling이다.
기존 방식을 2 iteration 학습시켰을때인 (2)과 위의 (3)을 비교해보면, $\nabla L(x_j, w_{t+1})\approx \nabla L(x_j,w_t)$라 가정했을때 거의 유사함을 알 수 있다.
\[w_{t+2}=w_t - \lambda \frac {1}{B}\left (\sum^B_{i=1}\nabla L(x_i, w_t)+\sum^B_{j=1}\nabla L(x_j, w_{t+1})\right ) \tag 2\]
이 방식은 BN과 함께 사용되어 기존 방식보다 좋은 성능을 이끌어냈다.(물론 BN만 사용했을때도 성능은 향상된다.) 하지만 배치 크기가 더 커질경우 너무 큰 LR 때문에 학습이 불안정했고, 여러 연구에서 GBN(Ghost Batch Normalization)과 Square root scaling 등을 사용해서 개선하려 했지만 여전히 작은 배치를 사용했을때와 동떨어진 성능을 보였다.
GBN : 기존의 BN이 각 배치당 표준편차와 평균을 구해 normalization했다면, GBN은 큰 배치사이즈를 사용할때 그보다 작은 가상의 배치를 만들고 이를 이용해 normalization하는 방법
Square root scaling : $\eta_L=\sqrt{\frac {|B_L|}{|B_S|}}\eta_S$, 큰 배치의 크기와 작은 배치의 크기를 이용해서 LR을 조정하는 방법. $\eta_L$은 큰 배치일때 LR, $\eta_S$는 작은 배치일때 LR이다.
이후 Introduction에서 언급한 LR warm-up과 Linear scaling을 이용해 Resnet-50을 $B=8\mathrm K$에서 의미있는 성능을 보였고, 본 논문은 이 방법을 기초로 발전시킨다.
Second Background
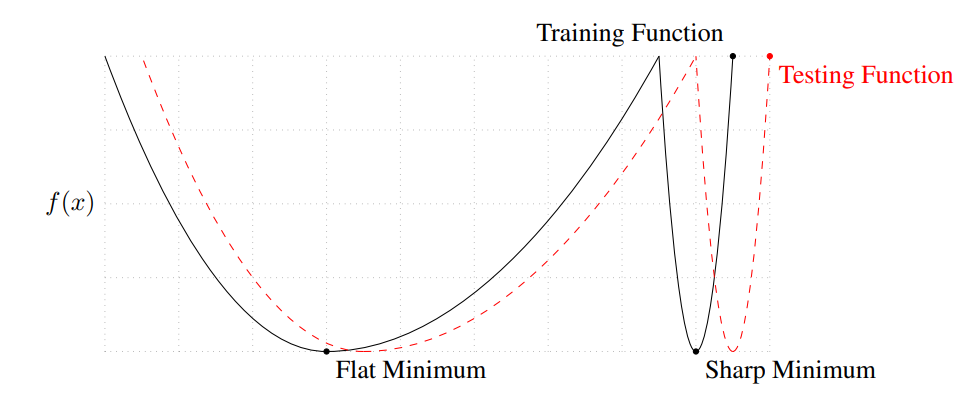
Generalization gap은 큰 배치로 학습할때 작은 배치로 학습한 것 보다 성능이 저하되는 현상을 말한다. 한 연구에서는 큰 배치로 학습시켰을때 training function이 sharp minimizer에 수렴하는 경향이 있음을 밝혔고 이를 해결하려 했지만, 큰 성과는 내지 못 했다.
큰 배치를 사용하면 gradient는 많은 데이터에 의해 계산되어 학습 방향을 바꾸기 어려워 극소값에 빠질 경우 빠져나오기 힘들다. 하지만 작은 배치의 경우 특이한 데이터들에 의해 계산된 gradient가 기존 모델의 학습 방향과 반대되는 방향으로 업데이트해 극소값에서 빠져나올 수 있다.
3. Analysis of Alexnet Training with Large Batch
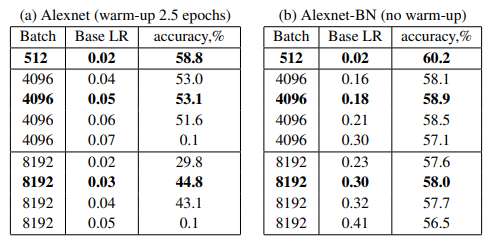
Background에서 언급한것 처럼 BN을 사용했을때가 그렇지 않을때보다 큰 배치를 사용했을때 성능이 더 좋다. 하지만 BN을 사용했을때 여전히 Baseline보다 2%정도의 차이가 존재했고, 이것의 원인이 generalization gap인지 확인하기 위해 $B=256$과 $B=8\mathrm K$의 Loss를 비교했다.
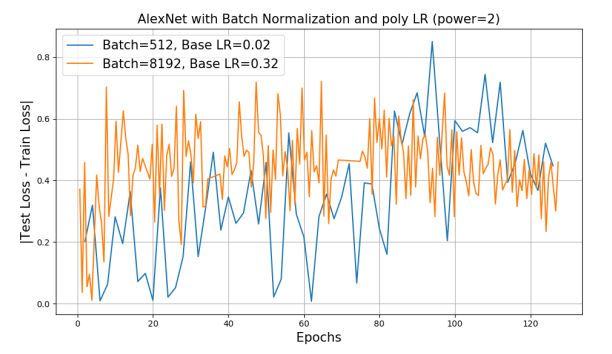
하지만 Loss가 유사한 것으로 보아 성능 저하의 원인이 generalization gap이 아님을 알 수 있다.
4. Layer-wise Adpative Rate Scaling(LARS)
Introduction에서 언급한 것처럼, 본 논문은 weight와 gradient update의 비율인 $\|w\|/\|\lambda \times \nabla L(w_t)\|$가 각 weight와 bias마다, 각 층마다 다르고, 이 비율이 낮으면 학습이 불안정하고 높으면 학습이 느려짐을 발견했다.
기존 SGD는 모든 층에 동일한 LR $\lambda$를 사용해 $w_{t+1}=w_t-\lambda\nabla L(w_t)$를 수행한다. 이때 $\lambda$가 크다면 $\|\lambda \times \nabla L(w_t)\|$가 $\|w\|$보다 커질 수 있고 모델은 발산한다. 따라서 학습 초기에는 LR과 weight initialization이 중요하다.
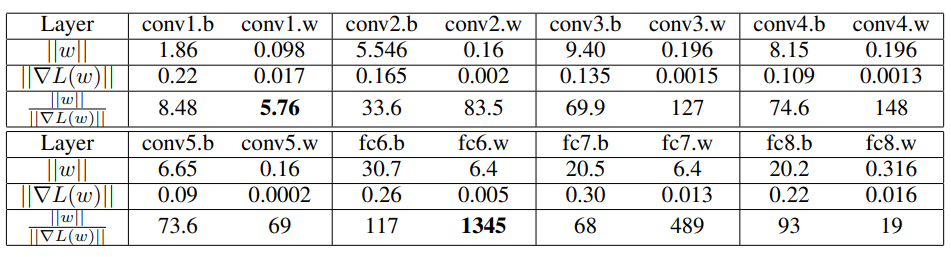
AlexNet-BN의 첫 번째 iteration에서 weight와 gradient의 L2 norm
기존의 warm-up은 모든 층에 작은 LR을 사용해서 이 비율을 낮춰 unstability를 해결했는데, 본 논문은 다른 방법을 사용한다.
-
각 layer $l$에 Local LR $\lambda^l$를 적용한다.
\[\Delta w^l_t = \gamma \times \lambda ^l \times \nabla L(w^l_t) \tag 4\]-
$\gamma$ : global LR
-
\[\lambda ^l = \eta \times \frac {\|w^l\|}{\|\nabla L(w^l)\|+\beta \times \|w^l\|}\tag 6\]
- $\eta$ < 1(trust coefficient) : 한번의 업데이트동안 weights의 변화가 얼마나 믿을만한지 판단하는 계수
- $\beta$ : weight decay를 이용할 때 사용, 사용하지 않는다면 분모의 두 번째 항은 무시한다.
LARS는 업데이트의 정도가 더 이상 gradient의 크기에 의존하지 않게되어 gradient vanishing/exploding을 부분적으로 제거할 수 있다. 또 $\frac {\|w^l\|}{\|\nabla L(w^l)\|}$가 크면 LR을 키우고, 작으면 LR을 줄여서 학습을 원활히 한다는 것이다.

-
이 방법을 사용하면 local LR은 layer와 batch size에 따라 바뀌게 된다.

5. Training with LARS
Alexnet
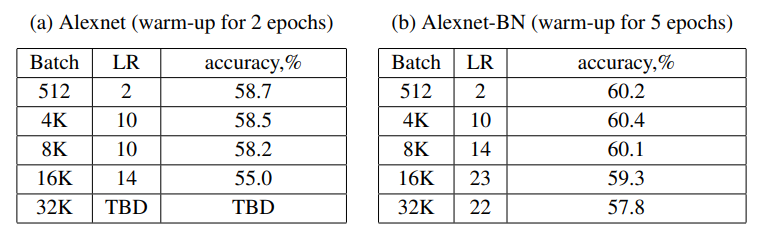
TBD : To Be Determined으로 아직 결정되지 않았지만 추후 결정된다는 의미
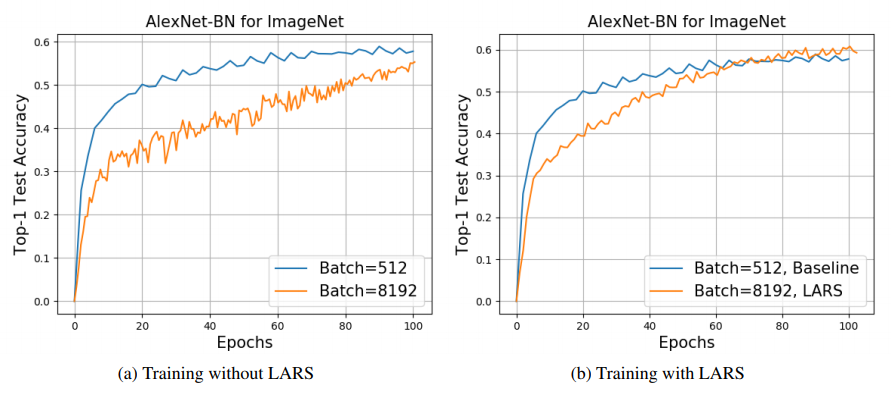
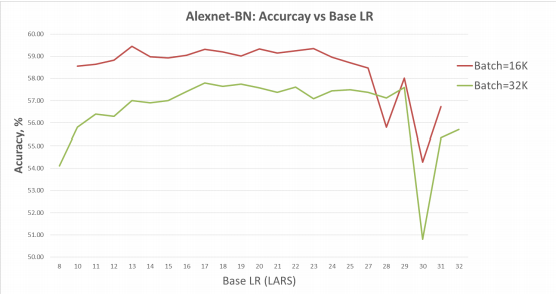
최고 성능을 보이는 base LR의 범위가 꽤 넓음을 볼 수 있다.
ResNet-50
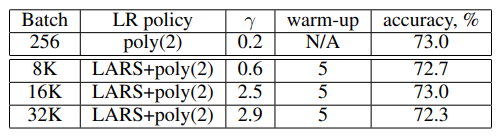
Poly는 Polynomial LR decay를 뜻하고, 5 epoch동안 적용했다.
- $\text {LR}=\text{baseLR}\times(1-\frac {\text{iter}} {\text{maxiter}})^\text{power}$
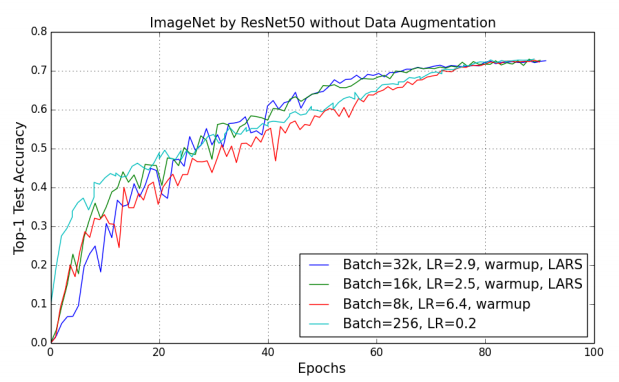
$B=32\mathrm K$로 학습시켰을때 성능이 baseline과 $0.7%$밖에 차이나지 않는다.
6. Large Batch VS Number of Steps
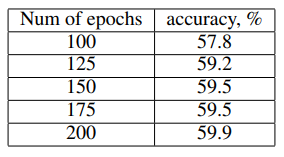
Alexnet-BN, $B=32\mathrm K$
기존 방식들은 100epoch을 기준으로 학습시켰는데, 어떤 방법을 사용해도 baseline에 미치지 못했다. 하지만 학습 epoch을 늘리면 baseline의 성능과 거의 유사해진다. 따라서, 큰 배치를 사용하면 전체 데이터셋의 true gradient와 유사해지므로 추가적인 이득이 있을것 같지만, 작은 배치를 사용했을때와 큰 차이가 없다.
7. Conclusion
- LARS를 이용해 Alexnet과 Resnet-50를 $B=32\mathrm K$로 학습시킬 수 있었다.
- 그 이상의 크기에서의 학습은 아직 해결되지 않았다.

Leave a comment